Тяжелые хвосты и нормальное равенство. Часть 4
@AnarchyPlusКапитал и самоорганизованная критичность
- В прошлых сериях (выпуск 1, выпуск 2, выпуск 3), мы рассказали о том что неравенство в обществе имеет определенный паттерн - паттерн распределений с тяжелыми хвостами (степенные, логнормальные, или смешанные со степенным хвостом). Социальное неравенство — это не просто различие, это характерный паттерн распределения.
- Есть ряд гипотез, почему в обществе возникает неравенство именно такого вида. Им посвящены вторая и третья часть серии.
- В этом тексте, мы обсудим еще одну гипотезу: «самоорганизованную критичность», или СОК.
К сожалению, содержательных моделей СОК для распределения именно капитала практически нет. Тем не менее, об этом часто говорят и попытки создать такие модели делаются — по этим причинам, здесь мы поговорим о концепте в общем смысле, и приведем некоторые спекуляции об отношениях СОК и капитала.
Если вам не интересно читать о моделях самоорганизованной критичности — загляните в конец, к разделу «БЛОК-2: заключение» (https://telegra.ph/critical-power-09-30).
Про ошибки и ляпы сообщайте сюда: @AnarchyGoBot.

Другое объяснение: самоорганизованная критичность
Модели кумулятивного накопления описывают только рост капитала. И никак не учитывают катастрофы. А ведь смерть владельцев, разорение торговых фирм, войны или революции могут вести к перераспределениям богатства на разных масштабах. Как это повлияло бы на паттерн распределения богатства? Как можно объяснить степенные распределения, учитывая катастрофы?
Представьте модели, которые показывают, как степенные распределения возникают благодаря тому что постепенное накопление перемежается быстрыми каскадами перераспределения.
Такие модели есть, и называются моделями «самоорганизующейся критичности».
Критичность
Существует область, в которой степенные распреления давно известны, а а сопутствующее поведение системы — неплохо изучено. Это теория фазовых переходов в физике.
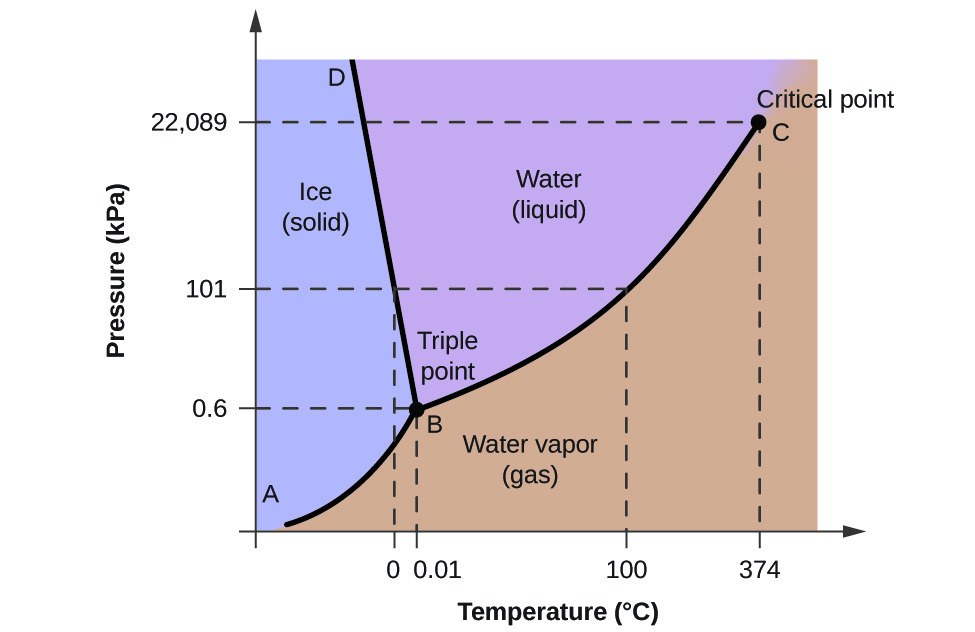
Когда вещество проходит точно через так называемую «критическую точку», наблюдаются особенные явления. Которые также называются «критическими» (critical phenomena). По мере приближения к критической точке, некоторые параметры (как плотность жидкости, концентрация раствора или намагниченность ферромагнетиков), которые называются «параметрами порядка», демонстрируют сильные колебания (флуктуации). Поведение «параметров порядка» вблизи критической точки описывается степенными функциями, а степень функции (та самая переменная «а», знакомая вам из прошлых частей текста) в таком случае называется «критическим индексом» (critical exponent).
С приближением к критической точке, «радиус корреляции» (correlation length) флуктуаций — грубо говоря, это расстояние, на котором изменения в разных участках системы взаимосвязаны — растет, пока не оказывается бесконечно большим в самой критической точке. Это значит, что поведение каждого элемента системы коррелирует с каждым.
Не обязательно вникать в эти детали. Пока стоит отметить три вещи: здесь тоже есть степенные функции; их сопровождают какие-то странные явления; есть модели, которые описывают, как это все происходит.
Гипотеза универсальности и параллели с социальными системами
Для описания «критических явлений» не важно, о каком веществе мы говорим, и какие именно процессы происходят на микро-уровне. У совершенно разных веществ, поведение «параметров порядка» может быть одинаковым. Это происходит, потому что «радиус корреляции» значительно превышает расстояние микро-взаимодействий, и возникающее макро-поведение системы оказывается важнее микроскопических деталей.
Что дает возможность проводить параллели между системами разной природы. Смотря по разным показателям критических индексов (напомним, это степень степенной функции «параметров порядка»), их делят на типы поведения — «классы универсальности»[1]. Предполагается, что критические индексы зависят только от общих черт системы — таких, как размерность пространства и прочих непонятных математических штук.
Теория самоорганизующейся критичности начинается с предположения, что в те или другие классы универсальности можно определить не только вещества в момент фазового перехода, но и системы совсем другого рода, которые показывают похожее поведение каких-либо критических индексов. Скажем, социальные системы, движение тектонических плит и землетрясения, образование рек. Если найти в разных процессах общие критические индексы, их можно изображать с помощью одной модели.
Самоорганизация и критичность
Большинство физических систем требует точной настройки внешних параметров (как температура или давление), чтобы достичь критической точки. Поэтому, критическое состояние довольно неустойчиво.
Предполагается, что существуют сложные системы с похожим поведением (бесконечный радиус корреляции, степенные функции зависимости, масштабная инвариантность и универсальное поведение, описываемое критическими индексами), которые не требуют однако настройки, и приходят в такое состояние самопроизвольно (Bak et al. 1987)[2]. Это и есть самоорганизующаяся критичность (self-organized criticality / SOC).
Состояние системы колеблется вокруг критической точки, то и дело пересекая ее, под влиянием внутренних процессов системы. Иногда говорят, что критическая точка становится «аттрактором» системы.
Кроме землетрясений и процессов образования рек, к таким системам относят лесные пожары, солнечные вспышки, нейронные лавины, стекающие по стеклу капли воды, горы и города (Marković and Gros, 2013; Fichera 2019; Andriani 2010; Golyk "Self-organized criticality").
СОК: баланс двух тенденций
Механизм генерации СОК можно свести к крайне простому объяснению. Хотя существуют разнообразные и сложные модели СОК, по существу почти все они описывают баланс двух противодействующих тенденций. Yang (2004) из бесславной Ухани показывает, как степенные распределения может дать простая модель «случайного блуждания» на «одномерной решетке»[3]. Модель СОК можно получить, кидая монетку.
Вот общее описание многих СОК-моделей в двух словах:
Взаимодействуют две противонаправленные силы[4]. Например, добавление энергии в систему и рассеивание (dissipative and driving forces). Эти силы сбалансированы так, чтобы ни одна не могла совершенно перевесить другую.
В какой-то момент они достигнут динамического равновесия. Это значит, что отклонения в ту или другую сторону возможны, но эти колебания происходит вокруг некоторого состояния, к которому система «притягивается». И отклонения и обратное движение происходит под давлением двух противодействующих сил, без всякой дополнительной настройки.
Когда это произошло, в некоторых системах возникают степенные распределения определенных свойств. В частности, размеров колебаний в динамическом балансе. Причем такое поведение не имеет характерного масштаба и случается при любых размерах системы. Это и есть критичность. Говорят, что система эволюционировала к критическому состоянию.
Можно представить себе кучу песка, в которую постепенно добавляются песчинки. Иногда случаются осыпания. Со временем возникнет более-менее крутой склон, который будет становиться то более пологим, то более крутым с добавлением новых песчинок или осыпанием. Осыпания могут быть всех размеров, и частота к размеру имеет степенное распределение. Конечно, это лишь метафора, и действующие силы (здесь — сцепление или осыпание песчинок) могут быть различными.
Итак, СОК — это:
- Открытая система — происходит обмен энергией со средой
- Взаимодействие двух тенденций
- Критическая точка — «аттрактор» системы (зона на фазовой диаграмме, к которой стремится система)
- Происходят колебания между субкритическими и сверхкритическими областями — та или другая тенденция иногда отклоняет систему от критической точки
- Степенные распределения некоторых свойств: размеров колебаний, времени между колебаниями, иногда — размеров разных участков системы. Поведение системы похоже на поведение вещества в критическом состоянии
- Масштабная инвариантность. Поведение системы описывается одними и теми же функциями на любом масштабе системы и в системах любого размера
Еще один признак самоорганизующейся критичности — дальние взаимодействия элементов в системе. И вот как они возникают.
By The Way. Пороговое поведение, лавины релаксации и связь между отдаленными элементами системы
Знаменитая абелева модель песчаной кучи (the abelian sandpile model, ASM или Bak–Tang–Wiesenfeld model, BTW) — это уже двумерная модель самоорганизующейся критичности (в отличие от одномерной модели Янга). Как видно из названия, именно для нее обычно используют метафору кучки песка с постепенно добавляющимися песчинками.
В чем особенность моделей этого типа? Чтобы получить СОК, мы задаем на микро-уровне определенные правила порогового поведения. И это важный концепт, о котором мы до сих пор не поговорили. Лавины и пороги.
Как уже было сказано, критичность — это гигантские радиусы корреляции, то-есть, зависимость поведения удаленных друг от друга частиц. «Все связано со всем». Каким образом микроскопическое поведение вызывает дальние взаимодействия? Ответ — лавины (каскады).
Каскады могут возникать в результате порогового поведения системы. Порог чувствительности — это «переключатель» между двумя режимами поведения. Допустим, участок системы испытывает на себе какое-то воздействие. Ничего не случится, пока воздействие ниже порогового. Например, на участке доски постепенно накапливаются песчинки. Накопление просто продолжается, пока склон кучки песка слишком пологий. Но когда воздействие окажется выше порогового, состояние участка может измениться резко, скачком. Песчаная горка осыплется.
В случае СОК, постепенное накопление энергии время от времени приводит к быстрым лавинам перемен. Одна из двух противодействующих тенденций (добавление энергии) подводит элементы системы к пороговому состоянию, дальше которого накопление продолжаться не может, другая (рассеивание энергии) — возвращает назад в до-пороговое состояние, как только порог будет превышен.
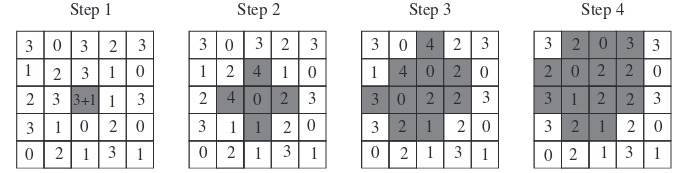
Динамика выглядит следующим образом.
1) Случайным образом (обычно с помощью равномерного распределения) выбирается один из узлов.
2) После чего добавляем к его значению h единицу, это изображает «внешний движитель» — взаимодействие системы с окружающей средой, передающей в систему энергию.
3) Если все значения h меньше 4, возвращаемся к первому шагу.
4) Если хотя бы для одного узла h больше или равно 4, узел называется «активным» или «нестабильным». Так назначен порог накопления энергии. Случайным образом выбираем любой активный узел и уменьшаем значение h этого узла на 4, а значения h каждого из соседних узлов увеличиваем на 1 — происходит «рассеивание».
5) Так как рассеивание значения h одних узлов может увеличить значение h других узлов, количество нестабильных узлов может расти после рассеивания. Повторяем предыдущий шаг, пока остался хотя бы один нестабильный узел. Когда ни одного нестабильного узла не осталось, возвращаемся к первому шагу.
Если за один шаг рассеиванию подвергаются несколько узлов, это называется лавиной. Количество участвовавших в лавине за один шаг узлов, называется размером лавины. В абелевой модели, порядок рассеивания энергии нестабильных узлов неважен.
На картинке изображено развитие лавины на квадратной решетке 5х5. Она охватывает 13 участков и длится 3 шага.
Источник иллюстрации: https://arxiv.org/pdf/0807.4838.pdf
Чтобы произошел каскад, соседние частицы (или участки) должны иметь почти-пороговое состояние, так что активация одной частицы и вызванные этим возмущения (песчинка срывается и толкает соседние) превышают порог чувствительности для других ближайших частиц, те активируются, воздействуют на следующие частицы, активируют их, и так далее. В результате, рассеивание энергии происходит на множестве участков сразу.
Похожим образом, любое малое или большое воздействие может спровоцировать экономический кризис, когда система рынка ценных бумаг эволюционировала к критическому состоянию[5].
Пороговое поведение СОК на макро-масштабе это медленное накопление и быстрые каскады рассеивания. Fichera (2019) проводит параллель с поведением земной коры, где медленным движение плит — несколько сантиметров в год — сменяется периодами быстрого высвобождения энергии в виде землетрясений, когда напряжение превышает пороговое значение, установленное трением между плитами. Причем случаются каскады всех масштабов, а их частота к размеру имеет степенное отношение.
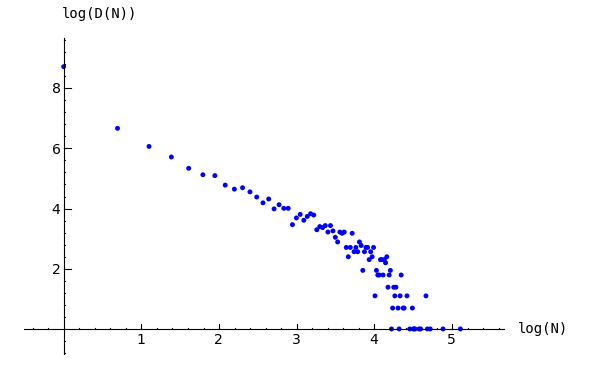
Из всего этого возникает еще одна особенность СОК-моделей: алгоритм локального порогового поведения может быть крайне простым, но дает сложное поведение системы в целом.
Пример ASM на гитхабе:
https://github.com/pmandera/sandpile-model (симуляции не проверяли).
Капитал и СОК
Как пишут Maschner and Bentley (2003), модели самоорганизующейся критичности можно применять и для социального неравенства.
Представьте, как сталкиваются и приходят в подвижный баланс две тенденции: накопление и перераспределение капитала. Производство, технический прогресс или рыночный успех приносит капиталы. Крах рынков, войны, революции и прочие потрясения провоцируют лавины перераспределения. Накопление переходит в перераспределение, когда упирается в некий пороговый уровень. Периоды медленного накопления перемежаются лавинами (сравни соображения Pianegonda et al., 2002).
Другими словами: равномерно случайный рост + случайные потрясения и катастрофы, могут задавать паттерн степенного неравенства.
Различного рода шоки — каскады подражательного поведения, войны, кризисы и даже революции — способны служить механизмом, косвенно усиливающим неравенство[6]
Действительно, ряд работ утверждает, что рынок ведет себя как система с самоорганизованной критичностью (см. в Pianegonda et al, 2002; Didier 1999; Stauffer and Sornette 1999).
Ciofc-Revilla and Midlarsky 2004 ("Power Laws, Scaling, and Fractals in The Most Lethal International and Civil Wars") показывают, что степенное распределение имеет частота/масштаб внутренних и внешних военных конфликтов.
Возможно, что и объемы накопленного в узлах или кластерах социальной сети капитала будут в таком случае описываться степенной функцией, как своеобразный «параметр порядка».

Источник — Википедия.
Очевидно, что социальные структуры вряд ли будут организованы в квадратную решетку. Некоторую информацию по СОК-эффектам на различных сетевых топологиях (в частности, на безмасштабных сетях) можно найти здесь: "Power laws and Self-Organized Criticality in Theory and Nature", Marković and Gros, 2013.
Эта статья также может послужить в качестве обзорной для моделей самоорганизующейся критичности. Вот некоторые другие статьи с широким охватом темы: "From Gaussian to Paretian Thinking: Causes and Implications of Power Laws in Organizations", Andriani and McKelvey, 2009; "Power laws, Pareto distributions and Zipf’s law", Newman, 2006; и короткая Bai-Lian Li, 2001, "Self-Organized Criticality".
Другие модели СОК
Авелева песочница[7] не дает провести прямые параллели со степенным распределением богатств. Степенное распределение здесь имеет не количество накопленной на участке энергии, а частота/размер лавин. На самом деле, о связи СОК и распределения богатства часто говорят, но с моделями все обстоит несколько хуже (пример: Chakraborty et al., 2011).
Модель, описывающая степенное распределение богатства через СОК, должна объяснять, каким образом критическое поведение системы приводит к тому, что в системе складывается большое число участков с небольшим «размером» (или количеством энергии), незначительное число средних участков, и единицы крупных.
Можно представить, как ряд «предпринимателей» постепенно накапливает богатства, растущие с равномерной случайностью. Но иногда проходят лавины. Лавины в масштабе всей системы, которые уравнивали бы всех, хотя и случаются, но редко. Чаще всего, лавины подолгу оставляют в покое некоторых отдельных предпринимателей, дают шансы накопить сколько-то богатства небольшому числу, и периодически накрывают с головой большинство. Или же лавины определенным образом перераспределяют богатства участников. Впрочем, не факт, что это получится показать на модели.
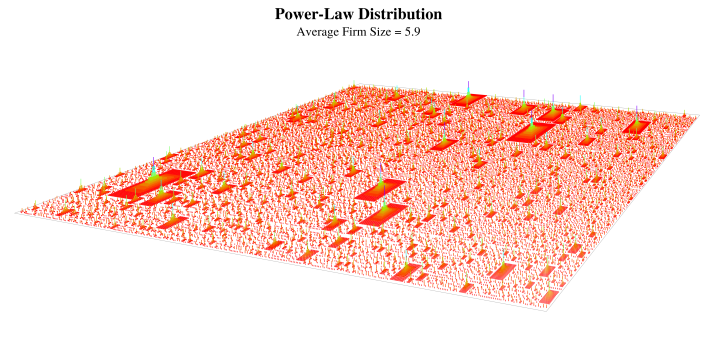
Пара других моделей, которые цепляют внимание[8]:
1) Лесной пожар (Critical Forest Fire / Forest-fire model)
Опять клеточные автоматы на двумерной решетке (Grassberger 1993; ссылается на Drossel and Schwabl 1992).
Есть три типа клеток: 1) «зеленые деревья» могут независимо от соседних загореться с некоторой вероятностью q, 2) «горящие деревья» переходят в 3) «выжженную землю» и поджигают соседние «зеленые деревья» в течение одного шага. С вероятностью p, на «выжженной земле» вырастают новые «деревья». Детали могут отличаться в разных вариантах модели.
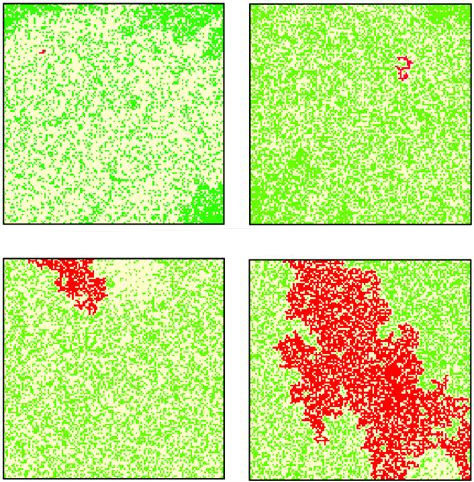
Таким образом, в модели взаимодействуют две тенденции: «пожары», которые способны охватывать сообщающиеся кластеры «деревьев», и «естественный рост» «деревьев». При определенных условиях, распределение размеров кластеров будет напоминать степенное (в Grassberger 1993 приводится график с усеченным концом хвоста, как это часто бывает и в распределении богатства).
Модель на гитхабе: https://github.com/y-taka-23/elm-forestfire
Этот тип моделей может показаться лучшей метафорой для постепенного накопления и периодического перераспределения капитала — по крайней мере, на первый взгляд.
2) «Игра в жизнь» (ИЖ)
Пожалуй, самая интересная из моделей, так или иначе связывающих критичность и распределение богатства, описана у Del Faro-Odi et al., в работе 2019 года "Thermal and Superthermal Income Classes in a Wealth Alike Distribution Generated by Conway’s Game of Life Cellular Automaton". Кажется, ИЖ не является СОК в классическом виде - она проходит стадию критичности и в итоге приходит к «станционарному состоянию». Но версия ИЖ, приведенная Баком в его популярной книге, где периодически добавляются новые клетки - и эти внешние возмущения вызываюь лавины - может добавить в ИЖ элемент самоорганизации в сторону критичности.
Это едва ли не единственная работа из найденных, которая обещает степенной хвост и показывает степенной хвост в верхнем экономическом классе, причем обрезанный в конце, как это бывает и с реальным богатством. Нижний экономический класс следует экспоненциальным распределениям.
Экономическим агентом здесь считается клетка решетки, а богатство определяется количеством «возрождений» клетки.
Противодействующие силы
И хотя мы нашли немного сколько-нибудь интересных работ[9], где концепт СОК используется, чтобы объяснить степенное неравенство богатства, можно вообразить себе, как существующие модели СОК могли бы послужить метафорами накопления капитала, и какие действующие в социальных системах силы можно было бы сопоставить с двумя противодействующими тенденциями модели.
Очевидно, без сопутствующей большой работы, это только фантазии:
- Взаимодействуют положительный и отрицательный эффект масштаба. Большие системы имеют свои плюсы и свои минусы. Крупное производство может быть дешевле, крупная политическая система — влиятельнее. Но также большие системы могут быть неповоротливыми или хрупкими. Существует динамический баланс положительных и отрицательных эффектов масштаба, и этот баланс приводит к степенному распределению размеров организаций
- Можно представить и взаимодействие других двух сил. Стремление организаций к экспансии и потолок сложности, выше которого управление становится затруднительным. В каком-то смысле, это то же самое, но другими словами. Организации стремятся захватывать все больше территорий и ресурсов, но в определенный момент сталкиваются с пороговой сложностью управления. Превышая порог, организации теряют управление. Этот порог может меняться с развитием средств управления
- Еще одна пара. Рост экономики и кризисы
- Социальное напряжение из-за неравенства и социальные взрывы
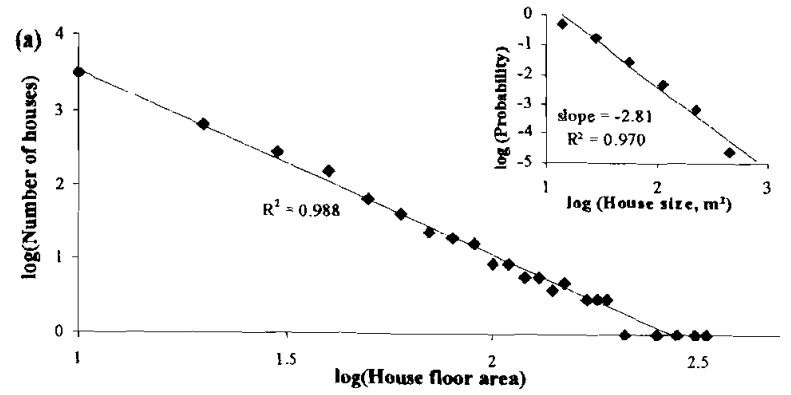
Maschner and Bentley предполагают, что степенное распределение статуса и ресурсов на индивидуальном уровне может быть результатом конкуренции. В каждом обществе есть индивиды, которые конкурируют за доступ к ресурсам и репродуктивным партнерам. Благодаря этому складывается «рынок престижа», на котором лидеры конкурируют за последователей, которые в свою очередь желают превзойти, а если это невозможно, то быть связанными с успешными лидерами. Процессы на этом рынке можно моделировать так же, как на рынке инвесторов с Уолл-Стрит.
Можем ли мы сказать, что в системе таким образом взаимодействуют «приспособленность» и «давление отбора»?
В этом забавном видео, предлагают совместить лозунг "eat the rich" и анархо-капитализм. Дайте богатым свободно расти, а потом периодически их съедайте. Возможно, эта шутка хорошо иллюстрирует планы запретительной борьбы с богатыми, которые лелеют некоторые социалисты. Вместо того, чтобы одним шагом достичь цели, как это представляется в механистическом видении общества, социалист ввязывается в длительную борьбу. На самом деле он создает процесс, в котором взаимодействуют две противонаправленные тенденции: стремление социалиста прижать богача, и стремление богача сохранить капиталы. Давление социалиста уменьшит богатства большинства неудачников из числа богачей, и даст преимущество меньшинству счастливчиков. Причем проще окажется прижать людей, у которых богатства меньше. Процесс такого рода способен формировать степенное неравенство богатства, а вовсе не разрушать его. По крайней мере, пока баланс между силами не нарушится, и регулирующие институты не будут способны полностью контролировать и подавлять неучтенную низовую активность. Но в этот момент, они станут самым крупным капиталистом в игре.
Впрочем, этот пример больше напоминает не СОК, а ВОТ.
СОК и ВОТ
Несколько похожая на СОК концепция — «высоко оптимизированная толерантность» (highly optimized tolerance, HOT).
Телеграф обрезал часть текста, вот окончание:
https://telegra.ph/critical-power-09-30
Канал: @AnarchyPlus.
_______________
[1] Чтобы узнать больше, читайте о гипотезе универсальности и методе ренормгруппы.
[2] Несмотря на то что стартовая работа Бака и компании была несколько претенциозна, а популярные трактовки кажутся слишком восторженными, концепция прижилась, и ряд разработанных в ее рамках моделей периодически используется различными исследователями. Конечно, СОК не «объясняет природу сложности», как утверждали желтые заголовки, и вовсе не является главным способом объяснять степенные паттерны в различных процессах, однако она кажется достаточно интересной, чтобы упомянуть в текущей серии.
[3] Представьте цепочку из узлов, по которой случайным образом движется фишка. Для движения в ту или другую сторону могут назначаться разные вероятности. В модели Янга, степенное распределение размеров «колебаний» (количество шагов от одного пересечения фишкой стартового узла до следующего пересечения) возникает, когда эти вероятности сбалансированы примерно по 0.5.
[4] Кажется, вся суть таких моделей в том, что две величины с распределениями экспоненциального класса, могут при взаимодействии каким-то образом давать степенные распределения. Поправьте, если это бессмыслица.
[5] В неакадемической заметке "Cause-and-Effect or Fooled by Randomness?" проводится параллель с “food network” СОК-моделью за авторством Amaral-Meyer — это модель пищевой сети, в которой случайное вымирание одного вида имеет степенное отношение к разрушительности последствий для сети в целом (также см. Andriani and McKelvey, 2009). Автор указывает на сходство с моделями краха финансового рынка в 2008.
[6] Хотя есть тонкости: по графикам Пикетти видно, что мировые войны скорее снизили мировое неравенство. Впрочем, это может быть связано с масштабом каскада — лавина охватила значительную часть системы.
Кроме того. Революция может снизить внутреннее неравенство в стране, но увеличить неравенство между странами, или же увеличить неравенство не подрывая, а усиливая экономический потенциал страны, как революции в Америке и Европе. Т.е, сами по себе шоки здесь могут не только уменьшать «количество энергии на участке», но и увеличивать.
И наконец, разные эффекты могут проявляться на разных временных горизонтах — революция могла бы разорить страну в короткой перспективе, но дать подъем в долгосрочной (Франция, Америка, Англия).
[7] Даже абелева группа превращается в притчу, когда математик рождается в семье протестанта. Сыпется ли песок из Каина? Как представить себе каиновы группы?
[8] Еще один класс моделей — модели со случайным барьером. Здесь заимодействуют такие две тенедции: есть некоторое количество объектов (часто изображают как палочки с определенной высотой), которым с равномерной случайностью задается размер от 0 до 1. Есть «катастрофы», которые периодически срезают все объекты ниже случайно определенного размера, и снова заменяют их объектами с равномерно распределенными случайными размерами. Распределение размеров лавин окажется степенным. Детали моделей могут отличаться.
В приложении к распределению богатства, похожий принцип использует работа "Conservative self-organized extremal model for wealth distribution" by Chakraborty et al., 2011.
[9] Несколько моделей претендуют на то, чтобы симулировать неравное распределение богатства в обществе, и даже подчеркивают, что паттерн неравенства должен иметь степенной хвост, но затем... предлагают нам гауссиану или другие распределения экспоненциального класса (Pianegonda 2002; Chakraborty et al., 2011). Дугие обещают продемонстрировать СОК, и... описывают кумулятивное накопление (Levy and Solomon).
Pianegonda и друзья в одном месте говорят про распределение с «линейным поведением», а в другом называют его же степенным. При этом они не упоминают каких-либо тестов.
Пишут, что нечто интересное может быть здесь — "Scaling behaviour in the growth of companies" by Stanley et al., 1996 — но нам не хватило времени прочесть.
Весьма любопытная — и популярно написанная — статья, которая использует концепт СОК, чтобы объяснить социальные явления — это Revilla and Midlarsky, "Power Laws, Scaling, and Fractals in The Most Lethal International and Civil Wars".