Тяжелые хвосты и нормальное равенство. Часть 1

Давайте попробуем представить, как можно говорить об иерархическом и эгалитарном обществе с точки зрения формы распределения вероятностей для некоторых свойств популяции.

Текст можно разбить на несколько смысловых блоков.

1) Сначала мы расскажем о том, как выглядит паттерн для неравенства в росте, физической силе и интеллекте.

2) Потом — какой паттерн наблюдается в распределении богатства, что в нем особенного, и какие механизмы могут его вызывать.

3) В третьем блоке речь пойдет о том, как люди представляют себе равенство, и как его представлять не нужно.

4) И наконец, мы сделаем предположение, как выглядит действительное социальное равенство, судя по археологическим данным — вывод неожиданный, парадоксальный, и открывающий новые перспективы для обсуждения проблемы. Равенство, как вы его представляли — это не совсем равенство, а реальное равенство может оказаться непохожим на ваши мечты. И это хорошо!

Этот текст — вводный. Наша цель — заинтересовать вас в обсуждении проблемы, предложить современные инструменты и стартовые отсылки к источникам. Мы ожидаем опровержения и дополнения — через бота @AnarchyGoBot можно договориться о публикации. Пожалуйста, поправьте наши ошибки, если вы лучше разбираетесь в вопросе.

Введение, которое можно пропустить

Описывать большие системы: распределение вероятностей

Из-за недостатка данных или чрезмерной сложности вычислений, мы не всегда можем описать какую-либо систему подробно и детерминированно. Поэтому, есть способы описывать свойства больших систем, не вдаваясь в детали. Один из них — показать, как то или другое отдельное свойство распределено по элементам системы. Например, сколько людей в популяции обладает какой частью богатства.

На практике это обычно означает, что нужно собрать часть данных о том как распределено это свойство, и сделать предположение о закономерности распределения, которая действует в системе. Чтобы обобщить реальные данные, используются математические модели, которые называются «распределениями вероятностей». Реальные данные не соответствуют модели распределения идеально, а только с той или другой степенью точности.

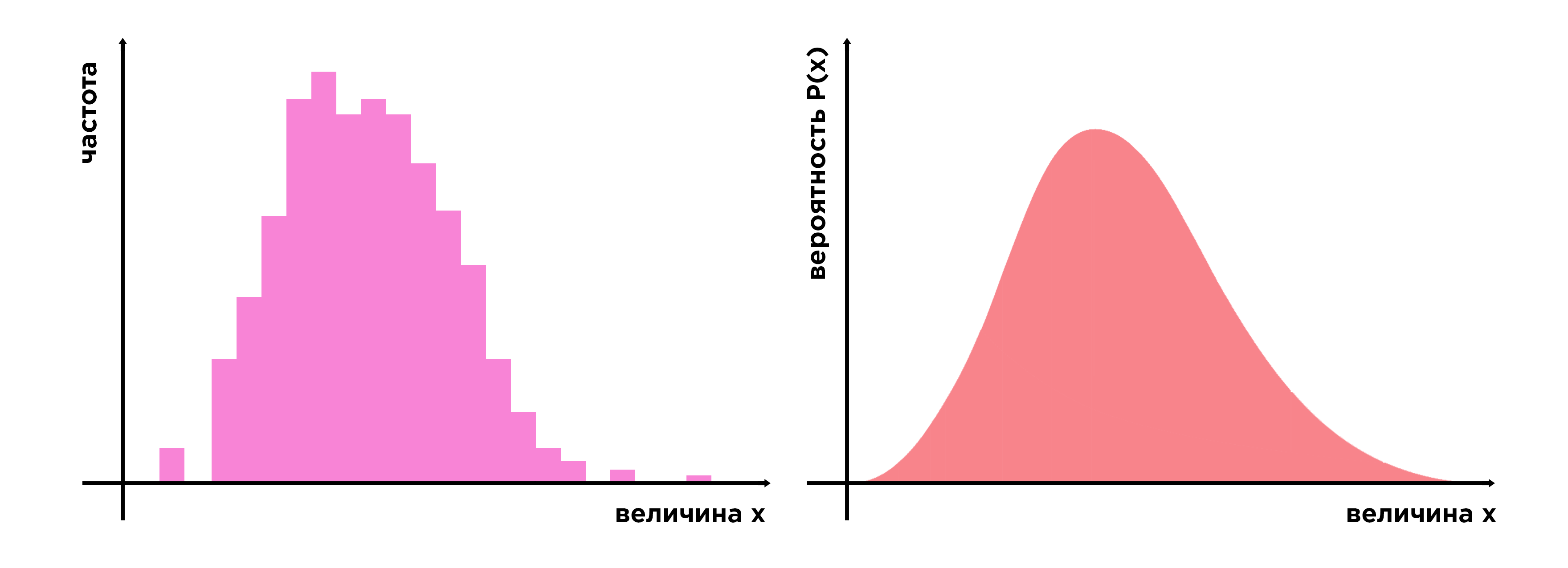
Существует множество моделей распределения вероятностей, но мы обсудим только несколько из них — те, которые могут оказаться интересны при обсуждении проблемы неравенства в обществе.

Несколько распределений

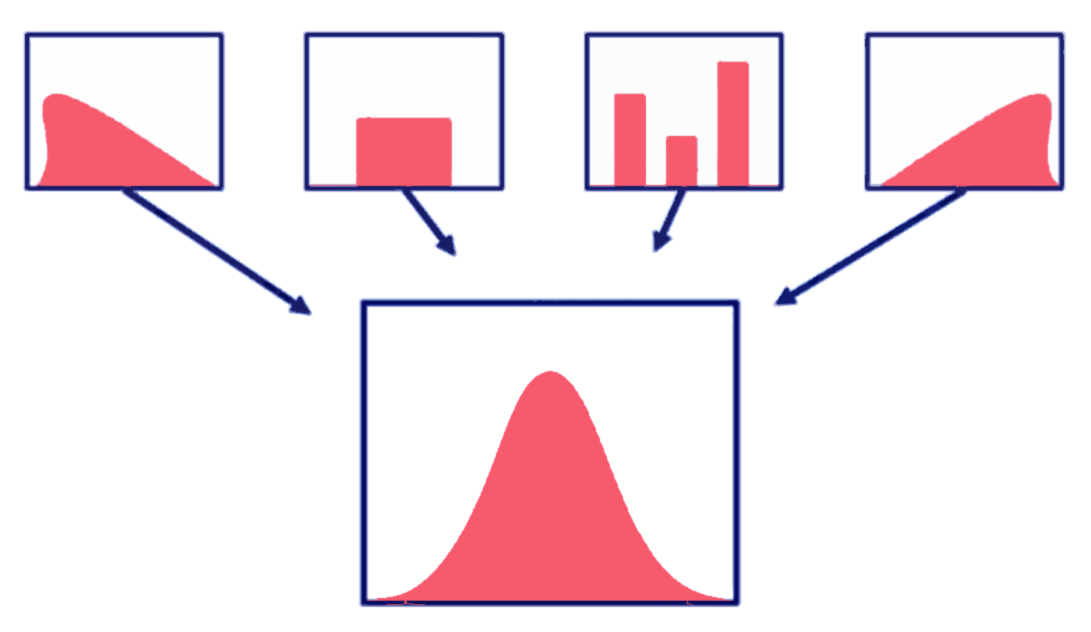
Распределения различных свойств или отличающегося масштаба могут иметь нечто общее: схожую форму. На картинке ниже изображены графики трех моделей распределения вероятностей, которые широко используются на практике, потому что распределение реальных данных часто имеет похожий паттерн. Это модели нормального, степенного и прямоугольного распределения вероятностей. 

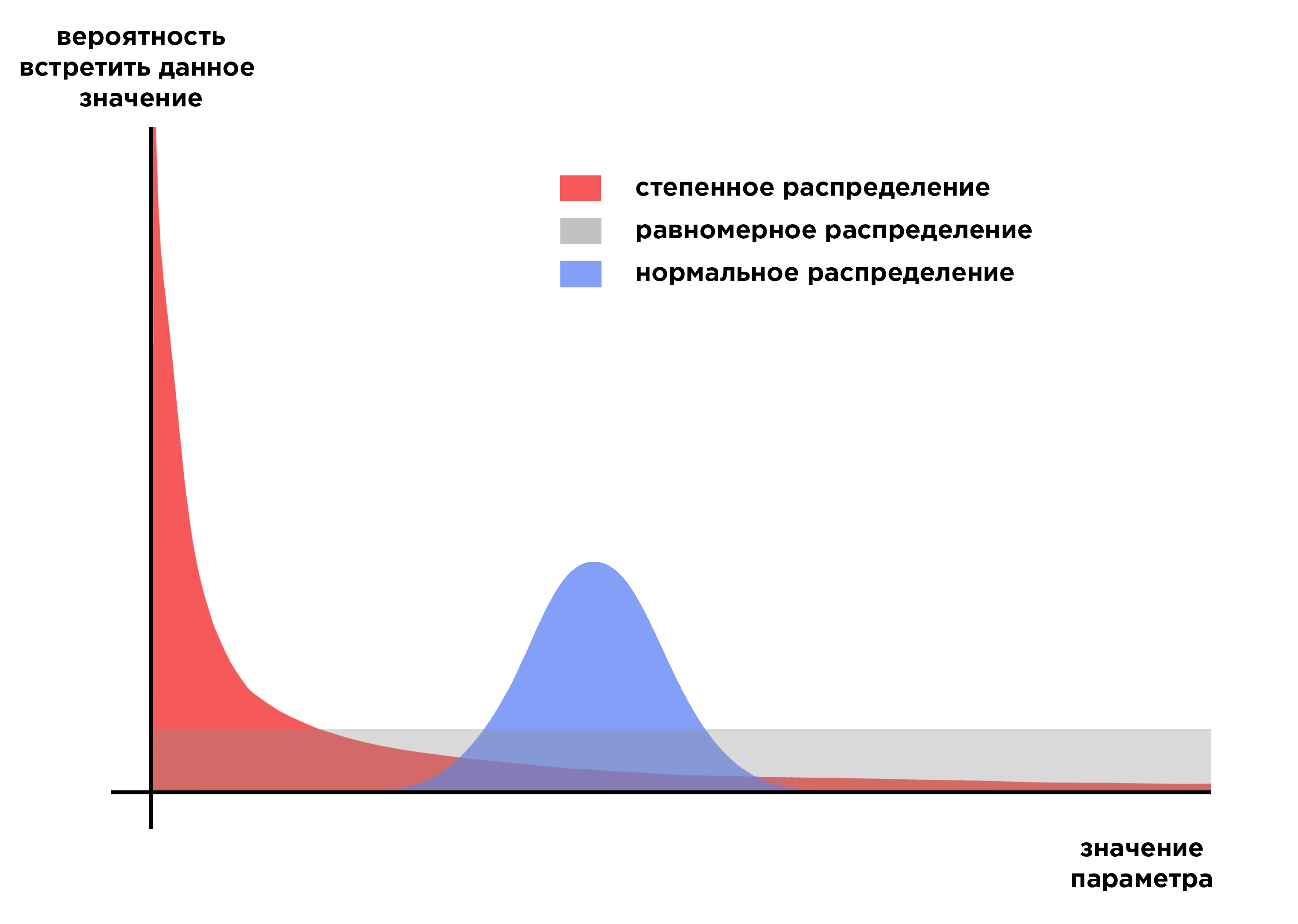
График PDF нормального распределения имеет колоколообразную форму. Если взять из популяции случайного человека, с наибольшей вероятностью он будет иметь среднее значение параметра, который мы моделируем. Другими словами, людей со средним значением больше всего. Большая часть популяции будет относительно слабо отклоняться от среднего значения параметра. И наконец, немногочисленные крайние значения относительно недалеко уходят от основной группы — «хвосты» распределения быстро затухают.

График PDF равномерного распределения выглядит как прямоугольник. Это значит, что случайно взятый из популяции человек будет с одинаковой вероятностью иметь любое значение параметра в диапазоне распределения. Модель подойдет, если людей с каждым значением параметра одинаковое количество.

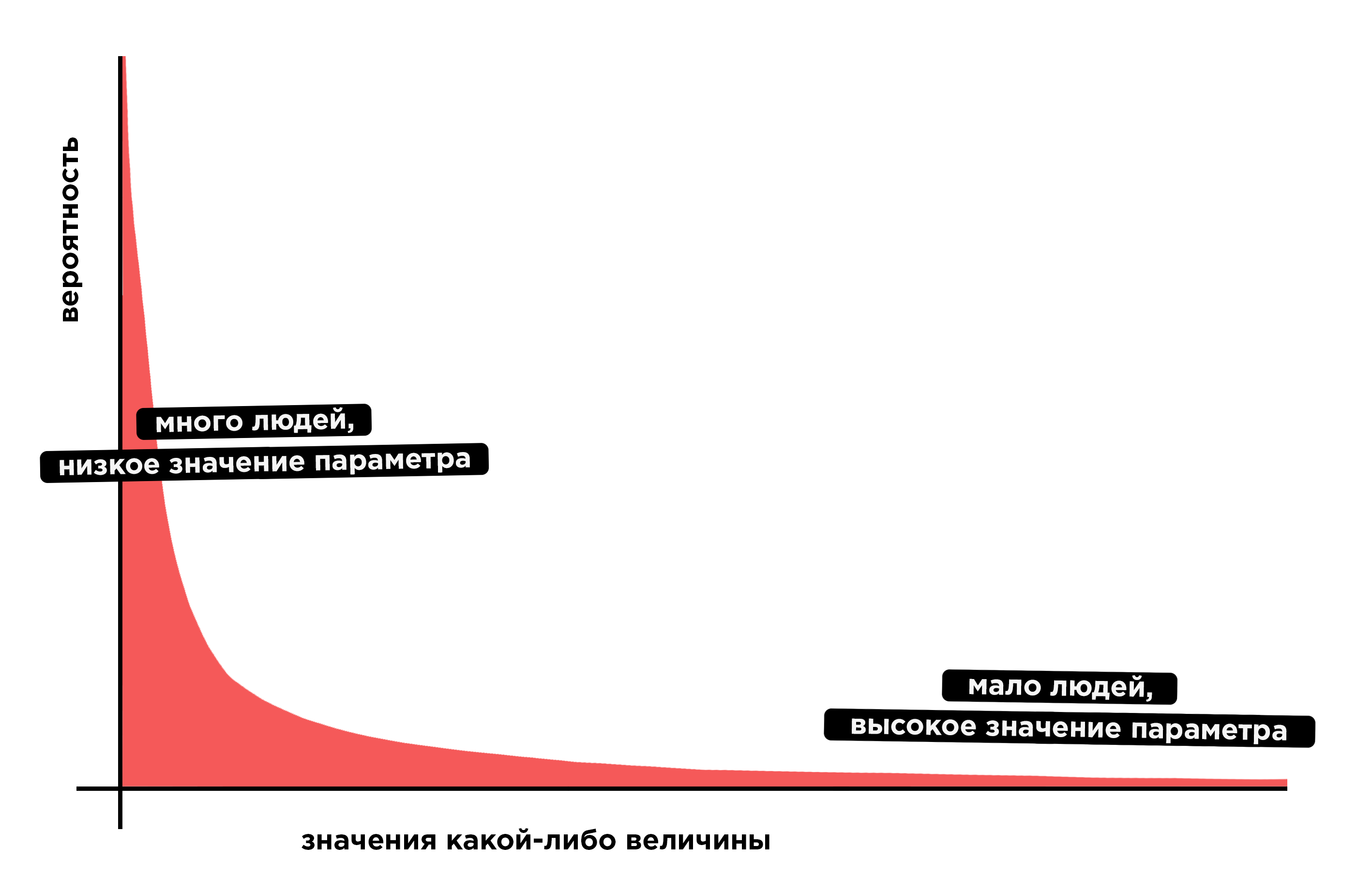
График PDF степенного распределения — гипербола. Случайно взятый представитель популяции с наибольшей вероятностью будет иметь низкое значение параметра. Лишь с очень небольшими, хотя все же реальными, шансами, значение исследуемого параметра окажется у выбранного человека высоким. 

Итак, рассмотрим различные общественные структуры с точки зрения паттернов распределения.

Блок 1

Нормально ли неравенство?

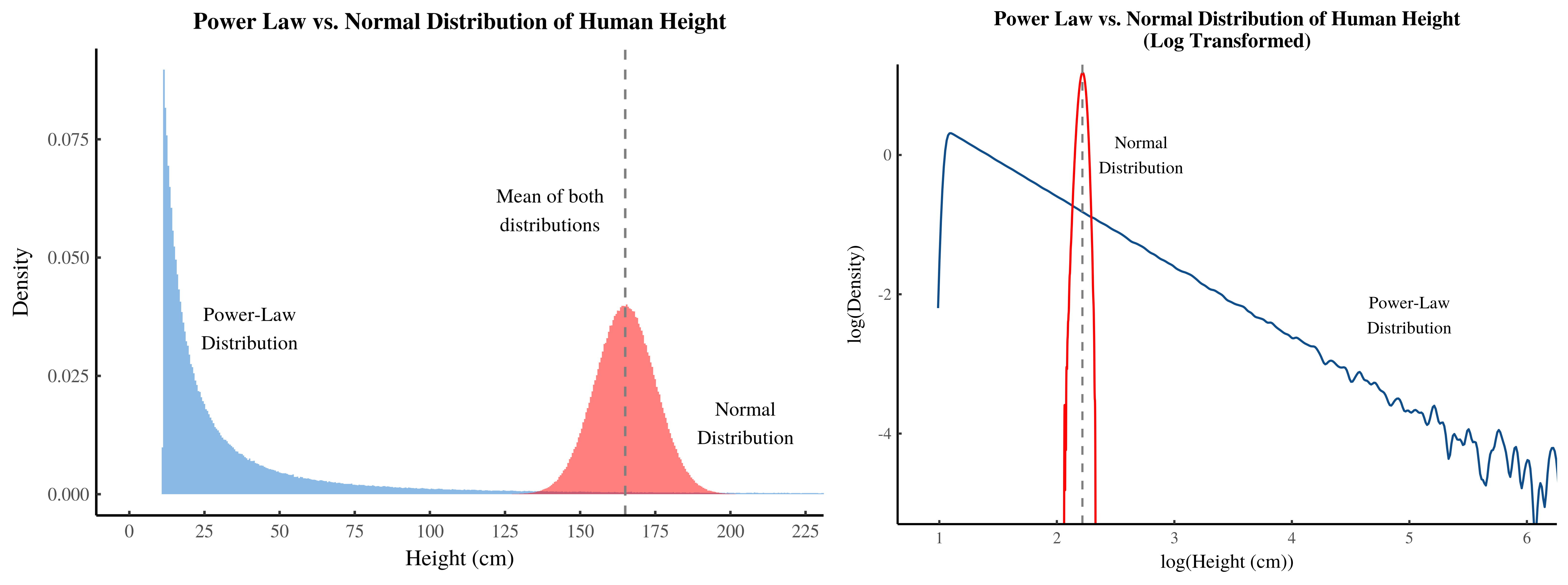
Традиционный аргумент сторонников социального неравенства: «люди не равны от природы»*. Это действительно так. Люди различны по свойствам. И многие из этих свойств подчиняются нормальному распределению. К примеру, измерения роста, физической силы или интеллекта** нормально распределены по популяции. Вот как выглядят графики распределения роста и силы хвата:

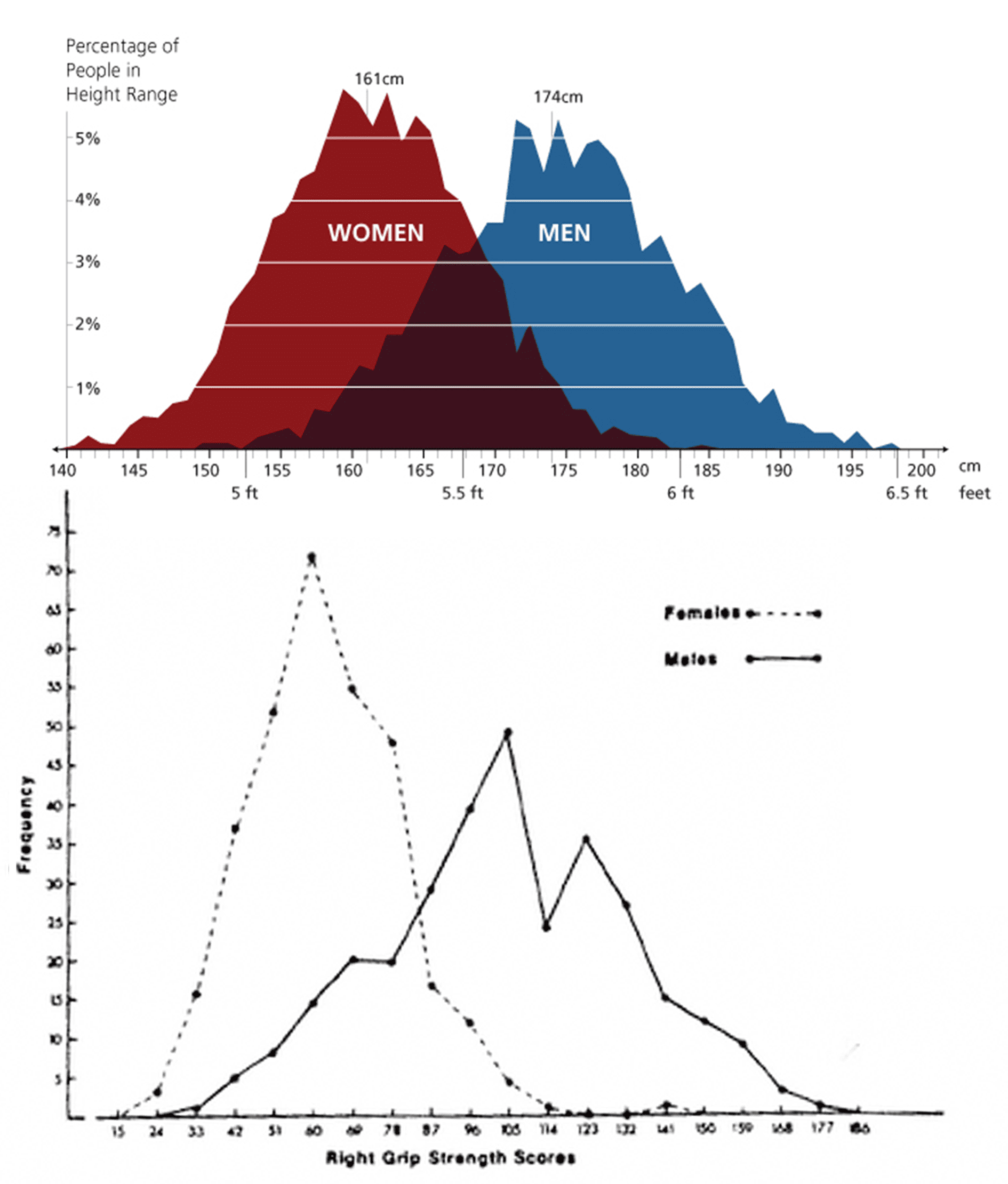
Мораль аргумента могла бы звучать подобным образом: «существует естественное неравенство, которое мы обнаруживаем повсюду, и социальное неравенство — это лишь еще одно явление в ряду других похожих явлений. Вещь того же характера, что неравенство роста или интеллекта». Услышав это рассуждение, можно подумать, что социальное неравенство выглядит примерно так:

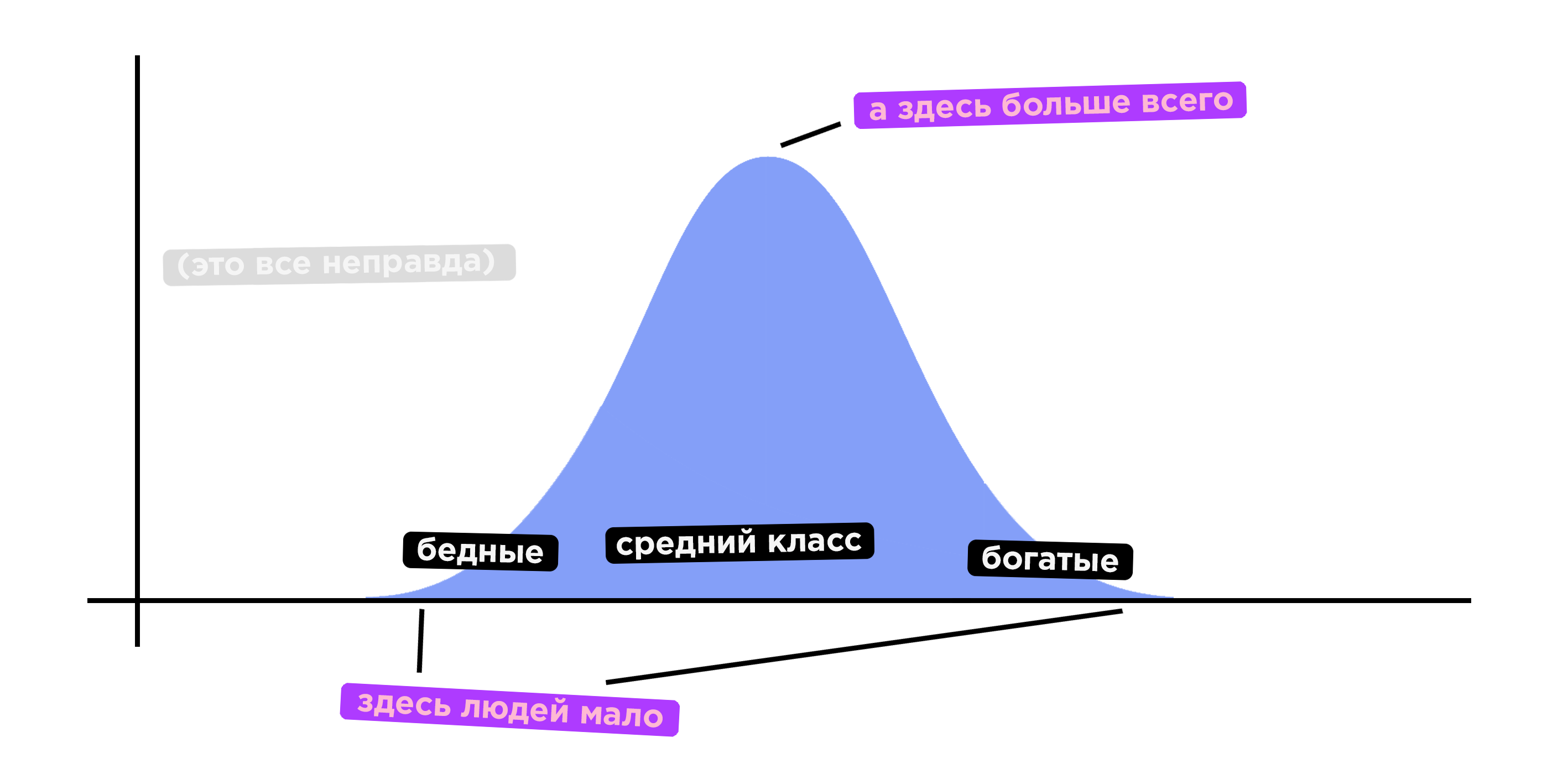
Но распределение богатства и власти не подчиняется нормальному закону. Богатство и власть имеют степенное распределение.

Механизм нормального распределения

Какие процессы стоят за нормальным распределением?

Можно грубо сказать, что нормальное распределение складывается, когда какую-либо случайную величину определяет достаточно много независимых друг от друга случайных факторов, каждый из которых влияет на результат незначительно (центральные предельные теоремы; ЦПТ Ляпунова).

Нормальное распределение роста скорее всего означает, что нет никакой крупномасштабной закономерности, которая бы влияла на рост людей. Вместо этого, рост определяется большим количеством независимых причин. Иначе дело обстоит с распределением статуса и благ в обществе.

Блок 2

Вездесущий степенной закон

Характерная черта сетей с фрактальным или безмасштабным ростом — степенные распределения свойств. Степенные распределения встречаются повсюду в социальных системах. Примеры: известность сайтов в Интернете, граф знакомств голливудских актеров, интенсивность военных конфликтов (Sun 2004; Cioffi-Revilla and Midlarsky 2013).

Maschner and Bentley (2003) упоминают примеры степенного распределения статуса по данным антропологии: степенным законом описываются размер жилищ на Алеутских островах, размеры деревень в Полинезии, участие воинов племени Yanomamo в убийствах. Как показывает Bodley (1999), степенное распределение имеют размеры социальных систем (по количеству участников) на различных уровнях и в различных сферах: сети обмена, комерческие предприятия, политии.

Вильфредо Парето (Pareto 1906, 1927) открыл степенные распределения в экономике — и частный случай степенного распределения назван по его имени. Выяснилось, что степенному закону (как минимум для верхнего класса богатых) следует распределение доходов и благосостояния в национальных экономиках.

После Парето, гипотеза о степенном распределении ресурсов была многократно проверена на других данных.

Abul-Magd (2002) предполагает степенное распределение богатства в древнем Египте в период царствования Эхнатона (14 век до Р.Х.) на основе данных о площади жилищ. Hegyi et al. (2005) обнаружили степенное распределение богатства для семей аристократов в средневековой Венгрии (парето-индекс 0.92). Klass et al. (2006) показывают, что богатство четырехсот богатейших людей из списка Forbes имеет распределение по Парето со средней степенью 1.49 (но Chan et al. 2017 предлагают другое распределение для этих данных). Okuyama et al. (1999) описывают степенное распределение доходов японских фирм (со степенью 1). Axtell (2001) — степенное распределение выручки, рыночной капитализации и размеров по количеству работников для американских фирм. Levy and Solomon (1997), а также Dragulescu and Yakovenko (2001) обнаруживают степенной закон в хвосте распределения доходов в США. Sinha 2006 находит степенное распределение богатства в Индии. Bodley (1999) показывает, что неравенство благосостояния, следующее степенному закону, присутствует на самых разных масштабах в современном обществе, от далеких деревень до крупных городов, и в самых различных системах, включая политии, сети обмена или стоимость жилищ.

Не пирамида

Что такого особенного в степенном распределении?

Во-первых, для степенного распределения характерна масштабная инвариантность. Это значит, что какой бы масштаб системы мы не рассматривали, пропорция между значениями вероятности и обсуждаемой величины будет той же самой. Именно поэтому, на двойных логарифмических координатах, степенное распределение выглядит, как прямая линия. Это и некоторые другие свойства степенного распределения позволяют сделать интересные предположения о закономерностях, которые стоят за его возникновением. 

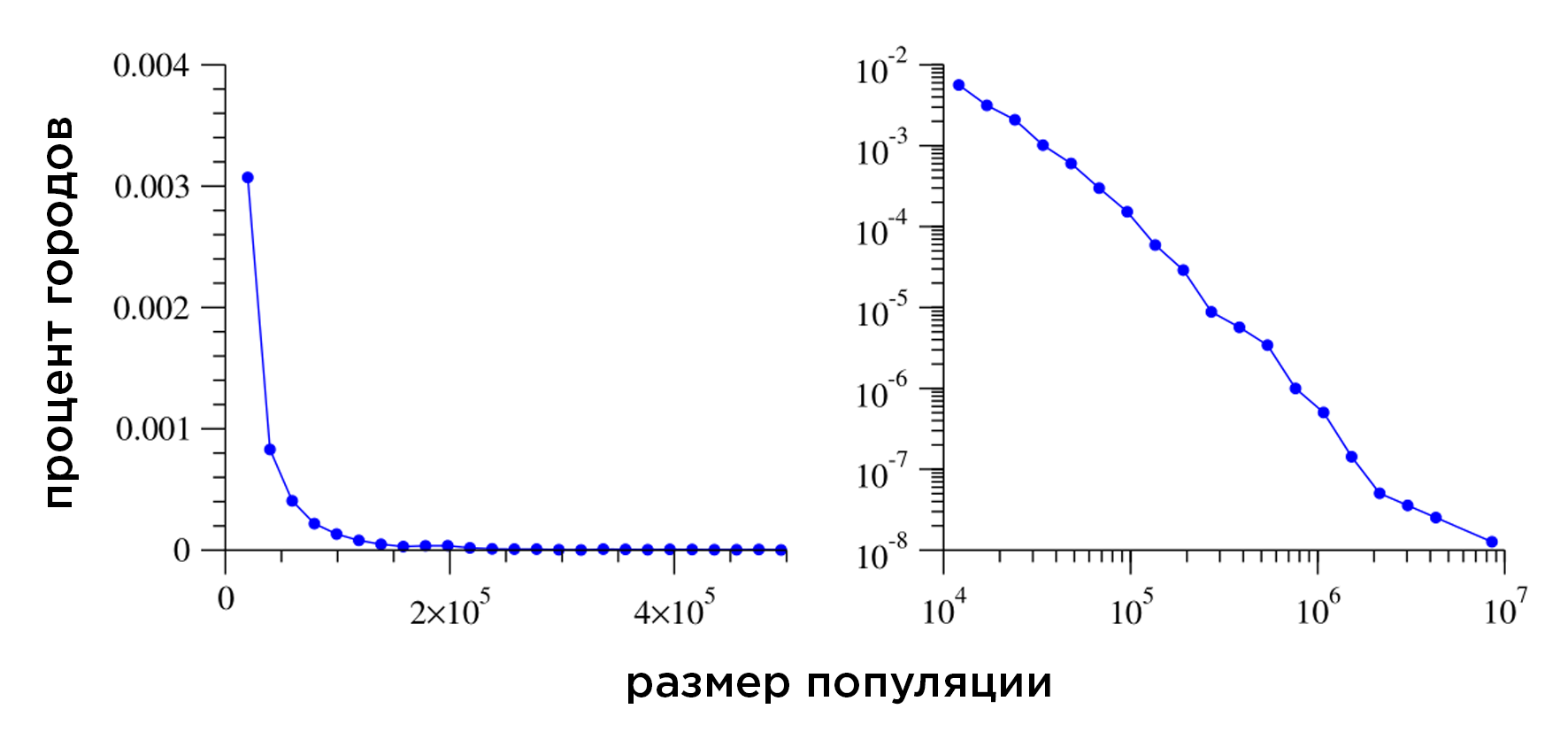
Во-вторых, его необычная форма. Не просто есть бедные и богатые: различия между ними крайне сильно выражены и совсем непохожи на паттерн нормального распределения. Большая часть популяции «находится» в левой части распределения, и в совокупности обладает меньшей частью богатства. Незначительная доля популяции располагается в середине. В узкой части графика справа находится малое число сверхбогатых, которые обладают большей частью ресурсов. Разница между большинством и сверхбогатыми простирается на много порядков величины.

Интуитивное представление о социальном неравенстве рисует образы, как будто из памфлетов времен Великой Французской революции: пирамида, и на каждом следующем этаже стоит слегка меньшая группа, которая однако обладает слегка большей долей богатства. На модели распределения мы ожидали бы увидеть нечто вроде склона привычной колоколообразной кривой. Но этот интуитивный образ дает ошибочное представление об истинных пропорциях неравенства.

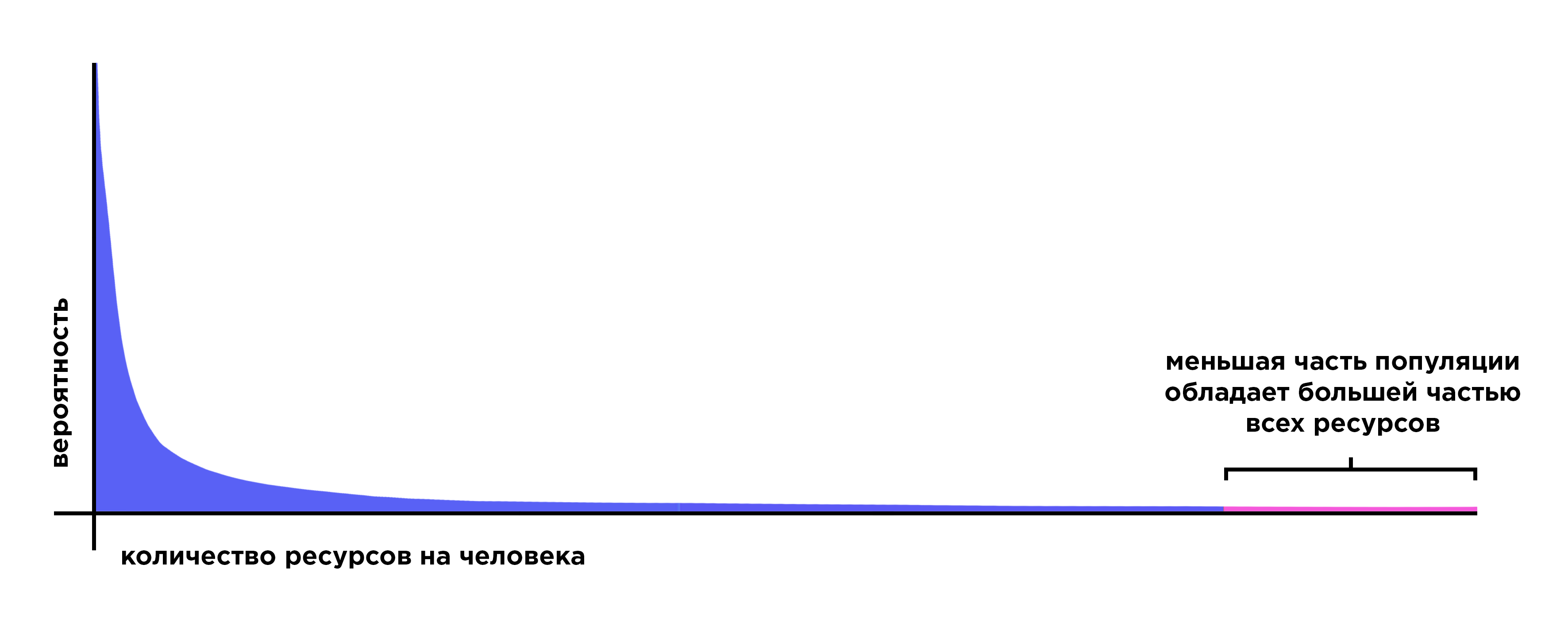
Когда разговор заходит о паттерне степенного распределения, вы можете услышать забавную фразу: «тяжелый хвост». Именно «тяжелый хвост» — отличительная особенность социального неравенства на реальных данных. Что это такое?

Неравенство с тяжелым хвостом

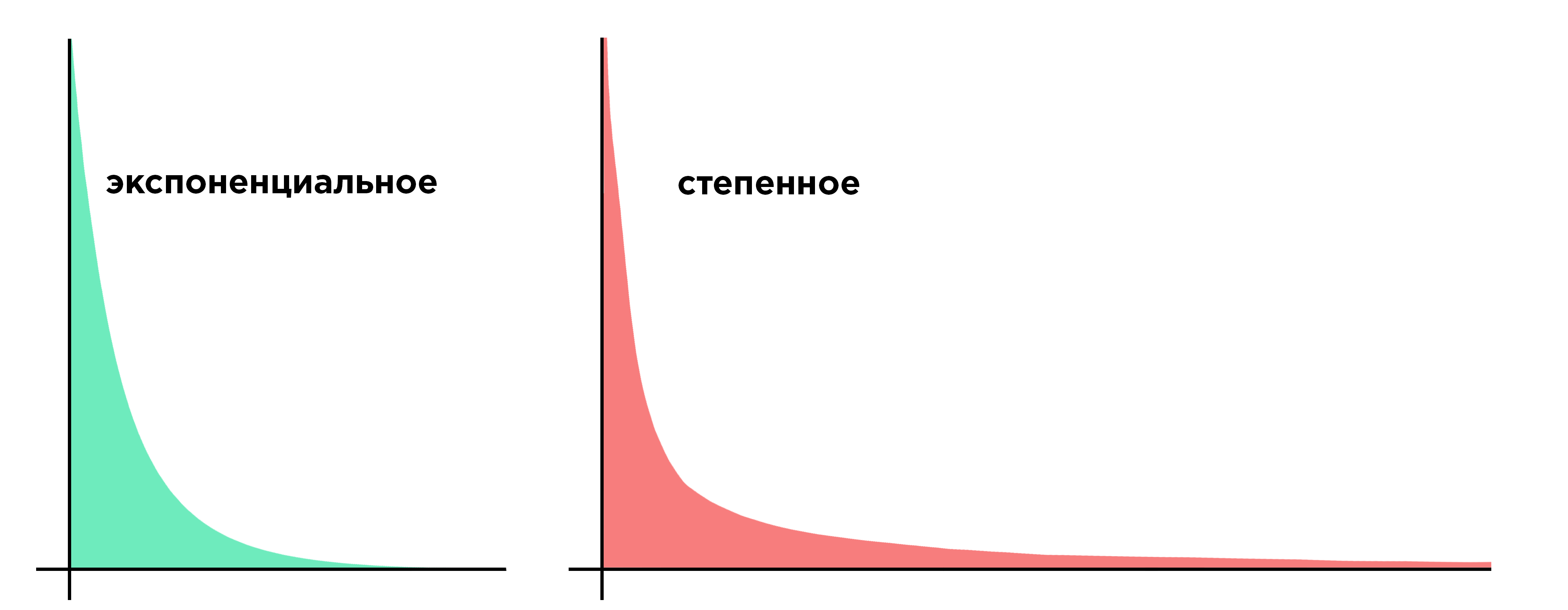
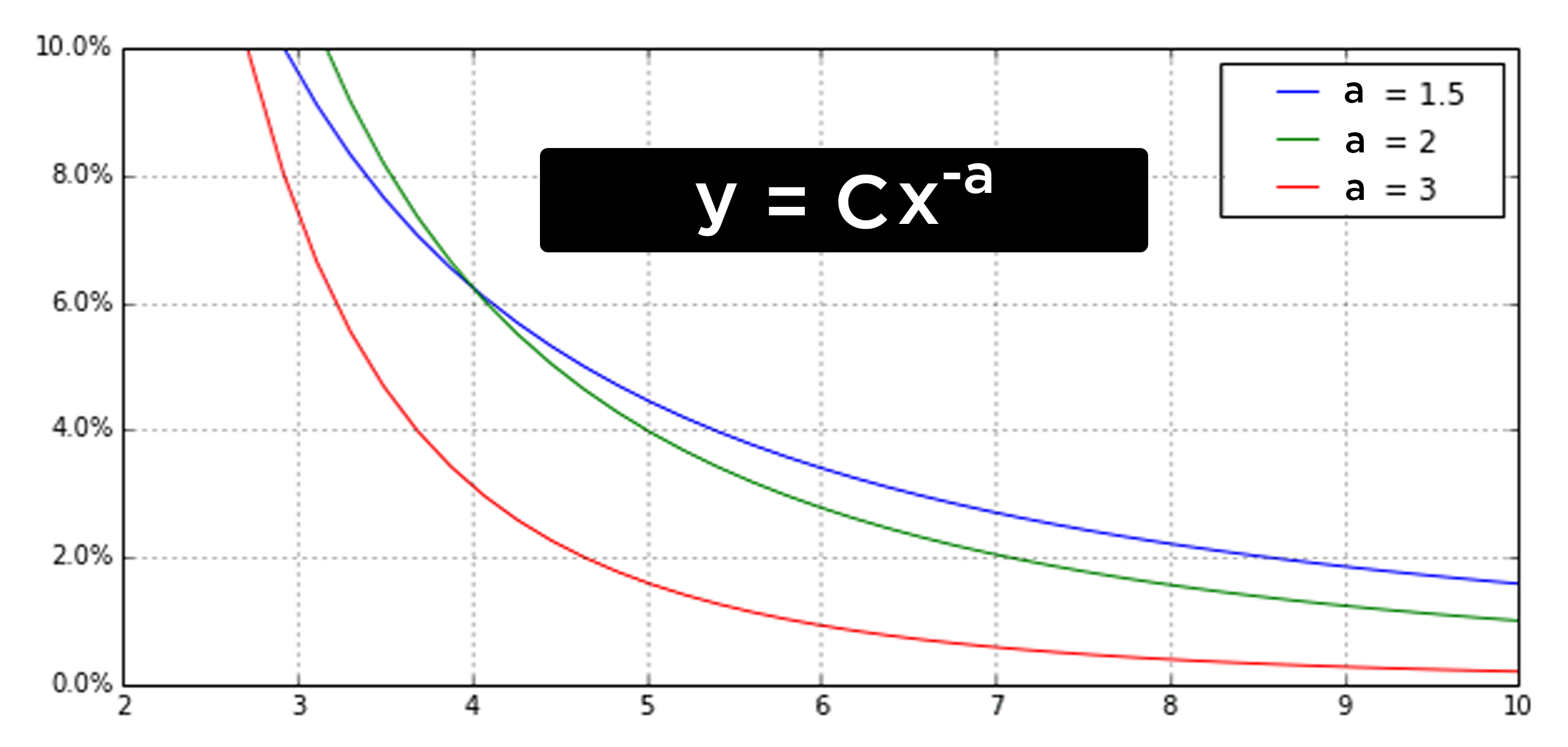
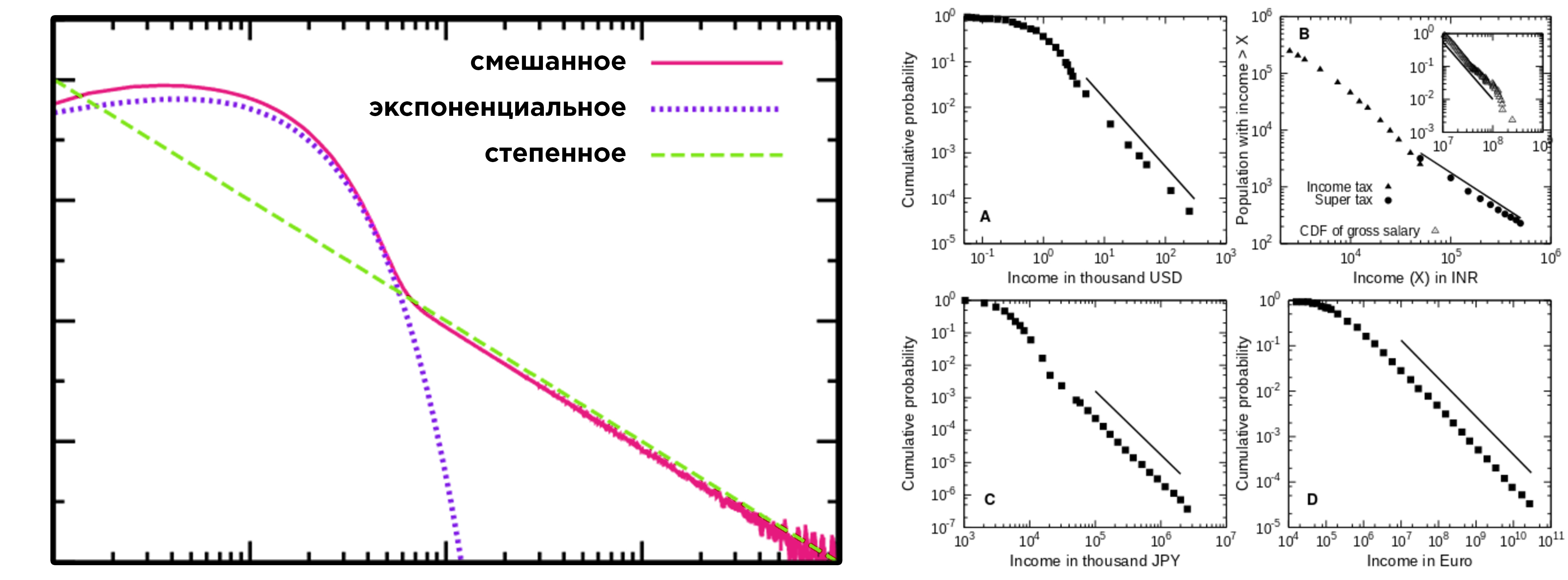
График степенного распределения на первый взгляд может показаться похожим на график экспоненциального распределения. Ключевая разница в том что функция степенного распределения (с определенными параметрами) убывает медленнее, чем функция экспоненциального. На графике степенное распределение имеет вытянутую у основания правую часть (правый «хвост» распределения).

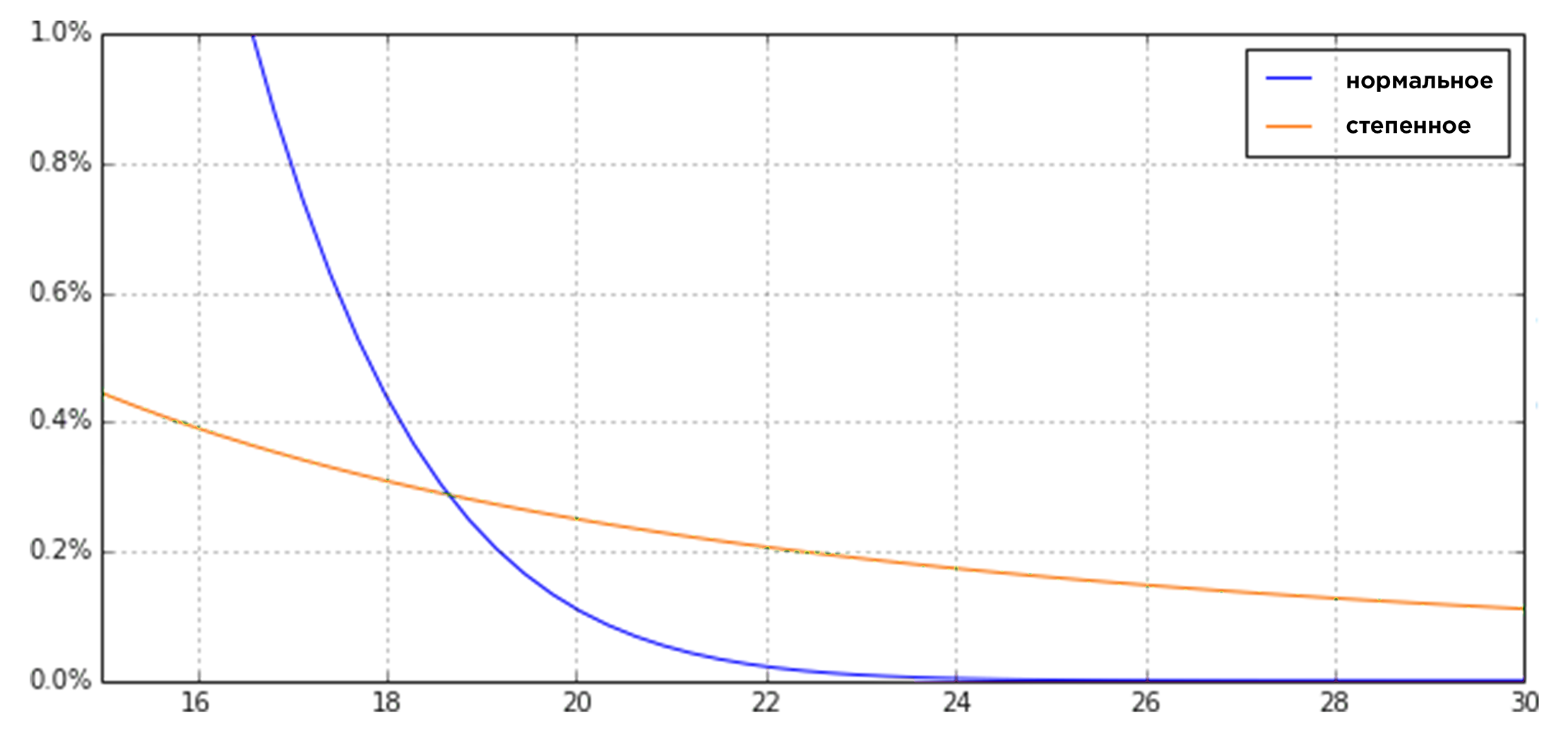
Хотя определения могут отличаться от места к месту, убывающий медленнее экспоненты хвосты распределения, иногда называются субэкспоненциальными или «тяжелыми». «Тяжелые хвосты» противопоставляются «тонким», которые убывают экспоненциально или быстрее экспоненты. Надо отметить, что существуют вероятностные распределения, у которых «тяжелый хвост» убывает быстрее, чем у степенного, но медленнее, чем у экспоненциального.

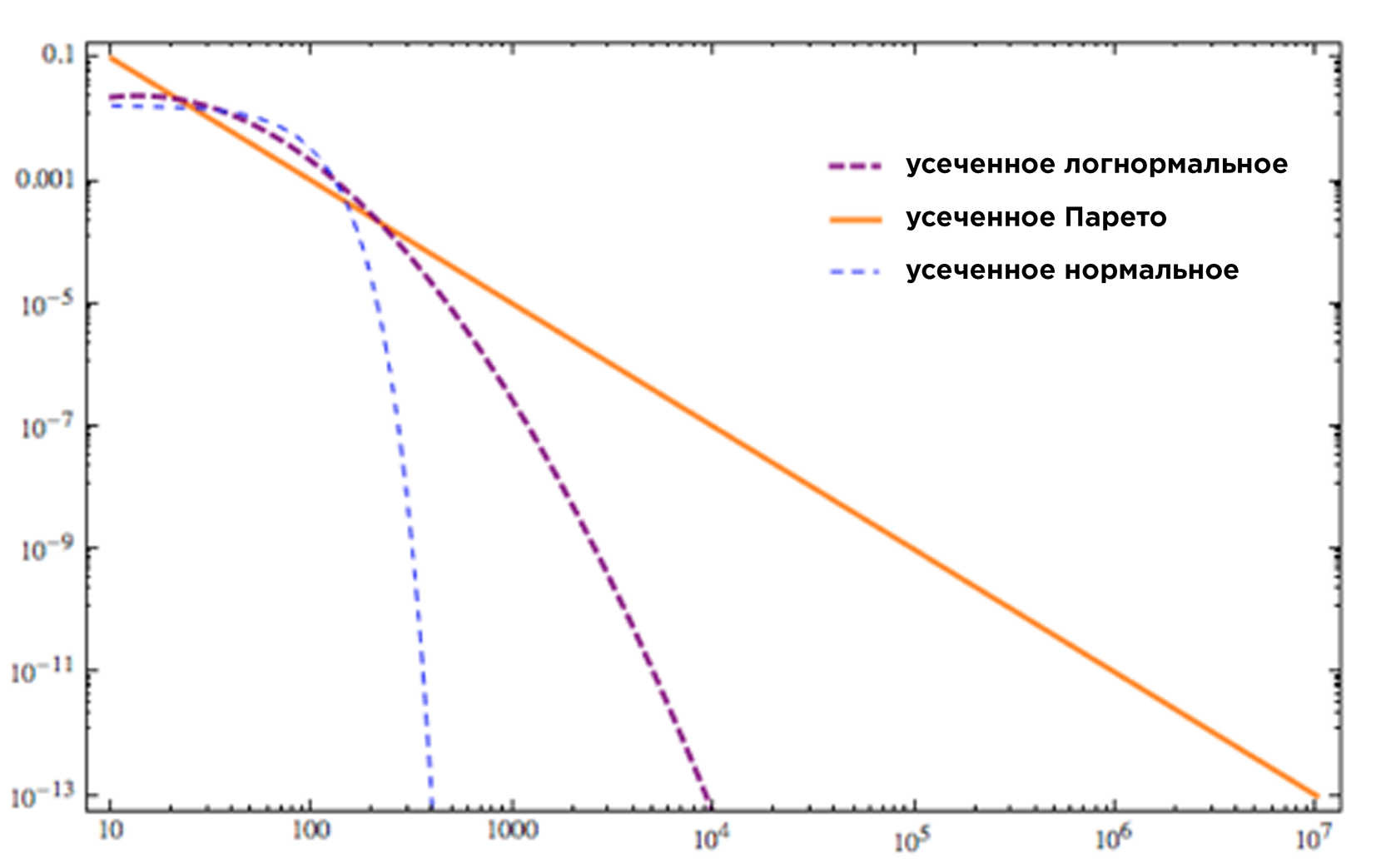
Выше много было сказано об указаниях на степенные распределения богатства. На самом деле, не всё так просто! До сих пор остается спорным, какой именно моделью удобнее описывать распределение богатства (Brzezinski 2013, Benguigui and Marinov 2015). Некоторые исследователи предпочитают модель логнормального распределения, другие даже предлагают использовать несколько моделей для описания разных участков распределения. Безусловно одно — реальное распределение благ имеет «тяжелый хвост», в отличие от тонких хвостов нормального распределения. Именно в «тяжелом хвосте» распределения благ находится меньшинство сверхбогатых.

Что-то не так с неравенством

Многие врожденные признаки людей распределены нормально.

Но распределение богатства совсем не похоже на нормальное!

Значит, между распределением врожденных свойств и распределением богатства есть что-то еще. Какое-то третье, опосредующее, звено.

Механизм, который превращает незначительные стартовые отличия в гигантское социальное неравенство.

Механизмы степенных распределений

Если нормальное распределение хорошо объясняется сложением множества незначительных по силе случайных факторов, то степенное распределение, вероятно, подразумевает некоторую доминирующую закономерность. Модели, способные генерировать степенные распределения свойств, показывают, какой могла бы быть эта закономерность.

Единого объяснения степенным распределениям нет. В самом деле, степенные законы обнаруживаются в самых разных сферах, включая биологию и физику — и вполне возможно, что для разных явлений, действуют разные механизмы (подробнее Newman 2006). Но есть несколько доминирующих теорий, которые принято использовать, чтобы объяснить степенные распределения в обществе.

Ниже мы поговорим о моделях «кумулятивного преимущества» и «самоорганизующейся критичности». Но чтобы перейти к этой теме, нужно сказать пару слов о распределениях свойств на моделях социальных сетей****.

Социальные сети и распределения

Модели вероятностных распределений используются для упрощенного описания больших систем — и в частности, комплексных сетей. Чтобы найти в сырых данных паттерн, вместо простого перечисления всех узлов и связей сети, можно рассмотреть распределение по сети отдельных свойств: например, степеней вершин, длины пути, коэфициента кластеризации. Это позволяет сравнивать распределение свойств в реальных сетях и в различных моделях сетей, чтобы сделать выводы о закономерностях, лежащих за структурой реальных сетей.

Давайте посмотрим на модели случайных сетей с разными паттернами распределения степеней вершин.

Здесь кончается первая серия текста. В следующей части: механизмы степенных распределений в математических моделях и данных антропологии.

_____________

* И. Ильин: «На самом деле люди не равны от природы и не одинаковы ни телом, ни душою, ни духом. Они родятся существами различного пола; они имеют от природы не одинаковый возраст, не равную силу и различное здоровье; им даются различные способности и склонности, различные влечения, дары и желания; они настолько отличаются друг от друга и телесно и душевно, что на свете вообще невозможно найти двух одинаковых людей ... И вот, кто отложит предрассудки и беспристрастно посмотрит на жизнь, тот скоро убедится, что люди неравны от природы, неравны по своей силе и способности, неравны и по своему социальному положению; и что справедливость не может требовать одинакового обхождения с неодинаковыми людьми; напротив, она требует неравенства для неравных, но такого неравенства, которое соответствовало бы действительному неравенству людей».

** Важно отметить, что измерения IQ нарочно приспособлены под нормальное распределение. Нормальное распределение интеллекта — это мейнстримовая точка зрения; в Интернете можно встретить предположение, что правдоподобнее измерения интеллекта, которые способны дать распределения с тяжелым хвостом. Это можно было бы объяснить тем, что «естественные» способности нормально распределены, но в процессе обучения может возникать петля положительной обратной связи, которая и дает тяжелый хвост. В отличие от распределения роста, для которого не существует подобного механизма.

*** Талеб в своей книге Statistical Consequences of Fat Tails, дает такой пример: представьте что мы выбрали двух человек из нормально распределенной по росту популяции и получили крайне маловероятное значение 4.1 для суммы их роста. Много вероятнее, что каждый из них будет иметь рост приблизительно 2.05, чем какой-то другой — скажем, 10 см и 4 метра. Другими словами. Вероятность, что величина выходит за три стандартных отклонения, будет 0.00135 (см. правило трех сигм). Вероятность, что случится два события с отклонением в три стандартных отклонения, будет 1.8 × 10^-6. Но вероятность, что величина отклоняется от среднего значения больше чем на шесть стандартных отклонений — 9.86 × 10^-10. Следовательно, вероятность, что случится два события на трех сигмах больше, чем вероятность одного события на шести сигмах. С другой стороны, представьте, что мы взяли из распределения богатства двух случайных людей, и выяснили, что их совместное богатство — 36 млн долларов. Много вероятнее, что нам попался богач, который владеет приблизительно 35,999 млн, и человек с имуществом в 1000 долларов, чем два человека, которые владеют по 18 млн долларов.

**** Понятие «социальная сеть» не следует путать с «социальными медиа»: сервисами типа Мастодон, Вконтакте, Фейсбук. Социальная сеть — это любое представление отношений между людьми в виде сети. Кроме того, распределение степеней не следует путать со степенным распределением!

Ключевые слова для самостоятельного углубления в тему:

распределения вероятностей, распределение Парето, закон Ципфа, степенной закон, кривая Лоренца, неравенство участия, центральные предельные теоремы, закон Гибрата, Bodley's power-elite hypotesis, power law, Zipf's Law, Lotka's law, Gibrat's rule, Matthew effect, Yule process, Pareto distribution, preferential acquisition, increasing returns, the rich get richer effect, preferential attachment, degree distribution, the central limit theorem.

Канал:

@AnarchyPlus