Логистическое уравнение и концентрация власти: модель с меняющимися равновесиями

Предупреждение! Этот текст не имеет прямой прикладной пользы. Мы не использовали реальные данные по уровню централизации. Кроме того, реальные процессы в обществе куда сложнее, чем можно описать подобным подходом. Формулы здесь нужны только как увлекательная игрушка, с которой можно экспериментировать. Однако, этот текст может пригодиться как материал для размышлений. Неосознанно мы зачастую думаем о социальных процессах, как будто они находятся в равновесии, или меняются линейно. Здесь предлагается, хотя и грубый, но все же слегка более сложный взгляд. Если вы видите формальные ошибки или у вас есть собственные идеи по поводу применимости подобных метафор, пожалуйста, не стесняйтесь писать в бота @AnarchyGoBot или в коллективный анонимный чат.

Спорный тейк о том, как можно думать о процессе централизации и концентрации власти:

Логистическое уравнение

Логистическое уравнение можно рассматривать, как простейшую модель процесса с положительной и отрицательной обратной связью, который переводит систему от изначального нестабильного состояния к некоторому равновесию. Вот оно:

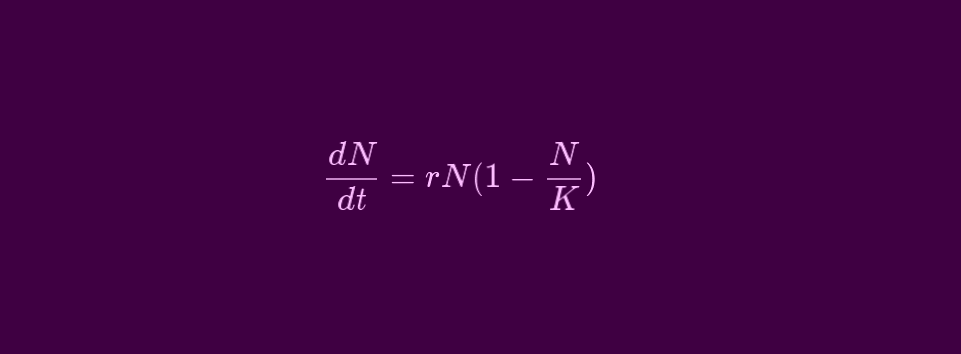
Выражение r*N изображает положительную обратную связь. Переменная N здесь — это значение параметра, изменение которого мы моделируем. Например, численность популяции или количество протестных акций. Постоянный коэфициент r определяет ускорение процесса. При r > 1, чем больше значение параметра N, тем быстрее оно будет расти.

Выражение в скобках 1-N/K изображает отрицательную обратную связь. Постоянная K определяет порог, приближаясь к которому, система приходит в равновесие. Когда K значительно больше N, значение 1-N/K близко к единице, и лишь незначительно тормозит положительную обратную связь r*N. По мере того как значение параметра N увеличивается, к единице стремится дробь N/K, и выражение 1-N/K все сильнее ограничивает рост параметра в r*N.

Важно отметить, что это крайне условное изображение обратной связи. Оно отражает лишь темпы ускорения и замедления процесса по мере роста значения параметра. Если бы мы хотели раскрыть реальные механизмы обратной связи, следовало бы смоделировать, каким образом возникает значение r и значение K. Или даже описать в модели более сложное поведение контуров обратной связи.

Вот так изображают график логистической функции:

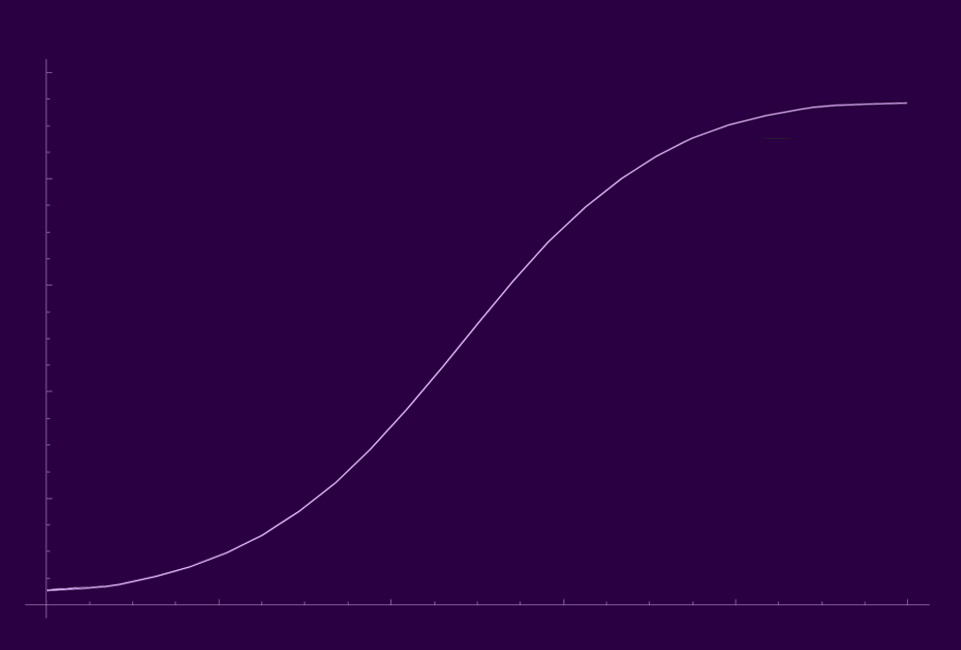
Положительная обратная связь выполняет роль «переключателя», который уводит систему от начального нестабильного состояния и приближает к равновесию. Отрицательная обратная связь делает систему устойчивой вокруг достигнутого равновесия.

Изначально логистическое уравнение использовалось для моделирования роста популяции в биологии. Но принцип, который оно описывает, настолько общий, что область использования этой модели можно расширить.

Экспонента, как высшая стадия капитализма

Существует два представления о накоплении власти и капитала.

Одно описывает процесс концентрации власти, как петлю положительной обратной связи: накопление стимулирует дальнейшее накопление. Ленин или Маркс описывали именно эту точку зрения. Конечно, в действительности ПОС не может действовать бесконечно, и в какой-то момент старая система разрушается, или переходит в новое состояние. В утопическом видении марксизма, это новое состояние приравнивается к «социалистической» диктатуре, которая заложит фундамент для коммунизма.

Второе представление говорит о существовании петли отрицательной обратной связи. Уровень концентрации власти не меняется значительно, он колеблется вокруг некоторого равновесия. Когда концентрация власти в системе превышает равновесный уровень, операции системы перестают быть эффективными, и концентрация власти падает. Если концентрация власти в системе ниже равновесного уровня, она растет, пока не достигнет этого уровня. Подобную точку зрения разделяет, к примеру, анархо-капиталист Д. Фридман.

Между этими взглядами нет существенного противоречия, если рассматривать их через описанную выше модель «переключателя» от изначального состояния системы к равновесию. Можно представить, что Ленин писал свои работы, когда график логистической функции концентрации капитала приближался к экспоненте. Затем значение параметра централизации стало ближе к предельному, и замедление централизации, а также крах слишком централизованных систем стали наглядным опытом.

Потолок сложности

Как складывается петля положительной обратной связи в концентрации власти? Неравные возможности конфликтующих групп позволяют доминирующей группе влиять на условия конфликта так чтобы еще сильнее увеличить неравенство возможностей. Вероятно, в какой-то момент, чем больше неравенство — тем быстрее растет неравенство.

Все, что для этого нужно — неустойчивость и стартовое неравенство. Некоторые антропологи предполагают, что выраженное социальное неравенство впервые появилось в связи со скачком сложности в человеческом обществе. Иерархические способы организации позволили организовать сложность, с которой не могли справиться горизонтальные техники организации.

Любопытно, что верхний порог концентрации власти, по всей видимости, тоже ограничивает социальная сложность. Слишком централизованные системы в слишком сложной среде не могут обработать все задачи, которые должны решать, чтобы сохранить контроль над средой. Появление крупных городов, рост населения, развитие доступных массам технологий и экспансия власти на новые территории — все это увеличивает сложность контролируемой среды*. Лекарством от краха систем управления становится относительная децентрализация. Если это верно, то уровень сложности системы задает окно эффективных способов организации, в частности — эффективной степени централизации.

Механизм отрицательной обратной связи, стабилизирующей рост концентрации власти, это нагрузка сложности на средства организации (здесь можно вспомнить закон необходимого разнообразия Эшби и его мультимасштабное применение у Бар Яма). Параметр K в нашей модели будет символизировать предельное значение централизации, после которого она не способна справиться со сложностью среды. Вокруг данного значения, будет колебаться уровень централизации.

Практический смысл K: сложность среды, выше которой организации, управляющие этой средой, неустойчивы.

Прерывистое равновесие

Самое время задаться вопросом: как именно складывается значение параметра K? Очевидно, он означает не сложность общества в каком-то абсолютном выражении, а взаимодействие абсолютного уровня социальной сложности и существующих технологий организации, которые позволяют эту сложность контролировать.

Это отношение меняется в процессе развития человеческого общества. Возникают новые технологии связи, обработки данных, социальных взаимодействий**. С новыми технологиями, потолок сложности поднимается. Частота появления новых технологий, в свою очередь, может зависеть от уже достигнутой сложности системы и сложности организации.

Тогда рост централизации в обществе в самом простом виде можно отчасти описать двумя выражениями, одно из которых — логистическое уравнение, показывающее переходы между разными равновесиями уровня централизации, а другое — функция, стохастически меняющая значение K в логистическом уравнении в зависимости от уже достигнутого уровня централизации и сложности общества с некоторой задержкой.

Когда текущее и равновесное состояния системы отличаются, включается механизм положительной обратной связи, и система стремится к равновесию, заданному K, где стабилизируется петлей отрицательной обратной связи. Каждый раз, когда значение K меняется, старое равновесное состояние оказывается нестабильным. Больше не подавляемая положительная обратная связь, заданная коэфициентом r, переводит систему из старого равновесия в новое.

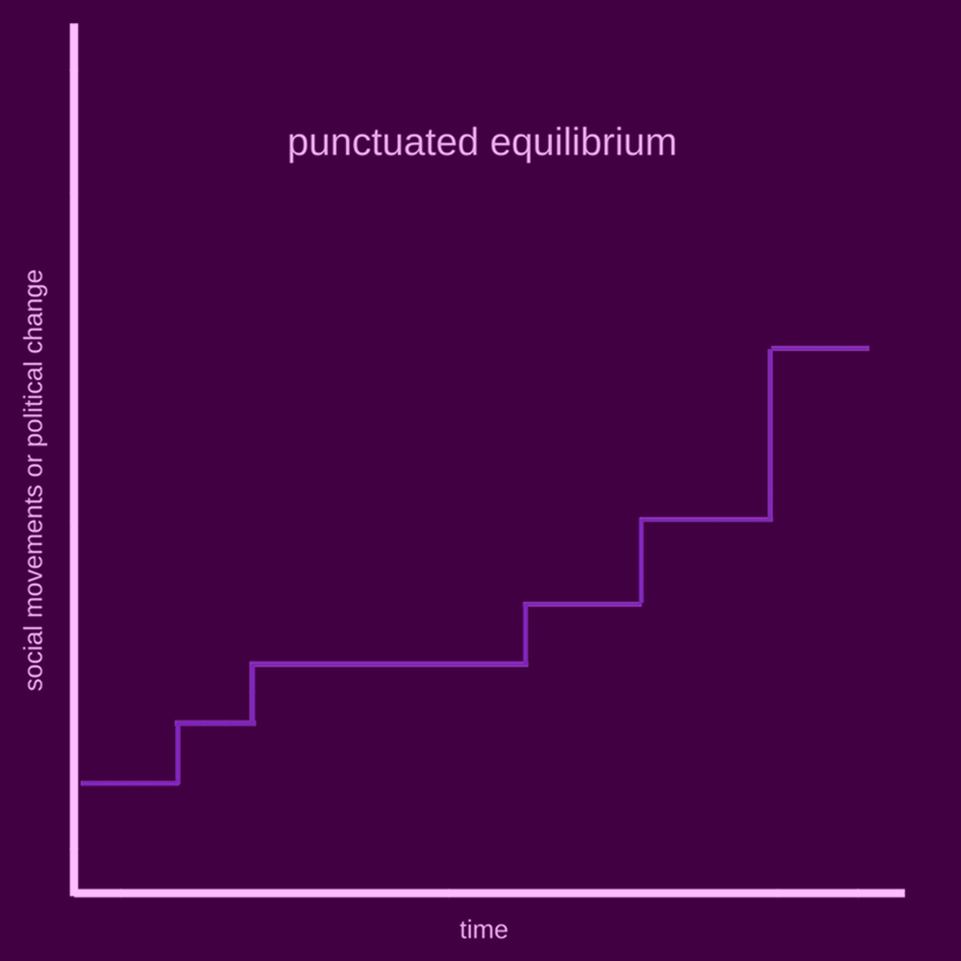
В зависимости от частоты изменения K, мы получим более или менее ступенчатый график процесса. Знакомая картинка: похожим образом схематически изображают «прерывистое равновесие» эволюции социальных систем. Но дело не только во внешнем сходстве графика нашей модели и графиков эмпирических данных. По всей видимости, во многих социальных процессах с s-образным графиком действуют петли положительной и отрицательной обратной связи.

Когда политический порядок находится в неустойчивом состоянии, протестные акции стимулируют новые протестные акции, и протест нарастает взрывообразно. Небольшие реформы в слишком жесткой системе повышают неопределенность, к которой жесткий порядок крайне чувствителен, неопределенность вызывает рост неопределенности, и это провоцирует каскад изменений.

Постепенно система приходит к равновесию — и остается в нем, пока условия равновесия не изменятся. Тогда система, которая была устойчивой еще вчера, внезапно становится нестабильной, и взрывная ПОС переводит ее к новому равновесию. Периоды рутинной стабильности чередуются периодами текучести. Подобную картину можно найти в разных социальных процессах***.

Впрочем, надо еще раз отметить, что изображение настолько сложных процессов через подобную простую модель несколько условно. Даже петли обратной связи в реальных социальных процессах множественны и работают по куда более сложным закономерностям.

Мета-централизация

На относительно небольшом участке времени, мы видим s-образную кривую, которая показывает, как процесс переходит от неустойчивого состояния к устойчивому. Но если взять больший масштаб, мы возможно увидим ступенчатое изменение процесса, где периоды быстрых перемен сменяются периодами стабильности. Куда интереснее, чем вопрос о текущем равновесном потолке централизации, был бы вопрос о том, по какой закономерности меняются условия равновесия, и куда нас это ведет в долгосрочной перспективе.

Это прямо касается проблемы устойчивости анархии. Все надежды на свободное общество равных связаны с некоторым балансом сил, который образует систему взаимного сдерживания и не дает расти концентрации власти. Примеры устойчивого существования таких систем известны. Даже современный уровень концентрации власти оставляет некоторую надежду. Но все эти стабильные состояния оказываются лишь метастабильностями, которые легко нарушаются при изменении некоторых сопутствующих условий.

Можно представить два выхода: либо стабилизировать второй контур изменений, который меняет условия равновесия, либо все время опережать в этой гонке, задавая условия нового равновесия так чтобы оно позволило анархическим системам сохраняться — бесконечный бег по лезвию.

_______________

Забавные детали:

*Это значит, что потолок сложности может не только подниматься, но и опускаться. Например, появление Интернета поначалу резко усилило значимость децентрализованных способов организации. Вопрос в том, что будет происходить быстрее.

**Впрочем, развитие технологий контроля также меняет сложность сообщества! Парадокс бюрократии: системы управления усложняются, чтобы справиться со сложностью среды, из-за чего сложность среды увеличивается, так как аппарат управления является ее частью.

***Логистическое уравнение хорошо описывает изменение численности популяций животных в стабильных условиях, но много хуже предсказывает изменение численности популяции людей. Возможно, это отчасти связано со все тем же изменением равновесных условий, которое могла бы изображать функция, задающая К: часть антропологов считает, что давление популяции (демографическое давление / polulation pressure) способно спровоцировать организационные изменения в обществе, а организационные инновации способны изменить емкость среды К (см. Organizational Structure and Scalar Stress by Gregory A. Johnson).

Мы добавили к словесному описанию простую математическую иллюстрацию, потому что это язык, который часто используется в литературе по важным для анархизма проблемам, и стоит постепенно привыкать проводить параллели между мат моделями и словесными моделями, от простого — к сложному.

Канал: @AnarchyPlus.