Тяжелые хвосты и нормальное равенство. Часть 2

@AnarchyPlus

Это вторая часть текста о распределениях и социальном неравенстве.

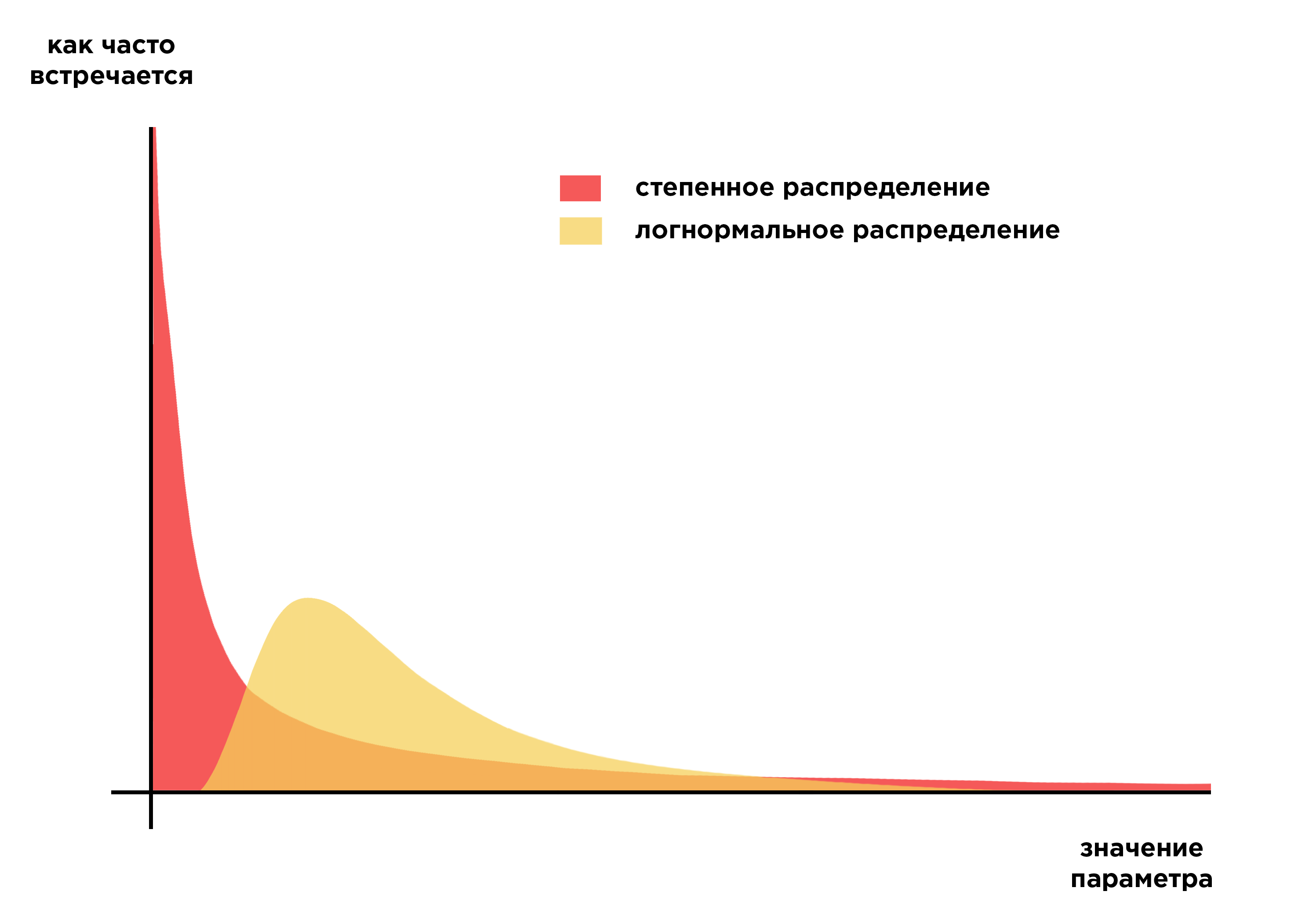
1. В природе часто встречаются распределения по нормальному закону. Рост и сила людей — нормально распределены. Но если в разговорах о распределении богатства и статуса вы представляли колокол нормального распределения, вы представляли неравенство неверно. Для социального неравенства характерны радикально отличающиеся распределения с тяжелыми хвостами. В частности — степенные распределения. Шок!

2. Остается спорным, насколько хорошо подходят для моделирования неравенства именно степенные распределения (а не другие распределения с тяжелыми хвостами). Однако, это удобная и простая модель, которая широко используется. На текущий момент степенные распределения можно рассматривать как «базовую» модель, для которой разрабатываются теоретические объяснения, и с которой можно сравнивать отклонения в конкретном наборе реальных данных с более-менее похожим паттерном.

3. Есть указания, что степенной закон действует скорее в тяжелом хвосте «богатых», а масса «бедных» распределена иначе — такие распределения называются «смешанными».

Ниже:

Как появляется степенное распределение, его конкурент — логнормальное распределение, и смешанные распределения. Если мы поймем, каким образом возникает неравенство с тяжелым хвостом, появится шанс выяснить, как этого избежать.

Пожалуйста, пишите о недостатках и ошибках на @AnarchyGoBot или в чат в закрепе, если бот не отвечает.

Блок 2 — продолжение

В прошлом тексте мы остановились на сетевых моделях.

Сложные системы, в которых множество элементов взаимодействует между собой, удобно представлять как сети (или «графы»). Узлы (или «вершины») изображают объекты, а связи («ребра») между узлами — взаимодействия. «Степенью» узла называется количество связей с другими узлами. Распределение степеней показывает, как часто встречаются узлы с тем или другим показателем степени (не следует путать распределение степеней и степенное распределение, degree distribution / power-law distribution). Разные типы сетей способны давать различные распределения.

Зачем это нужно знать?

В прошлой серии, нормальное распределение благодаря внезапному повороту сюжета оказалось связано с влиянием множества приблизительно равных по силе независимых факторов, а степенное — с некоторой доминирующей тенденцией.

Две разные модели генерации сетей отражают в точности эти свойства. Но так, что вы легко сможете провести параллели с социальными или другими сложными системами! Сетевые модели пригодятся нам в качестве инструмента, чтобы думать о разных распределениях свойств социальных систем.

Экспоненциальные и безмасштабные сети

Можно выделить две категории сетевых моделей, судя по распределению степеней узлов (Barabasi and Albert 1999).

В сетях первого типа, пик распределения степеней приходится на среднее значение, а затем экспоненциально убывает к большим и меньшим значениям. Примером может служить случайный граф Эрдёша-Реньи (Erdos and Renyi; ER model) или граф «мир тесен» Уоттса и Строгаца (Watts and Strogatz; WS model). Обе модели производят довольно гомогенные сети — то-есть, узлы в них имеют приблизительно одинаковое количество связей. Этот тип сетей можно назвать «экспоненциальными» сетями (exponential networks).

Если вы не понимаете, о чем речь — читайте первую часть

Сети второго типа крайне гетерогенны. Мода (пик) распределения приходится на низкие значения степеней: большинство узлов имеет мало связей с другими узлами. Но вероятность убывает к большим значениям степени узла по степенному закону, и справа лежит «тяжелый хвост» распределения. В отличие от экспоненциальных сетей, где вероятность найти узел со значительно большей степенью пренебрежительно мала, здесь, хотя и редко, но встречаются сильно нагруженные связями узлы (хабы). Такая сеть называется «безмасштабной» (scale-free). Примером модели этого класса может служить граф Барабаши-Альберта (Barabasi and Albert; BA model).

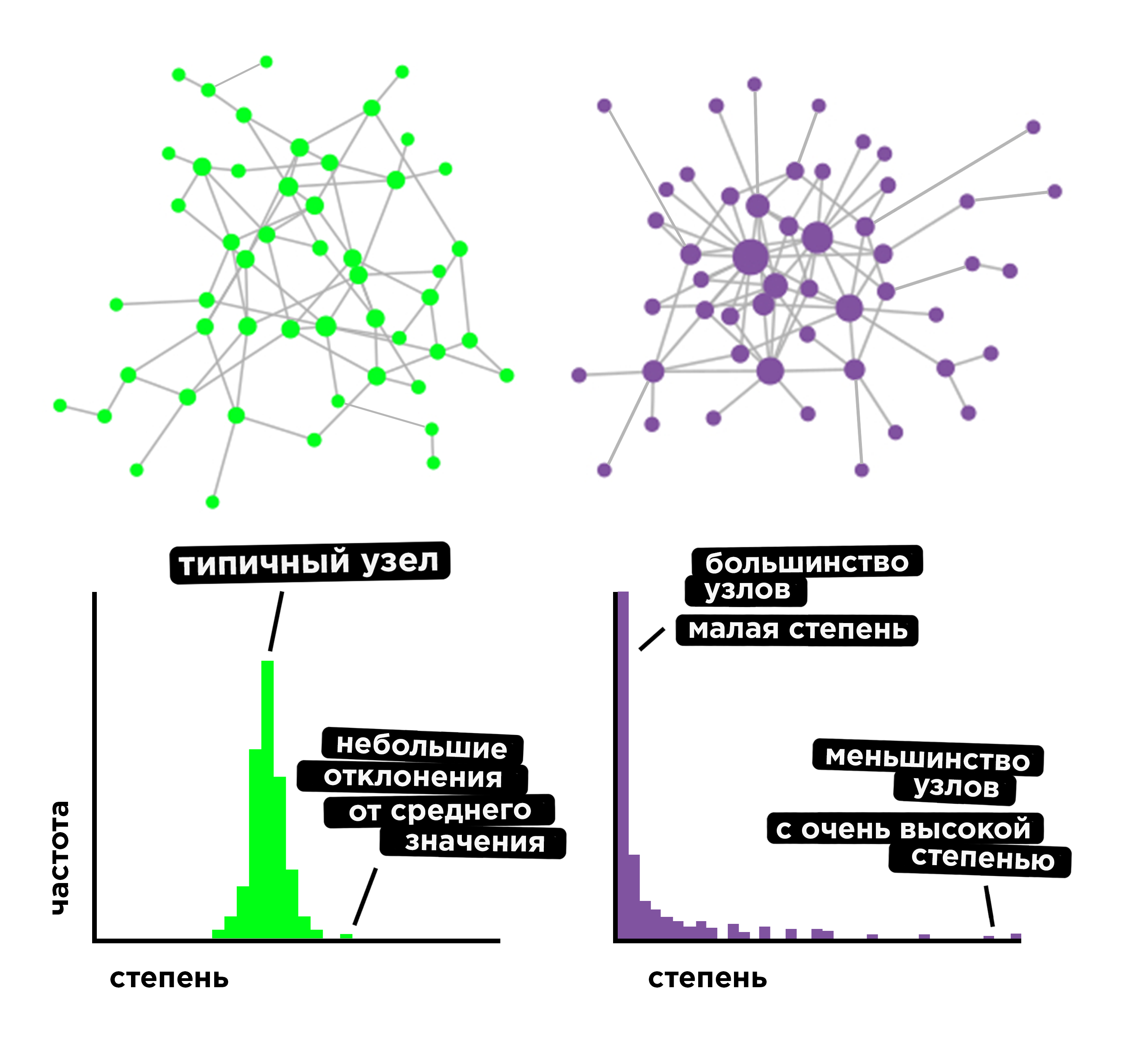
Помните, выше мы говорили об экспоненциальных и тяжёлых хвостах распределения? Здесь почти что повторяется сказанное в разделе «Тяжелые хвосты», только в этот раз речь идет о распределении степеней.

На картинке — схематическое изображение экспоненциальной и безмасштабной сети, а также распределений их степеней.

Многие исследователи находят в реальных социальных сетях степенные распределения степеней вершин. Социальные сети — это часто безмасштабные сети. Хотя после первой волны энтузиазма стали обнаруживаться и контрпримеры[1].

Напротив, граф Эрдёша-Реньи со временем стал считаться не слишком реалистичным представлением настоящих сетей общества — распределение степеней узлов в нем слишком «эгалитарно».

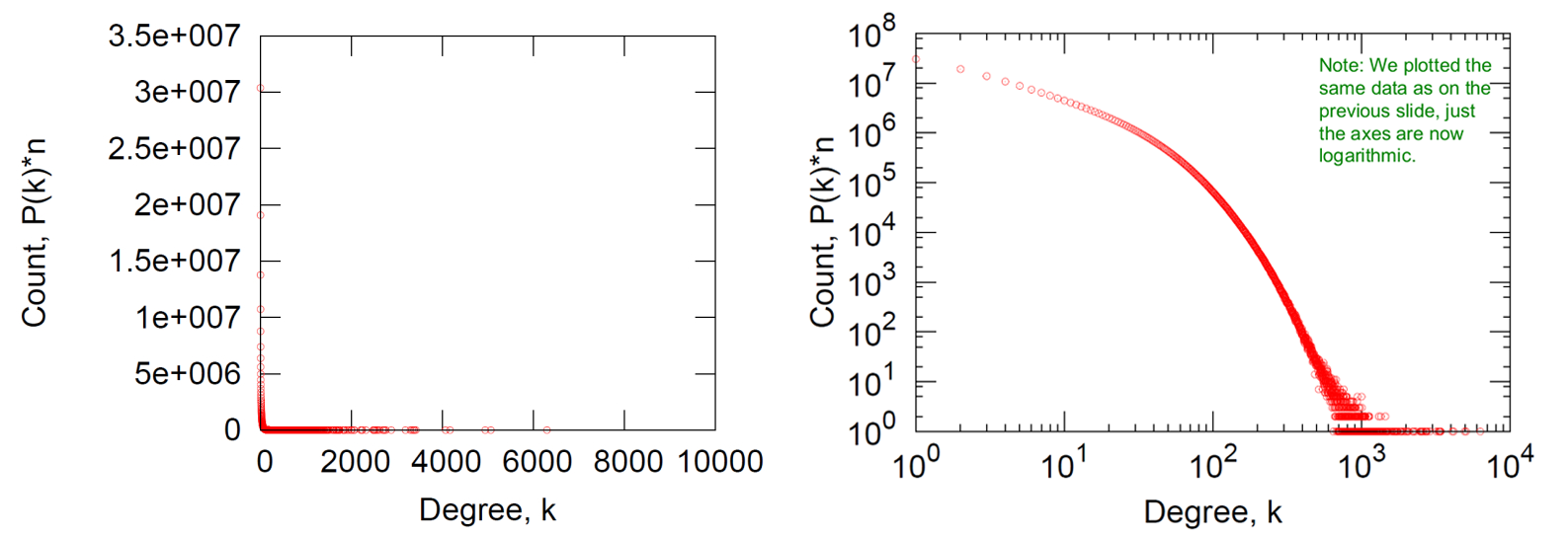
Распределение степеней (количества контактов) пользователей мессенджера MSN.
Слева: характерный паттерн распределения c _жирным и необрезанным_ тяжелым хвостом — если уместить все значения на обычной, не логарифмической, горизонтальной шкале, точки будто бы прижмутся к осям. Справа: те же данные в двойной логарифмической шкале. Как видно, паттерн не совсем похож на прямую степенного закона — возможно, это логнормальное распределение. Определить подходящую модель на глаз не всегда возможно, для этого есть специальные тесты. Источник: https://www.notion.so/Sberloga-with-Graphs-12fafe3224e1483eb435a16aa990e1a1

Случайный граф Эрдёша-Реньи

Модели каждого класса имеют свои специфические механизмы генерации.

В модели Эрдёша-Реньи, нам задано произвольное количество узлов n. С некоторой вероятностью p, между любыми двумя узлами возникает связь. С вероятностью 1−p, связи не возникает*. Это аналогично тому, как если бы степень одного узла определялась подбрасыванием монетки n−1 раз** (см. биноминальное распределение), причем нам потребуется «нечестная» монетка, которая чаще выпадает на одну сторону, если вероятность создания связи и вероятность, что связь не возникнет, не равны.

*Вероятности "р" и "1−р" это просто запись, которая показывает, что сумма вероятностей равна единице, т.е. одно из этих событий точно произойдет. Если р = 0.5, то и 1−р = 0.5. Если р = 0.9, то 1−р = 0.1. И так далее.

**Под "n" здесь имеется в виду общее число узлов. Записано "n−1" — потому что в этой модели узел не может создать связь с самим собой, и значит исключается из общего числа узлов, которые могут соединиться с ним с вероятностью "р".

При разных значениях параметров модели, получившееся распределение степеней может быть удобно представить как нормальное или похожее на него пуассоновское распределение. Здесь действует та же логика, что уже была описана выше: значение степени определяет большое количество независимых и примерно равных по силе случайных факторов.

Случайные сети ER для разного значения “p”.

Взято с https://ca.wikipedia.org/wiki/Fitxer:Erd%C5%91s%E2%80%93R%C3%A9nyi_model_random_graphs.pdf

Эта модель может быть интересна нам по двум причинам. Во-первых — потому что она часто используется как отправная точка для сравнения свойств различных более реалистичных моделей социальных сетей. Другая причина... к ней мы еще вернемся позже.

Модели для генерации безмасштабных сетей отличаются от модели ER — вероятность создания связи между любыми двумя узлами там будет не одинакова.

Накопление преимущества

Правдоподобным механизмом степенного распределения в социальных системах считается «кумулятивное преимущество». Это когда выигрыш увеличивает следующий выигрыш. Чем больше население города, тем больше новых жителей он притягивает. Чем известнее артист, тем известнее может он стать. В литературе этот принцип также известен под названием «богатые богатеют» (“rich get richer”).

В различных моделях, используются другие названия[2]: «процесс Юла» (Yule process) в честь исследователя Yule (1925), который пытался объяснить распределение числа биологических видов по родам; «закон Гибрата» (Gibrat's rule), как назвал его Simon (1955), исследуя распределение размеров городов, публикаций исследователей и некоторых других явлений; «предпочтительное присоединение» (preferential attachment) в модели безмасштабных сетей by Barabási and Albert (1999); «предпочтительное приобретение» (preferential acquisition) в работе Maschner and Bentley (2003); «эффект Матфея» (Matthew effect) у Merton (1993). «Кумулятивным преимуществом» (cumulative advantage) этот принцип назвал Price (1976), который впервые применил его к сетям, изучая распределение числа цитирований научных работ.

И хотя разные модели подразумевают разные математические формализации, они зачастую опираются на один и тот же лежащий в основе принцип.

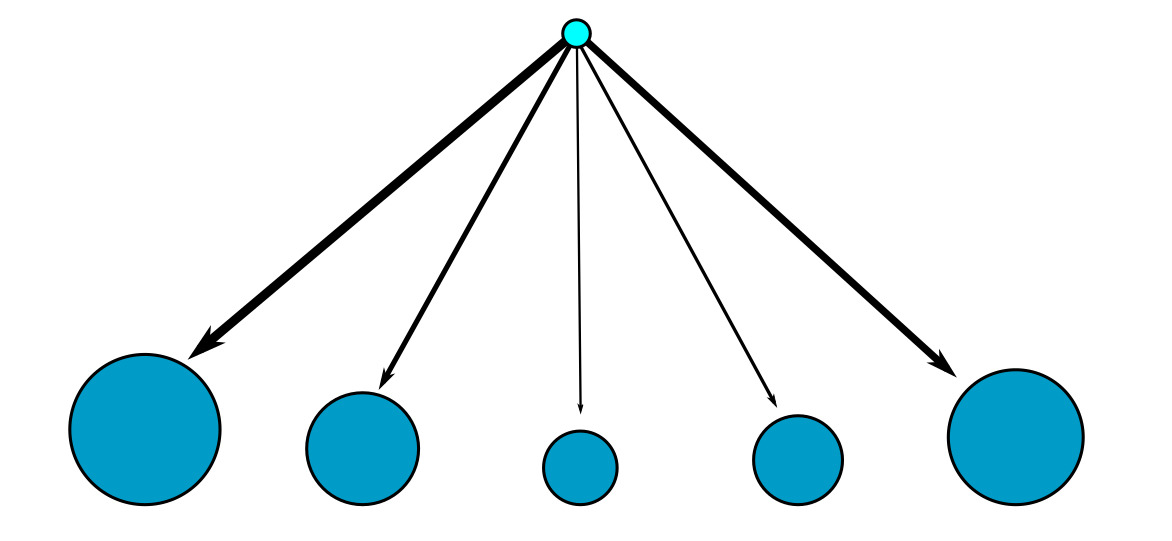
Представьте, что у нас есть некоторый набор объектов: городов, веб-страниц, капиталистов. Каждому объекту мы придаем некоторый «вес» — количество населения для городов, количество ссылок для страницы, размер капитала для рыночных игроков. Распределение показателей этого «веса» по множеству объектов может стать степенным, если темпы его роста для каждого объекта пропорциональны текущему «весу», так что чем больше «вес», тем быстрее он растет.

Ниже описаны два типа моделей кумулятивного накопления — предпочтительное присоединение и мультипликативные модели.

Предпочтительное присоединение (модель Барабаши-Альберта)

Barabási and Albert (1999) создали модель роста безмасштабной сети — то-есть, сети со степенным распределением степеней вершин (BA model)[3]:

В сеть по одному добавляются новые узлы. С некоторой вероятностью p, новый узел соединяется с любым другим узлом сети с одинаковыми шансами. С вероятностью 1−p, новый узел вместо этого скорее присоединится к большим узлам, с шансами, пропорциональными их размеру. Такая избирательность и называется «предпочтительным присоединением».

Принцип предпочтительного присоединения интуитивно кажется правдоподобным объяснением. К примеру, Интернет растет как безмасштабная сеть потому что чем популярнее сайт, тем вероятнее, что новый сайт сделает на него ссылку. Аналогично, если наиболее влиятельные люди с наибольшей вероятностью приобретают новые связи, возникнет безмасштабная сеть, в которой они станут самыми крупными узлами. Научная статья, которая часто цитируется, скорее будет обнаружена при поиске литературы, а значит, и скорее будет процитирована снова.

Схематически изображено предпочтительное присоединение. Только что добавленный красный узел мог прикрепиться к одному из бирюзовых с равной вероятностью, но следующий за ним сиреневый скорее присоединится к бирюзовому в центре, чем к каждому из других.

Итак, две ключевые концепции в модели BA это:

Рост сети (число узлов увеличивается со временем)
Принцип предпочтительного присоединения (узлы с большим числом связей чаще притягивают новые связи)

Эти две особенности можно наблюдать у многих реальных безмасштабных сетей. Контрольные модели, которые исключали хотя бы одно из этих свойств, дали другие паттерны распределения степеней узлов (Barabási and Albert 1999).

Власть и элиты

Похожий принцип лежит в основе гипотезы элиты Бодлея (power-elite hypotesis — Bodley, 1999). Хотя он не использует терминологию сложных систем, его выводы перекликаются с описанными выше особенностями безмасштабных сетей.

Bodley отмечает, что существует два условия, которые стимулируют рост неравенства, и это точно те условия, которые необходимы для складывания безмасштабной сети:

Рост экономики,
И способность элит получать больше преимуществ от этого роста

Мультипликативные модели (multiplicative process models)

Парето предполагал, что степенное распределение доходов может определяться неравным распределением способностей у людей. Логичным шагом будет представить «аддитивные» модели происхождения неравенства — где множество «особых способностей» суммируется, чтобы определить значение дохода. Но результатом такого процесса, как упоминалось выше, будет нормальное распределение величины дохода. С этой проблемой и столкнулись последователи Парето (Levy 2001).

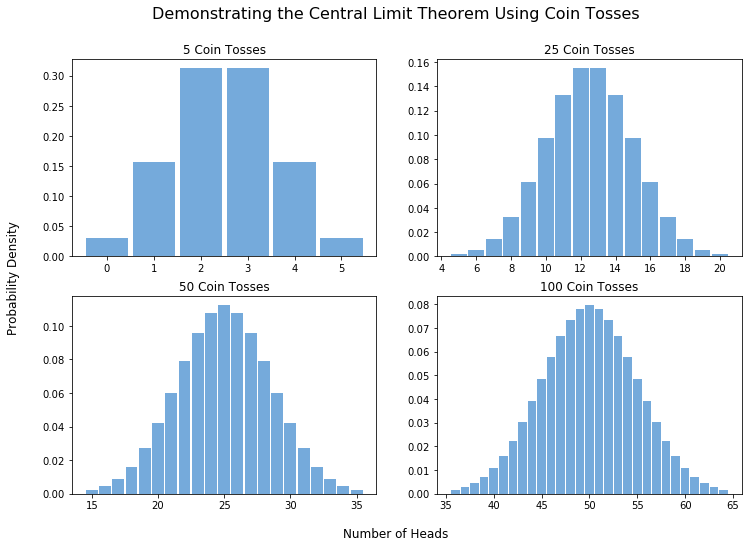
Представьте, что мы бросаем несколько монеток за раз. Орел — плюс один балл, решка — ноль. Выигрыши за один бросок суммируются. Мы получаем случайную величину, которая определяется рядом случайных факторов. График показывает, сколько раз сумма всех выигрышей за бросок принимала то или иное значение при множестве бросков. Если бросать одновременно достаточно большое число монеток достаточно долго, распределение величины сумм выигрышей будет приближаться к нормальному (см. биноминальное распределение). Помните модель Эрдеша-Реньи и как сложение множества случайных факторов дает колоколообразное распределение степеней узлов? Здесь то же самое.

Но что, если мы будем не складывать независимые переменные, определяющие значение нашей результирующей величины, а перемножать? Тогда мы получим распределение, которое будет иметь нормальный вид на логарифмических координатах. Это распределение с тяжелым хвостом, которое называется «логнормальным».

Здесь схематически изображена PDF логнормального распределения. Если горизонтальную шкалу сделать логарифмической, правый хвост распределения «сожмется» и график будет выглядеть как нормальное распределение. Поэтому распределение и называется логнормальным. Некоторые считают, что распределение благ на самом деле чаще бывает логнормальным, или смешанным — к примеру, логнормальное со степенным хвостом

Чтобы использовать эту особенность, осталось только найти в накоплении капитала процессы, где случайные факторы не складываются, а умножаются. И действительно, такие процессы есть. Прибыль в сделках может быть пропорциональна масштабу сделок[4].

Давайте не суммируем, а умножим результаты n независимых переменных. Чтобы избавиться от особенностей умножения на ноль и единицу (как в примере с монеткой), будем случайно брать значения переменных из равномерного непрерывного распределения между 0.5 и 1. Как и в прошлый раз, заносим результаты эксперимента на график. Чем больше n и больше количество экспериментов, тем больше график будет напоминать логнормальное распределение. Умножение результатов всех n случайных переменных за один эксперимент аналогично множеству последовательных шагов (числом n), в которых капитал одного участника рынка растет (или уменьшается) как произведение уже имеющегося капитала и одинаковой для всех участников вероятности выигрыша определенной доли. Количество экспериментов соответствует числу людей в популяции.

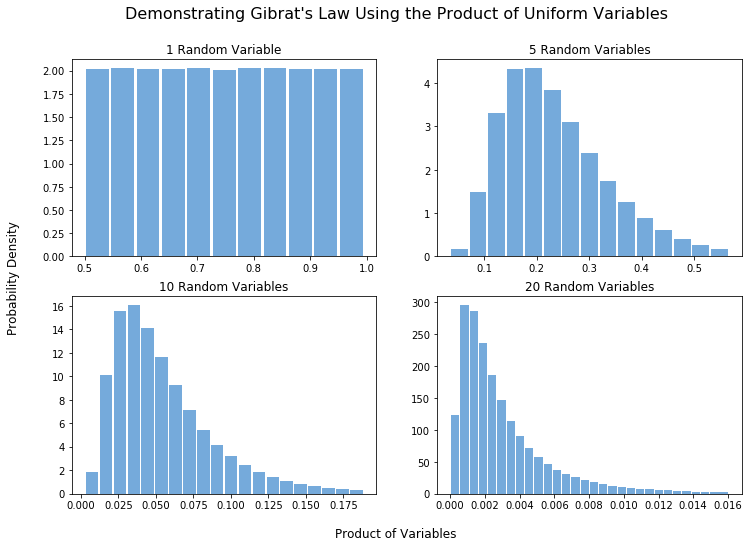
В общем виде, мультипликативная модель выглядит так. Есть множество объектов: городов, научных статей или участников рынка. С каждым шагом, объем уже накопленных каждым объектом ресурсов (жителей, цитирований, размера капитала) умножается на случайную переменную, так что объекты «выигрывают» или «проигрывают» ресурсы. Эта переменная не зависит от количества накопленного и принимает то или другое значение с одинаковой вероятностью для любых участников. Но если умножить в одинаковое количество раз большой капитал и маленький капитал, прибыль тоже будет отличаться пропорционально размеру капитала. Таким образом, чем больше ресурсов получил объект, тем больше будут его следующие выигрыши в случае удачи.

К примеру, Thomas (1967) предлагает мультипликативную модель для моделирования распределения размеров древних поселений, как пишут Maschner and Bentley (2003).

Базовая идея здесь та же, что и в модели «предпочтительного присоединения», но объекты накапливают не степень в сети, а абстрактный «ресурс».

Хотя в качестве безмасштабной сети можно представить совершенно различные системы — состоящие из людей, организаций, капиталов — модель предпочтительного присоединения ограничена тем что объясняет распределение именно степеней вершин. Не все величины удобно представлять в виде сетевого параметра.

Напротив, мультипликативные модели чуть более абстрактны, но потому налагают и меньше ограничений на то, какие действующие механизмы мы можем предполагать за явлением. Кумулятивное накопление здесь может возникать среди объектов, которые не связаны непосредственно.

Пафос таких моделей в том, что они показывают (Levy 2001):

Бедность или богатство могут определяться внешней случайностью, а не собственными качествами участников рынка
Неравенство с тяжелым хвостом возникает даже на «эффективном рынке», где нет информационных асимметрий, а шанс выигрыша в начале равен для любых участников

А что же со степенными распределениями в мультипликативных моделях? Некоторые модели со специфическими условиями дают не логнормальное распределение, а степенное (Champernowne 1953; Levy 2001). Есть и другая тонкость. Если колоколообразная кривая логнормального распределения достаточно сильно «растянута» на нашем логарифмическом графике (распределение обладает большой дисперсией и низким коэффициентом эксцесса), на небольшом участке ее может быть сложно отличить от прямой степенного распределения.

В следующей серии:

Больше о кумулятивном преимуществе. Данные антропологии, аналогии с кибернетикой, динамика успеха и ловушка бедности. Генерация смешанных распределений субтермальными и супертермальными классами дохода. После мы вспомним о катастрофах в накоплении капитала и поговорим о самоорганизующейся критичности.

Канал: @AnarchyPlus.

___________

[1] Возможно, типичная социальная сеть не будет безмасштабной. Похожим образом, со временем исследователи поставили под вопрос степенные распределения богатства, и сейчас многие описывают их более сложными моделями. Распределение степеней также может зависеть от того, связи каких субъектов мы измеряем — людей или фирм или аккаунтов, и контакты какого рода: знакомства, деловые или ресурсные связи. Дело в том, что иерархическая структура смягчает неравное распределение индивидуальных степеней, и анализ может определяться тем, принимаем ли мы в рассчет отдельных людей внутри иерархии, или целые сегменты иерархии. Предположим, что распределение степеней в социальной сети все равно будет иметь «тяжелый хвост». Знаете об этом больше? Напишите нам.

[2] Больше ключевых слов здесь: http://www.columbia.edu/~tad61/CA_AR112205.pdf (DiPrete and Eirich 2005). Сам Гибрат звал это “the law of proportionate effect”.

[3] Также см. модель, которая дает и степенное распределение степеней и «структуру сообществ» (community structure), которую часто можно наблюдать в реальном обществе: Kumar et al., “Stochastic Models for the Web Graph”, 2000. Фишечка этой модели — «копирующий механизм».

[4] Могут ли «перемножаться» особые способности? Некоторые исследователи в прошлом (как Boissevain, 1939) допускали такую возможность. Однако неясно, каким образом тут действует мультипликативный процесс. Кроме того, такое объяснение избыточно там, где мультипликативный процесс присутствует в самом движении капитала. В результате, эта теория так и не стала мейнстримовой. Скорее всего, не взаимодействие способностей определяет пропорциональное накопление капитала, а наоборот — сумма способностей дает стартовое «нормальное» неравенство, которое затем усиливается каким-то кумулятивным процессом. Например, тем что бо́льшие сделки дают шанс на бо́льшие прибыли. Впрочем, существует гипотеза степенного распределения эффективности труда (O’Boyle and Aguinis, 2017) — однако именно нижняя часть распределения доходов с оплачиваемым трудом обычно не вписывается в степенную модель. Поэтому, степенное распределение эффективности еще не объяснило бы степенного распределения доходов. Напротив, степенное распределение эффективности, если оно будет подтверждено, может оказаться одним из многих незначительных факторов, определяющих размер дохода, и тогда результатом могло бы быть нормальное распределение, если бы на первый план не вышли какие-то другие закономерности.

Ключевые слова:

random networks, scale-free networks, preferential attachment, предпочтительное прикрепление, предпочтительное присоединение, stochastic multiplicative process, Kesten's process, процесс Кестена, Lotka's law, закон Лотка.