Телефонный звонок (#94)

Решение

Пусть население города конечно и равно n. По условию задачи каждый житель сделал не более одного звонка, поэтому число звонков в городе не более чем n. Если бы каждый житель города разговаривал не менее чем с тремя жителями, то число звонков в городе было бы не менее 3n/2. Стало быть, обязательно найдётся житель, разговаривавший не более чем с двумя жителями.

Теперь доказательство требуемого утверждения легко провести индукцией по численности населения города n. База индукции n = 2 очевидна. Сделаем переход индукции. Выберем жителя А в соответствии с сделанным замечанием: житель А разговаривал не более чем с двумя жителями. Численность населения города без жителя А составляет n – 1, поэтому по предположению индукции его можно разбить на три группы с соблюдением требования задачи. Так как житель А разговаривал не более чем с двумя жителями, то его можно поместить в ту группу, которая не содержит его собеседников. Таким образом мы разобьём всё население города на нужные три группы.

Решение. Бесконечное число жителей

Без ограничения общности можно считать, что граф с вершинами-жителями и рёбрами-звонками является связным.

Возьмём произвольного жителя А0 и рассмотрим множества

Н0(А0) = {А0}

Н1(А0) = {X : житель X звонил жителю А0}

Нn+1(А0) = {X : житель X звонил кому-то из Hn(А0)}

H(A0) = H1(A0) ∪ H2(A0) ∪ … ∪ Hn(A0) ∪ …

I. Если житель А0 никому не звонил, то разобьём население города на две группы так. К первой группе отнесём совокупность жителей Нn(А0) с чётными номерами n:

H0(A0) ∪ H2(A0) ∪ … ∪ H2k(A0) ∪ …

а ко второй – с нечётными:

H1(A0) ∪ H3(H0) ∪ … ∪ H2k+1(A0) ∪ …

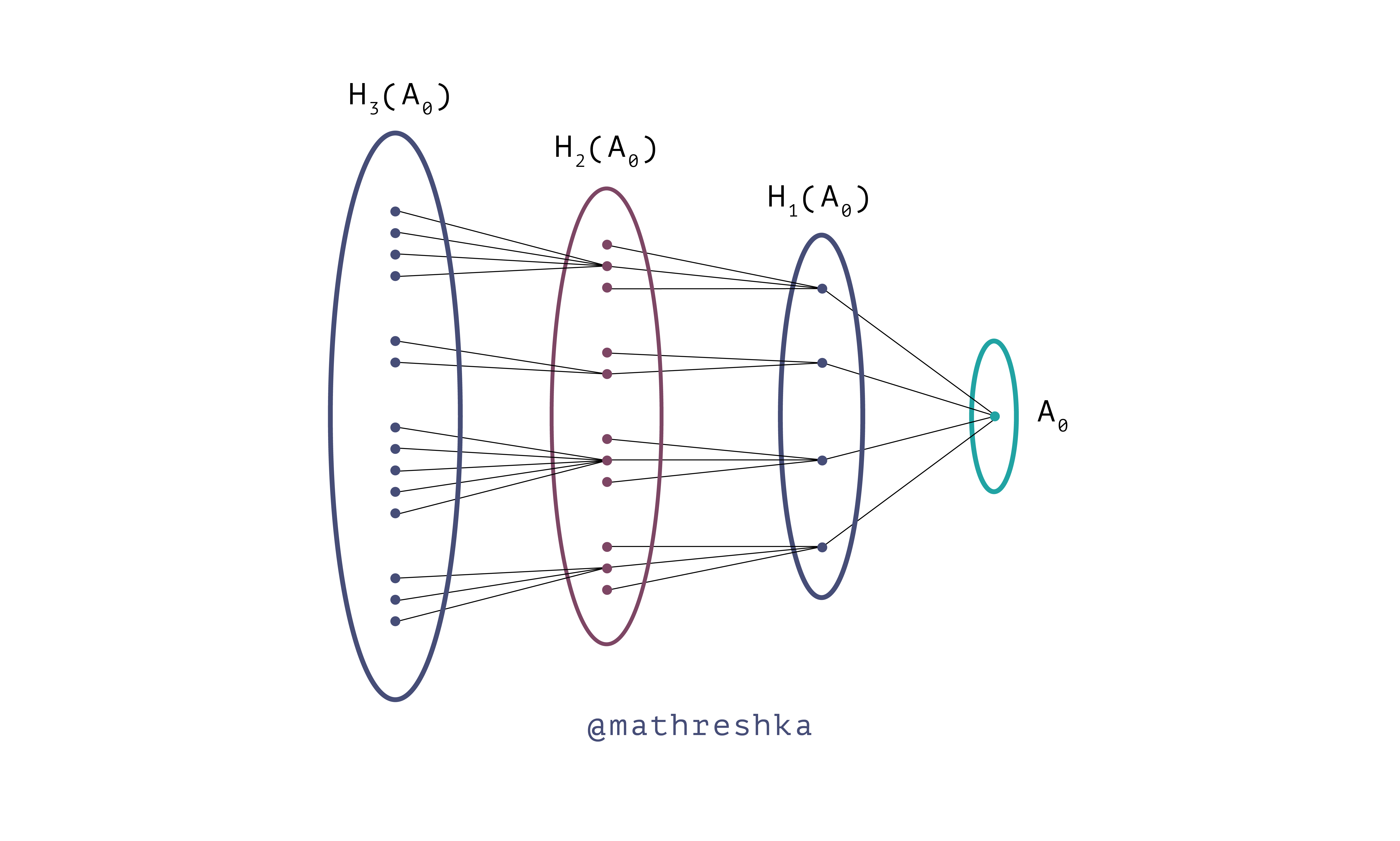
II. Если житель А0 звонил кому-то из множества Н(А0), то разобьём население на три группы так. К первой группе отнесём жителя А0, ко второй группе – совокупность жителей

H1(A0) ∪ H3(H0) ∪ … ∪ H2k+1(A0) ∪ …

к третьей

H2(A0) ∪ … ∪ H2k(A0) ∪ …

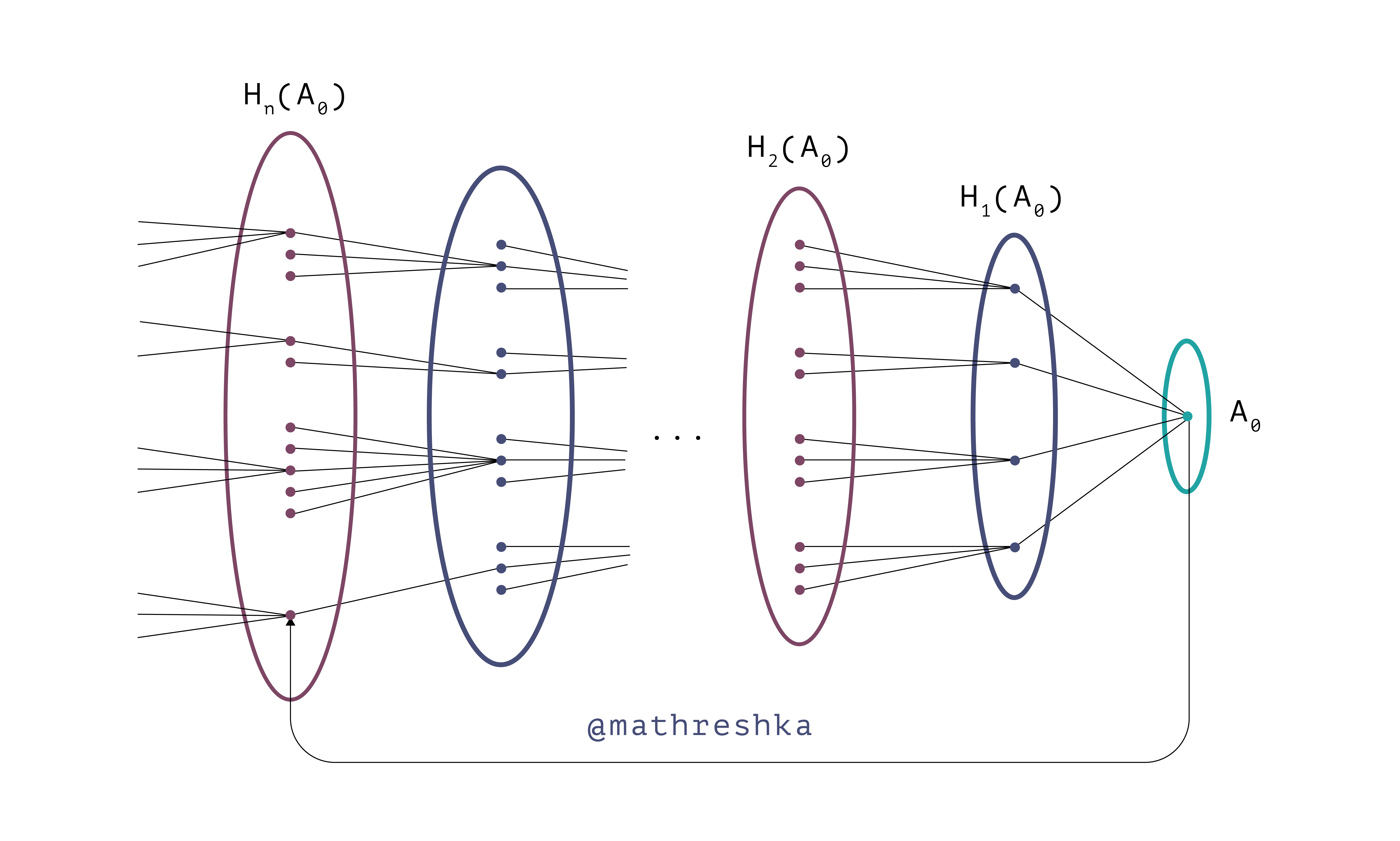
III. Если житель А0 звонил некоторому жителю A1 не из множества Н(А0), то рассмотрим множество H(A1) и повторим пункты I и II. Если всё время будем доходить до пункта III, то это будет означает, что всё население представляется в виде объединения

H(A0) ∪ H(A1) ∪ … ∪ H(An) ∪ …

Разобьём его на две группы следующим образом. К первой группе отнесём совокупность жителей

P0,0 ∪ P0,2 ∪ P2,0 ∪ P0,4 ∪ P4,0 ∪ … ∪ P2k,0 ∪ P0,2k ∪ …

ко второй группе

P0,1 ∪ P1,0 ∪ P0,3 ∪ P3,0 ∪ … ∪ P2k+1,0 ∪ P0,2k+1 ∪ …

где

Pi,j = Hi(Aj) ∪ Hi+1(Aj+1) ∪ Hi+2 (Aj+2) ∪ … ∪ Hi+n(Aj+n) ∪ …

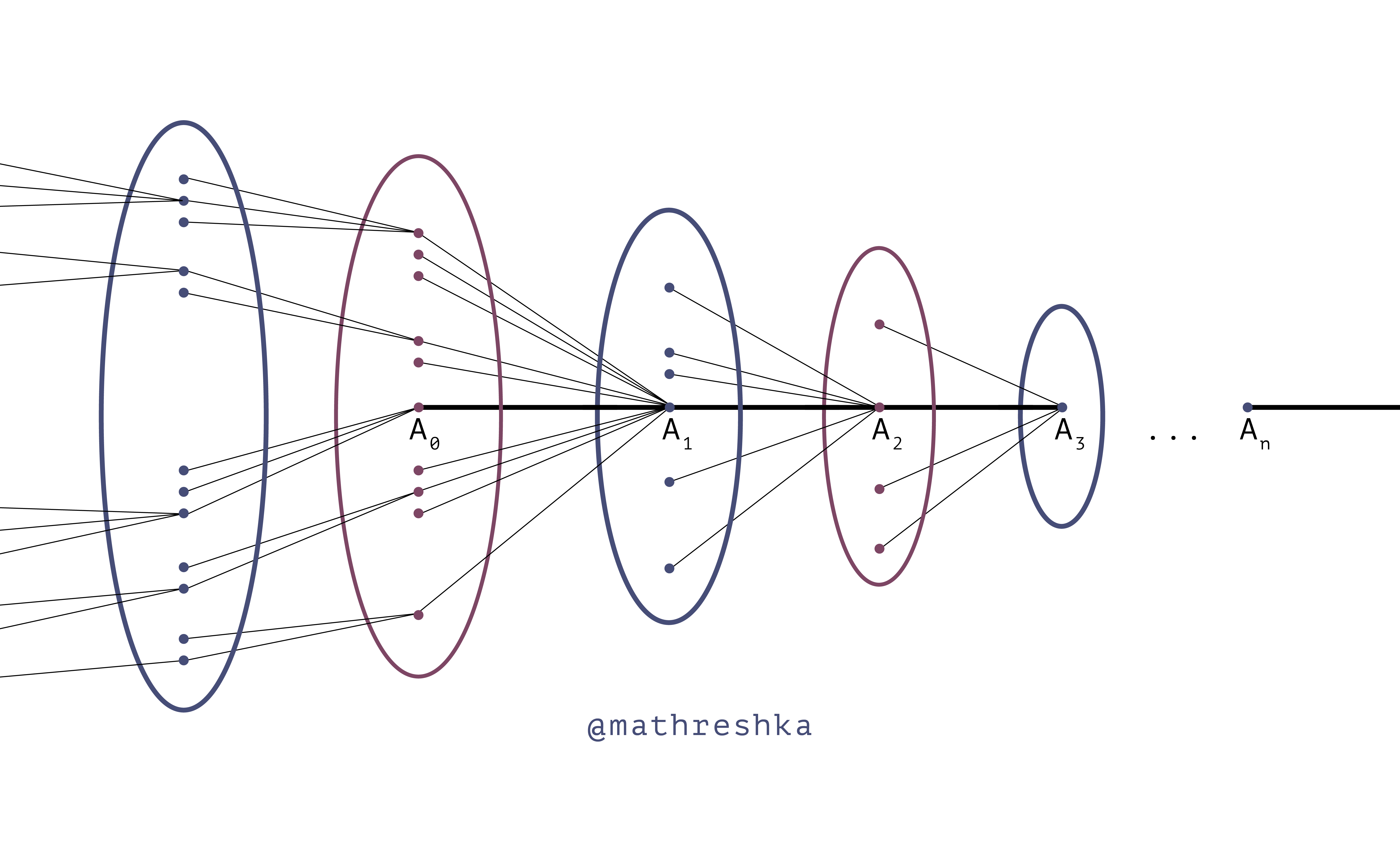
На рисунке множества Pi,j это в точности вершины, организованные в столбцы.

Условие  
Telegram