Решение. Доска 5x5 (#127)
MathreshkaОтвет: нельзя
Решение
Покажем, что мы всегда можем найти два столбца и две строки, на пересечении которых четвёрка клеток раскрашена в не более, чем два цвета.
Обозначим цвета 1, 2, 3, 4.
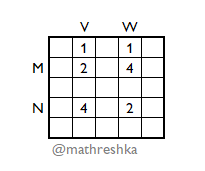
Рассмотрим первую строку. В строке пять клеток, поэтому найдутся хотя бы две клетки одного цвета. Пусть эти клетки стоят в столбцах V, W и покрашены в цвет 1.
Пусть теперь пара клеток, стоящая в столбцах V, W на пересечении со второй строкой, покрашена или в цвета (2, 3) или (2, 4) или (3, 4). Любой другой набор цветов сразу же приводит к искомой четвёрке клеток.
Аналогично, с третьей, четвёртой и пятой строками. Но вариантов раскраски три, а количество строк – четыре, следовательно, в каких-то строках, обозначим их M и N, набор цветов совпадёт.
Таким образом, клетки, стоящие на пересечении столбцов V, W и строк M, N, окрашены в два цвета.