Середні величини, так як розоритись через сліпе використання середнього арифметичного

Ця тема звучить певно найпростіше з усього, що я писав до цього часу. Колись я хотів написати по ній МАН (але знайшов щось куди більш творче), адже як виявилось, з такого простого поняття можна висмоктати купу розуміння (інсайтів, по модному). Для затравки:

Якщо ваше портфоліо виросло на 50% за перший рік, а потім скоротилось на 40% за другий, то на скільки в середньому воно росло за два роки? Відповідь: в середньому скорочувалось на приблизно 5%.

Нехай ми спостерігаємо зоряне скупчення, де половина зір має зоряну величину 5m, і ще половина -- 7m. Яка середня зоряна величина зір у скупченні? Відповідь: точно не 6m.

Почнемо з найпростішого -- середнього арифметичного.

Середнє арифметичне в кожну дірку

Що це взагалі за величина така і звідки вона береться? Вам всім відома формула:

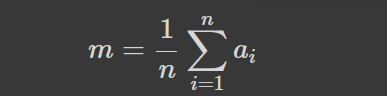
Проте можливо ви не замислювались, що її можна переписати у наступному вигляді:

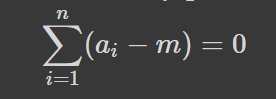
Зміст цього -- сума відхилень значень від середнього рівна нулю, себто середнє є в певному сенсі рівновіддаленою величиною. Тепер ще простіший запис:

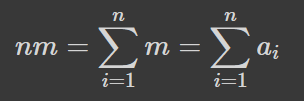
Фактично він означає наступне. Припустимо, у нас є набір числових даних, як от рівень річки протягом кількох днів, кількість написаних постів щотижня протягом кількох місяців, кількість хв проведених в інсті щодня абощо. Ми хочемо стиснути цей набір даних в одне число, яке збереже інформацію про кумулятивний ефект. Для цього ми замінюємо кожний запис (entry) на одну й ту саму величину так, аби їхня сума лишилась такою ж. Можна, звичайно, зберігати просто суму, але середнє є інтуїтивно зрозумілішим, а також зручнішим. Наприклад, якщо в середньому ми проводимо в інсті 5 хв на день, то ми можемо одразу отримати з цього 35 хв на тиждень і 2.5 год на місяць. Якби ми захотіли зберегти сумарний час за 5-денне спостереження, то для таких обчислень нам потрібно було б цей час поділити на 5 і помножити на тривалість, що і так приводить до поняття середнього арифметичного та змушує додатково пам'ятати кількість днів, протягом яких ми робили початкові спостереження. Дуже зручна величина, як на мене. Єдина незручність: для оновлення середнього значення при надходженні нових даних ми повинні використати кількість даних з попередньої вибірки, адже:

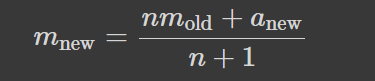
Середнє зважене

Останню формулу, до речі, можна трактувати як середнє зважене двох величин: старого середнього з вагою, яка рівна розміру старого набору, та нового спостереження з вагою 1. Якщо нових спостережень кілька, то це буде середнє зважене старого середнього та середнього серед нових даних з відповідними вагами. Середнє зважене можна розуміти і просто як кожний запис, повторений стільки разів, скільки його вага, проте для дробових ваг цей зміст не працює. Формула:

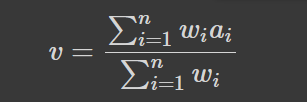
Наприклад, якщо у вас є кілька вимірів однієї величини x_i з різними похибками s_i, то середнє цієї величини обчислюється як:

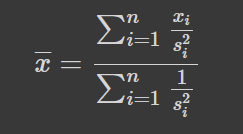
Імовірнісний, фізичний, та геометричний змісти

Середнє арифметичне має ще одну цікаву властивість -- воно мінімізує суму квадратів відхилень від наведених точок. Якщо присвоїти кожному доданку у цій сумі певну вагу, то отримаємо, що цією властивістю володіє вже середнє зважене. Наприклад, розглянемо ситуацію з вимірюваннями, знехтувавши систематичною похибкою. Зазвичай припускається, що випадкова (абсолютна, не відносна) похибка, отримана у процесі вимірювання, має нормальний розподіл з середнім рівним нулю (ненульове середнє можна змоделювати через ненульову систематичну похибку) та дисперсією, яка рівна середньоквадратичному (пояснено нижче) значенню похибки. Тоді густина розподілу випадкового вектору абсолютних похибок запишеться так:

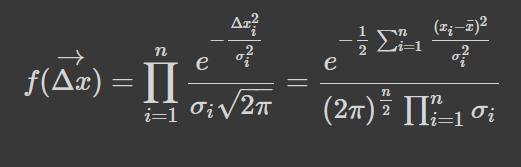
Далі, згідно з методом максимальної правдоподібності, цю густину ймовірності потрібно максимізувати відносно середнього, що означатиме максимальну ймовірність отримати саме такий набір даних, який у нас є. Мінімізація і надасть вищенаведену формулу з вагами, які рівні оберненій варіації (квадрату дисперсії).

У фізиці важливу роль відіграє поняття центру мас, наприклад у феноменах, пов'язаних з обертаннями та обертальними коливаннями, а також у механіці для відділення поступального руху системи як цілого від внутрішнього. Наприклад, координата центру мас визначається як середнє зважене координат кожної складової з вагами, рівними масам складових. Це призводить до того, що момент сил у однорідному полі тяжіння відносно центру мас рівний нулю, тобто не може повернути тіло. Віднімання ж руху центра мас від загального руху системи дозволяє звести задачу двох тіл до руху одного тіла у центральному полі тяжіння.

Більше того, момент інерції тіла відносно довільної осі обертання визначається як сума моменту інерції тіла відносно паралельної осі, яка проходить через центр мас, та mr^2, де r -- відстань між осями -- теорема Штейнера. З цього автоматично випливає, що момент інерції відносно осі, яка проходить через центр мас, у тіла є найменшим можливим, а отже його найлегше відносно цієї осі обертати.

Остаточно, через лінійність середнього, однорідні тіла чи їхні однорідні частини в багатьох (але не всіх) задачах можна замінювати на матеріальні точки з такою ж масою. Ба більше, центроїд трикутника можна знайти як центр трьох однакових мас у його вершинах, або центр мас вершини та вдвічі важчого відрізка на протилежній стороні, що й дає відоме співвідношення поділу медіани центроїдом у відношенні 2:1. Аналогічно можна отримати співвідношення для медіан (не апофем) трикутної піраміди 3:1, проте для піраміди з багатокутною основою (більше 3 вершин) цей метод ламається, напевно внаслідок порушення симетрії чи нестрогості.

Матсподівання та середнє континуальних величин.

Пригадайте означення матсподівання. Це середнє зважене значень випадкової величини з вагами, які рівні ймовірностям. Проте чому, і в чому зміст цієї величини? Пригадайте зміст середнього як стиснення кумулятивної інформації та зміст ймовірності. Припустимо, ви проводите дуже велику кількість експериментів n з випадковою величиною x. Тоді, згідно з означенням ймовірності, величина набуватиме значення x_i в n_i=np_i випадків, і матсподівання перепишеться як:

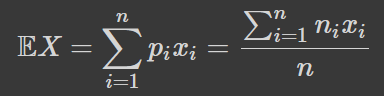
Тобто матсподівання є звичайним середнім, яке ви можете застосовувати для розрахунку кумулятивного ефекту. Чи дає воно вам уявлення про конкретний експеримент? Хороше питання, до якого ми ще повернемось.

Поняття середнього зваженого дозволяє нам поширити його на неперервний випадок:

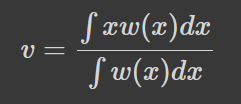
Кумулятивний же зміст середнього дозволяє означити середнє певної функції на проміжку:

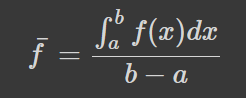
Що має зміст середньої висоти графіка, який дасть таку ж площу, прямокутника з даною основою, яку дає графік. Задамось тепер питанням: де знаходиться точка, яка дає це середнє значення функції? Два вищенаведених значення можна узагальнити в середнє (зважене) функціональне наступним чином:

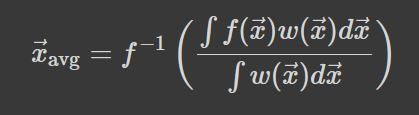
Це означення працює для довільної інтегровної багатовимірної функції. Для просунутості я мав би замінити вагу на міру, але досі не розумію що таке та міра. Зніміть вектор -- і отримаєте означення для функції однієї змінної. Зробіть вагу однорідною -- і отримаєте середнє функціональне. Замініть змінну на дискретну, і отримаєте квазі-арифметичне середнє, або ж середнє за Колмогоровим. Зміст у них такий самий, який ми наводили з самого початку: сума відхилень від значення функції в середній точці рівна нулю:

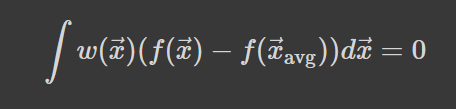
Заміна вагової функції на густину, а f(x) на х дає вираз для координати центру мас тіла з даним розподілом густини в кожній точці.

А як же інші середні?

Найпростіше після цього задатись питанням: що як ми хочемо отримати рівновіддалений квадрат величини? Це призведе до означення середнього квадратичного:

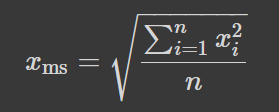
Яке, наприклад, відіграє першочергову роль у оцінці похибки випадкової величини з наведених даних -- дисперсія це середнє квадратичне відхилень від середнього, домножене на коректуючий коефіцієнт, який залежить від n:

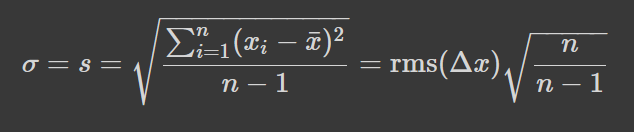
В межаз цього посту вважатимемо сігму та ес рівними. rms=root mean squared, тобто корінь і середнього квадрату величини. Середнє гармонійне означається ж через f(x)=1/x. Наприклад, середня густина бруска з кількох, однаково масивних частин, є середнім гармонійним густин цих частин. Узагальнюючи, означимо середнє степеневе:

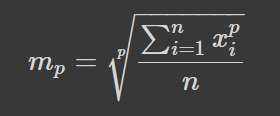
З нерівності Єнсена, можливо, можна показати, що чим більше р, тим більше середнє. Вона, до речі, є дуже корисною, і застосовує поняття середнього арифметичного. Для опуклої вниз функції, як от степеневої з p>1 (та р<0 і додатніх аргументів):

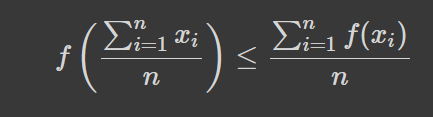
Нерівність можна довести за допомогою методу математичної індукції. Для опуклої вниз функції ми лише змінюємо знак.

Тож, можна здогадатись, що відбувається в цікавих випадках, як от р рівне плюс-мінус нескінченності та нулю. Для нескінченного ступеню достатньо винести за корінь найбільше число серед всіх і побачити, що середнє степеневе у цьому випадку рівне максимуму. Для мінус нескінченного, після аналогічної операції, отримуємо мінімум. Для нуля ж ми робимо наступне:

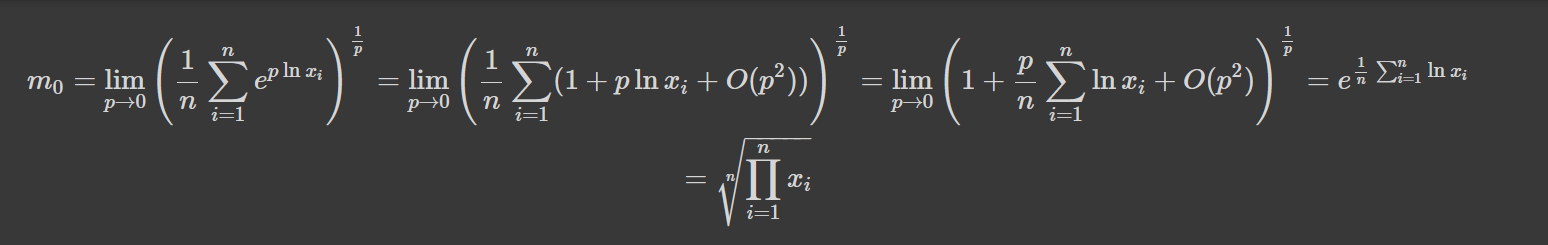
Неочікувано, ми отримуємо середнє геометричне!

Постає питання: а чи потрібні нам середні функціональні окрім середніх степеневих? Відповідь: так. Повернемось до питання про зоряну величину. Різниця зоряних величин двох об'єктів визначається як:

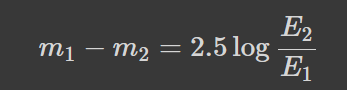
Де Е -- освітленість, яку створює об'єкт, а логарифм десятковий (я знаю, що він позначається lg, але формули лінь переписувати). Тобто чим яскравіший об'єкт, тим менша його з.в. Середня зоряна величина відповідає об'єкту, який створює вдвічі меншу освітленість, ніж дві зорі разом взяті. Наприклад, середня величина системи з дуже тьмяної (m=безкінечність) і дуже яскравої (m=-3) зір не буде рівна безкінечності -- зорі, яка фактично не світить, а натомість буде рівна -2.75. Тоді зоряну величину зоряного скупчення зір з величинами 5m та 7m можна знайти як:

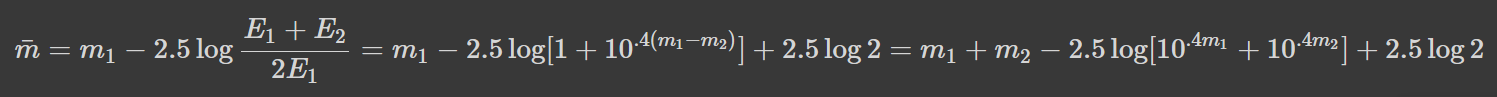
Вам може здатись, що у формули є очевидне узагальнення, але це не так. Ба більше, вона має форми квазі-арифметичного середнього. Проте один трюк все виправляє:

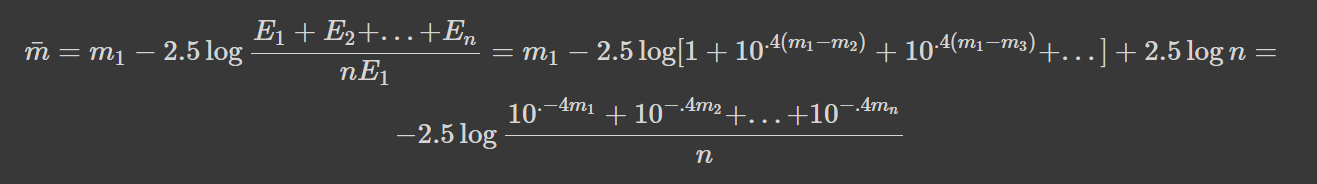
Як бачимо, тепер все добре, та й функція доволі екстравагантна. Переконаний, у вашій області зустрічаються навіть цікавіші.

То чому я програю?

Тепер до портфоліо. Ріст на 50% відповідає збільшенню в півтора рази, а скорочення на 40% -- множення на .6. Це дає загальний множний 1.5*.6=.9, що відповідає скороченню на 10%. Це, в свою чергу, приблизно рівне скороченню на 5% на рік (.9^.5-1). Яке це середнє? Геометричне, або ж фукціональне з f(x)=log(x+1).

Повернемось до задачі з монеткою. При безкінечній грі, половину разів випадатиме герб, що відповідає множнику 1.5, та іншу половину номінал -- множник .6, даючи загальний множник (внаслідок комутативності множення порядок ігор неважливий) .9^(n/2), де n -- кількість зіграних ігор. Як бачимо, при безкінечній грі ваш капітал наближається до нуля. Але що нам каже матсподівання?

Матсподівання виграшу після кожної гри, очевидно, .5*50%+.5*(-40%)=5%, тобто ви в плюсі. Знову ж таки, через лінійність і слідуючого з цього мультиплікативність матсподівання ваш середній виграш рівний 1.05^n, що рівне безкінечності при безкінечній грі. Парадокс? Чи хибна догма?

Розрахуємо ймовірність виграшу, себто виходу в плюс. Ваш виграш за n ігор є випадковою величиною, яка залежить від кількості гербів k які випали в процесі. Його розмір та ймовірність рівні (k має біноміальний розподіл):

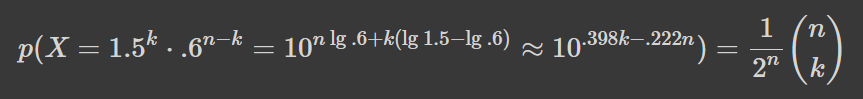
Як бачимо, можна розглядати нову змінну, лінійну: x=.398k-.222n. Для виграшу має виконуватись k>.557n, тобто кількість гербів має бути на 26% більшою за кількість номіналів. Так як за великих n та при np=n/2>30 біноміальний розподіл дуже добре апроксимується нормальним, маємо:

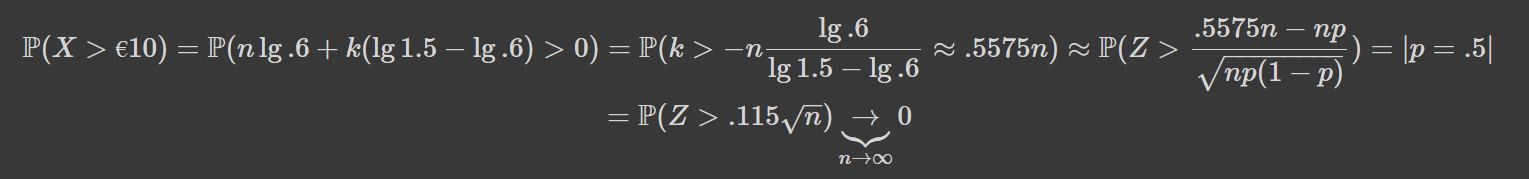
Тобто ймовірність вийти в плюс при безкінечній грі прямує до нуля. А як взагалі виглядає розподіл виграшу? Наприклад, ось так:

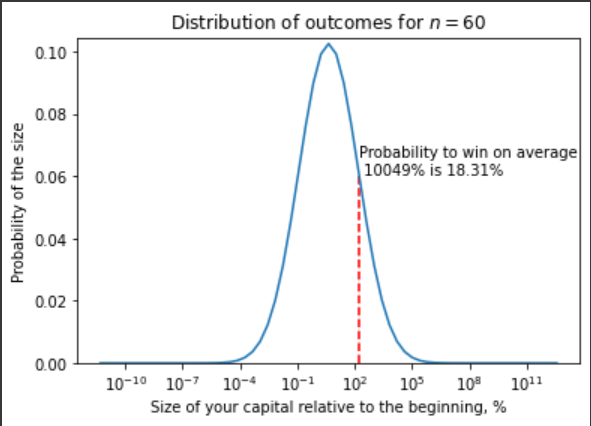
Решта мені лінь вже кодити.

Нове матсподівання

А яке ж середнє це було в першій грі? І чи не повинні ми бува переозначити матсподівання? Можна означити матсподівання функції f(X) від випадкової величини X наступним чином:

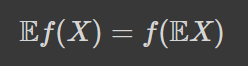
Тоді у нашому випадку воно рівне:

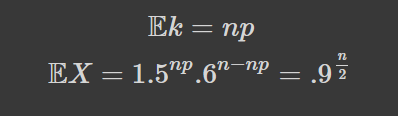
Що є куди інформативнішим у конкретно нашому випадку як матсподівання виграшу за одну гру, а не з ансамблю ігор. Чи працюватиме воно в інших випадках -- на цю тему відсилаю вас сюди за математикою і сюди за цікавим оглядом та експериментом з цією грою. Для затравки:

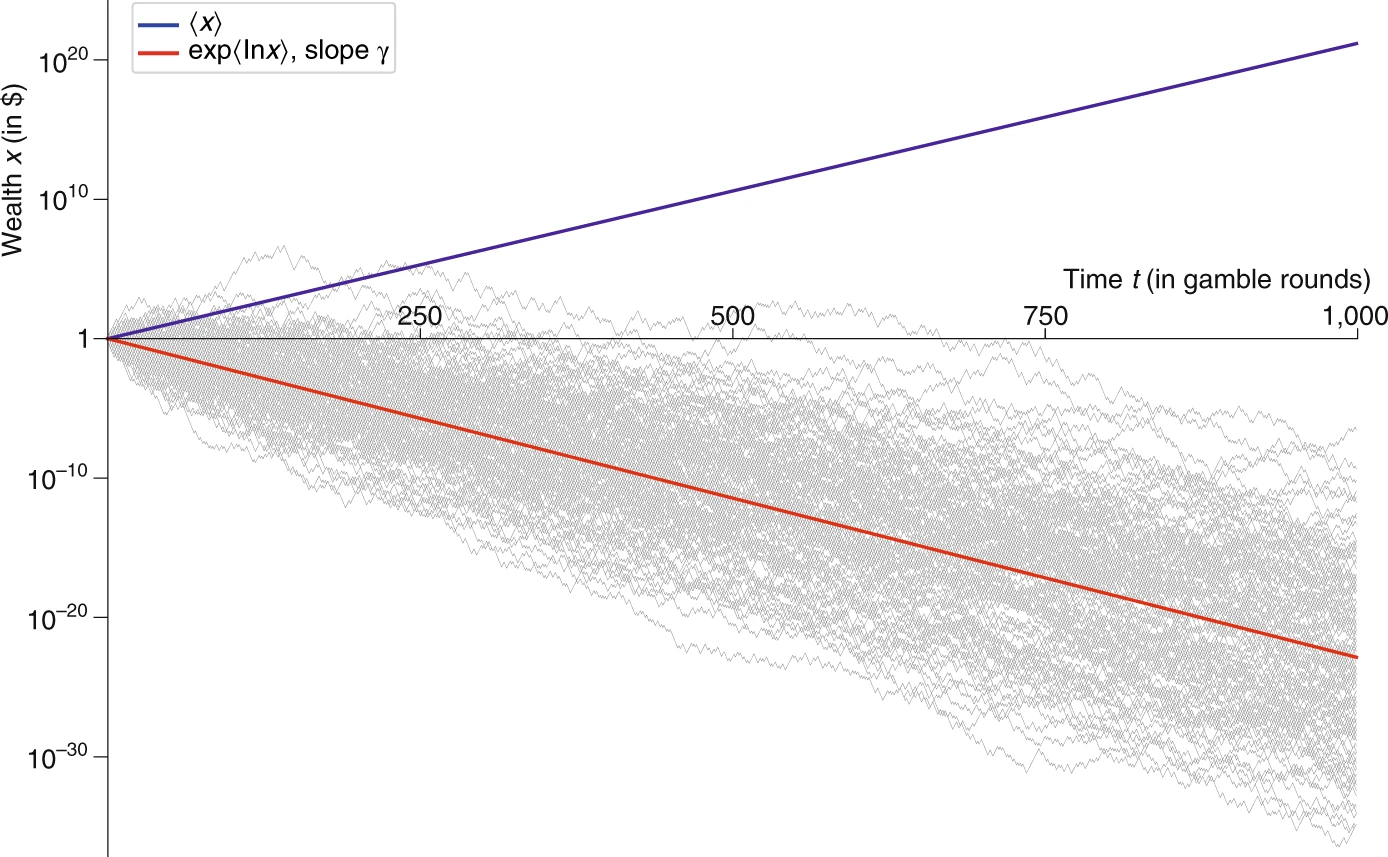
Альтернативна гра

Можна зіграти у простішу гру: з ймовірністю 1/10^9 ви виграєте мільярд гривень, у решті випадків -- втрачаєте 50 коп. Обрахуємо, яка ймовірність не виграти жодного разу під час перших двох мільйонів спроб, що вартуватиме вам мільйон гривень. Це, як легко обрахувати за допомогою другої чудової границі, рівно:

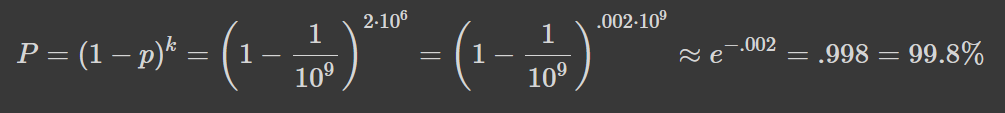
Чи готові ви витратити мільйон за .2% шанс виграти мільярд? Краще: чи готові ви купити лотерейний квиток за тисячу гривень з джекпотом на мільйон і ось таким от шансом? Ваше матсподівання знову позитивне, проте через тисячі і навіть мільйони ігор ви втрачатимете відповідно тисячі та мільйони гривень. З цього можна зробити висновок, що матсподівання не є гарним критерієм для вступання в гру: як першу, так і другу.

Чим же тоді керуватись? Здоровою виглядає ідея керуватись ймовірністю виграшу, принаймні коли кошт за вступ в гру набуває великих розмірів. Адже припустимо ви хочете відкрити стартап і знаєте, що 90% їх прогорають: 10% протягом першого року, 70% протягом 2-5 років. Матсподівання вашого багатства явно високе, проте чи встигнете ви за життя після навіть кількох спроб отримати цю цифру? Тим паче, що в Україні є суттєва ймовірність рейдерського захоплення, що робить ризики значно більш знеохочуючими. Не хочу знеохочувати вас від відкриття стартапу, але хочу, аби ви правильно обраховували ризики замість ставати жертвою систематичної помилки вцілілого.

То скільки разів треба грати в гру з монеткою?

Так як можливі виграші значно вищі за програші, грати варто стільки разів, скільки дозволить вам вигравати у половині випадків. Парна кількість для цього явно не підходить, в той час як непарна дає у найімовірнішому випадку, на рубежі між виграшами та програшами, а саме n+1 герб та n номіналів, множник .9^n*1.5, який більший за одиницю при n<4. Тож, 7 разів виглядає безпечно. Також кидки незалежні, то здавалось би, 7 разів можна грати з довільного моменту гри? Схоже на те. Я відкритий до дискусій, адже тверезо мислити тут складно, та й до того ж ця логіка змушує грати безкінечну кількість разів -- програшний варіянт. Що, в свою чергу, призводить до відмови грати навіть один раз. Може здатись, що гра фіксовану кількість разів, як от 7, це всерівно що гра один раз з множниками .9^3*1.5 та .9^4, але не забувайте і про дуже вигідні випадки, як от 5+ гербів.

Підсумки

Будьте обережні, коли звертаєтесь до середнього арифметичного без розуміння, чому потрібно використовувати саме його. Коли мова йде про мультиплікативні процеси та відсотки -- користуйтесь середнім геометричним. Пам'ятайте про кумулятивний зміст середніх, і прийде з вами сила критичного міркування.