Професійне навтікальництво

В круглому озері плаває качка. Довкола озера чатує лисиця, яка бігає вчетверо швидше ніж качка плаває. Як тільки качка досягає берега — вона миттєво взлітає і рятується від лисиці. Якщо качка починає з центру озера, то чи може вона уникнути зустрічі з лисицею? І якою мінімальною перевагою у швидкості має володіти лисиця, аби завжди могти спіймати качку?

Втікачка та переслідувачка зовсім необов'язково є дикими тваринами. На їх місці можете опинитись і ви під час купання у басейні чи ставку, як раптом хопа -- на березі опиняються непрохані гості, як от хулігани чи собаки. Впізнали? Згодні? Ба більше, середня швидкість плавця рівна близько 3.2 км/год, а бігуна -- 10.7 км/год (бігунки -- 9.3 км/год). Тож хтозна, ця задача може колись врятувати вам здоров'я чи навіть життя (dis escalated quickly). Зобразимо умову:

Спрощення та найпростіша стратегія

Лисиця пересуватиметься лише контуром озера зі швидкістю V=kv, в той час як качці доступна вся його поверхня. На думку спадає найпростіша стратегія: рвонути стрімголов до найближчої точки на березі, яка в той же час буде як найдалі від лисиці -- протилежна до неї. Так як качка починає з центру, то пройдена нею відстань буде рівна R, а отже час на добирання туди t=R/v. Лисиці ж вистачить T=πR/V=πt/k<t аби добігти туди. Тож, будучи вчетверо швидшою вона не дасть їй допливти до цієї точки. Як, до речі, не дасть і посередній бігун посередньому плавцю, а собака й поготів (24-32 км/год).

На цьому моменті ви могли б сказати "качці начхати, вона собі посидить у озері, рибки поїсть", але ж ми любимо математику (не впізнали?), тож Tatakae!

Чи можемо ми краще? Використання симетрій та лисячий вальс.

Один з прийомів розв'язання задач зветься використання симетрії. Задачі часто прохають про знаходження певних оптимумів, а як ви могли помічати, за наявності симетрій оптимуми часто перебувають у місцях, які симетричні самі собі: як от у парної функції в точці x=0 завжди буде максимум або мінімум.

У випадку нашої геометричної задачі, ми вперше використали симетрію для втечі у протилежну від лисиці точку: вона була найвіддаленішою від лисиці, бо в обидва боки давала однакове значення відстані. Обрали б ми довільну іншу точку, лисиця просто обрала б коротший шлях і фініта. Якщо позначити точки на колі за кутами від 0 до 2π, то відстань від лисиці в точці 0 до точки х рівна min(x,2π-x). Легко переконатись, що максимум цієї функції знаходиться в точці x=π -- точці симетрії, в якій обидва аргументи функції рівні.

Це також ефективний метод розв'язку головоломок на кшталт знайомої для вас:

Можна помітити, в задачі є симетрія між яблуками та апельсинами -- поміняй їх місцями, і умова не зміниться. Метод підказує, що увагу варто звернути на мішок з симетричною відносно двох фруктів наліпкою, і справді -- витягування звідти дасть точну відповідь на питання, який саме фрукт знаходиться в ньому. В той же час, брання яблук з мішка з наліпкою, що відповідає одному фрукту, не є інформативним, бо випадок витягання звідти іншого фрукту означатиме, що там або мікс, або інший фрукт.

Тепер домашнє завдання: уявіть перегони між командами з двох хлопців. У кожної команди є одномісний велосипед, який не витримує двох людей. Якщо швидкість бігу хлопців 10 км/год, а їзди -- 20 км/год, то за який мінімальний час команда може подолати дистанцію у 20 км? Себто, коли найшвидше обидвоє членів команди досягнуть фінішу?

Порушення симетрії

Проте симетрії можна не лише слідувати, а й ламати, порушувати. Розгляньте наступну задачу, розв'язок якої я зараз не наводитиму (тож можете спокійно читати статтю далі), зате надав підказку в пості на каналі (під спойлером):

У нашій задачі ми не лише послідували симетрії, але й змушені були її порушити задля досягнення успіху -- покинути комфортну рівновіддалену точку огляду озера. Аби досягти кращого результату, ми маємо вчинити це знову -- витурлити качку з центру, що змусить лисицю бігти до найближчої до качки точки. Таким чином, ми порушуємо не лише центральну (обертальну) симетрію, але й симетрію осьову -- лисиця тепер знає, куди їй бігти.

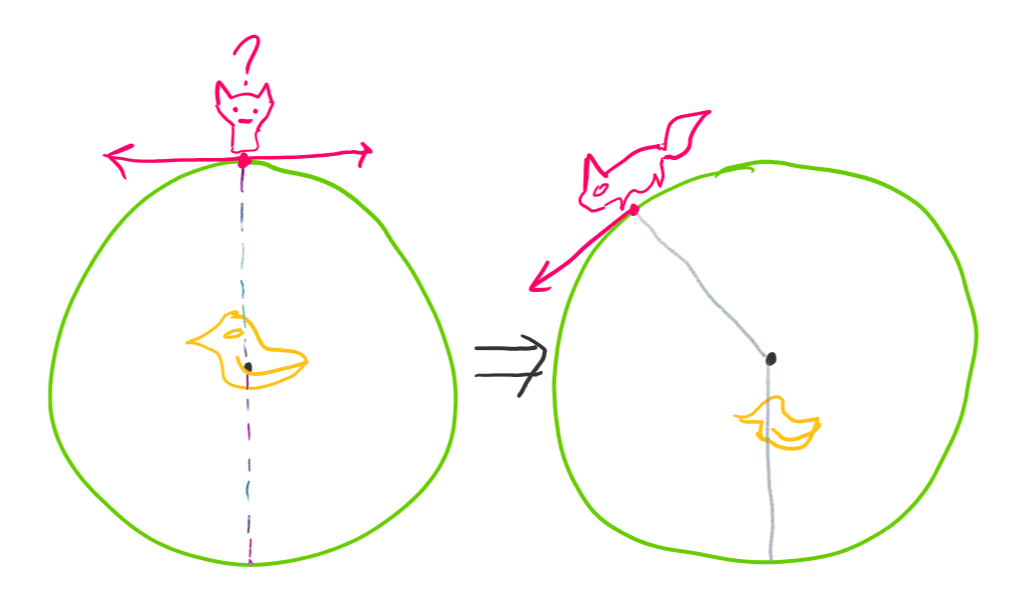
Хороші новини полягають у тому, що одну з цих двох симетрій, а саме осьову, ми здатні відновити. Адже в наших силах не лише наблизитись до берега, але й віддалити лисицю від точки, якої ми прагнемо. Чи можемо ми звести ситуацію до наведеної нижче?

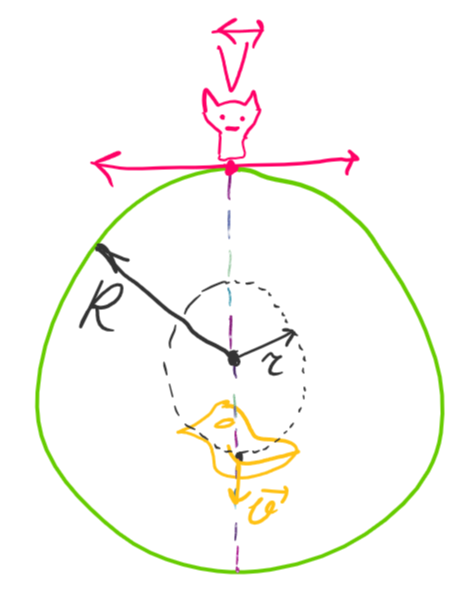
Так! Пригадуєте щось про обертання?

Вологий вальс (тобто не качиний)

Сконцентруємося на досягнення вищенаведеної позиції. Як тільки качка лишить центр, лисиця стрілою попрямує в один з двох боків, і зробить кут між собою та найближчою до качки береговою точкою менше за п. Нехай тепер качка кружлятиме довкола центру на певній відстані r. Її кутова швидкість рівна v/r, в той час як кутова швидкість лисиці V/R. Як бачимо, яка б не була велика швидкість лисиці, качка знайде як завгодно малий радіус кружляння r, аби мати більшу кутову швидкість і завдяки цьому вийти на пряму лисиця-центр. Це коло спротиву має найбільший, граничний радіус кружляння рівний r=vR/V=R/k -- з рівності кутових швидкостей. У випадку k=4 це дозволяє скоротити відстань до точки втечі на чверть, а отже новий час втечі рівний (R-R/k)/v=(k-1)/π*T=3/π*T<T -- качка встигає вислизнути! Відповідь на перше питання задачі -- так.

Оптимізація

Тепер до питання найменшої переваги лисиці. За якого найменшого k вона завжди зможе піймати качку, незалежно від стратегії останньої? Себто, за найкращої стратегії пернатої.

Наївна оптимізація

Візьмемо вираз для часу втечі згори і побачимо, що він дає t=T при k=π+1~4.14. Чи означає це, що за k>4.14 лисиця не дасть качці досягнути берега і здобути волю? Ні. Ба більше, успіх лисиці не гарантований навіть при k=4.5.

Базована оптимізація

Пам'ятаємо про головне: мета качки досягти берега раніше за лисицю. І тому хоч качка і має швидкість меншу за лисячу, а після виходу з кругу спротиву і кутова швидкість качки буде меншою, у качки в запасі є відстань до хижачки. А як ми знаємо з попередньої статті, перевага у швидкості не завжди означає успіх у полюванні.

Підемо схожим шляхом: порушимо останню симетрію, яка в нас лишилась. Після досягнення відстані r=R/k від центру і вальсування з лисицею качка вже не зможе кружляти так, щоб тримати кут рівним π, тому лишається лише рванути до берега. Далі виконуються наступні твердження:

1) Її оптимальна траєкторія наразі може мати довільну форму -- проте вона точно не перетинатиме круг спротиву, бо це поверне нас до початку оптимізації -- його полишання.

2) Відстань качки до центру повинна монотонно (з часом) збільшуватись, інакше вона лише дасть фору лисиці.

3) Як тільки лисиця визначилась, в який бік бігти -- ми кренимось у протилежний (як на рисунку):

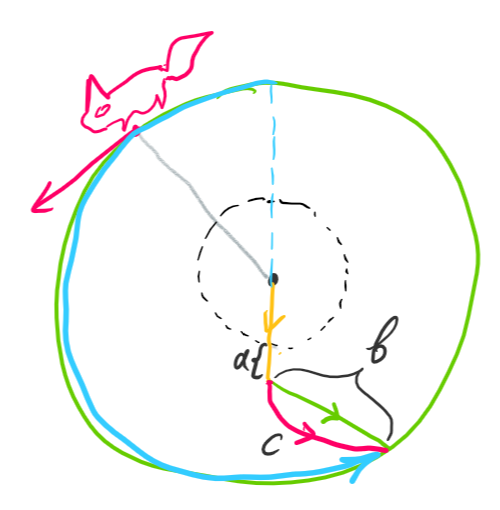
Зазначимо, що як тільки лисиця визначилась з напрямком руху, змінювати його для неї неоптимально -- кут між нею та качкою у обраному напрямку завжди буде меншим за π внаслідок постійної переваги у кутовій швидкості. (Якщо ж качка здуру захоче назад у круг -- лисиця змінить напрям руху, і гонка почнеться спочатку.) Це, в свою чергу, дозволяє зробити нам відрізок a як завгодно малим. Тепер, так як траєкторії b та c ведуть в одну точку, і рух по них відбувається з однаковою сталою швидкістю, траєкторія b буде оптимальніша по часу, бо це пряма лінія. Аналогічно, подорож по a+b в одну й ту саму точку буде мінімальна якщо а матиме довжину 0 -- з нерівності трикутника. Це приводить до фінального твердження:

4) Оптимальна траєкторія починається з кола спротиву і є відрізком.

Професійна оптимізація (без складної математики)

Наша задача тепер виглядає так:

Наразі ми намагаємось уникати математики якомога сильніше, тому перше рівняння не потребує значної уваги. Натомість, споглядаючи рисунок можемо помітити, що рух лисиці по великому колу (озера) еквівалентний руху меншої лисиці-плавця по малому (колу спротиву) з такою ж кутовою швидкістю, а отже з лінійною швидкістю качки! Тобто рівність тривалостей руху по траєкторіях еквівалентна рівності довжини дуги малого кола та відрізку l. У навтікальницьких інтересах качки збільшити цю дугу, не збільшуючи свій шлях l настільки ж сильно. Чи дає нам це щось? Несильно.

Припустимо, качка обрала певну точку С, до якої пливтиме з точки В, яка знаходиться на колі спротиву (рис. нижче). Вирахуємо, скільки додасться до шляхів качки та лисиці, якщо ми натомість оберемо точку D, яка дуже близько до С. Маємо перший крок (x<<1 означає, що кут x дуже малий, значно менший за 1 рад):

Після наближення дуги відрізком перейдемо до розгляду трикутника BCD, і з нього вирахуємо різницю у шляхах качки:

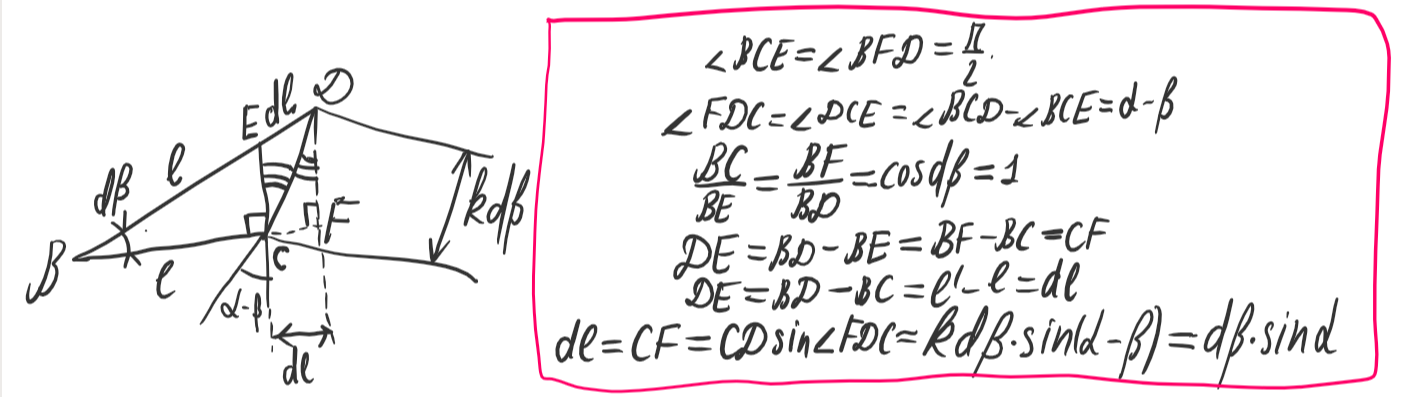
Різниця у шляхах лисиці вираховується дуже просто -- пропорційна до кута dß. З умови того, що збільшення часу на подорож качки має бути менше, ніж у лисиці, аби зміна траєкторії мала сенс, маємо:

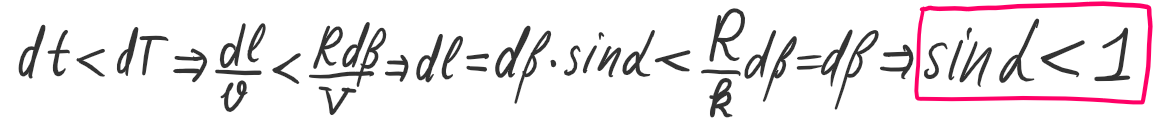
Як бачимо, при зміщенні точки втечі С проти годинникової стрілки ми виграємо час у порівнянні з лисицею при всіх кутах крену альфа окрім одного -- прямого, π/2. Саме коли кут альфа прямий, зміщення вгору не змінює ситуації. Аналогічно, при зміщенні точки С за годинниковою стрілкою, або ж вниз, час подолання шляху у лисиці зменшується на більшу кількість секунд, ніж у качки, тому це вигідно для лисиці -- проте не тоді, коли альфа рівне прямому куту. Тож, стратегія найвірнішої втечі за довільного k виглядає ось так:

Де всередині кола спротиву зображено ймовірне вальсування качки проти лисиці до виходу на пряму лисиця-центр. Вальсування самої лисиці лишається як вправа читачу.

Цього, до речі, можна було очікувати, якби ми могли прийти очевидніше до того факту, що зсовувати точку втечі вбік вигідно. Або ж якби ми знали, що рухатись в той чи інший бік вигідно для всіх точок, нам лишалось би обрати між протилежною та перпендикулярною -- це єдині точки, від яких можна рухатись лише в один бік з двох. Зазвичай, екстремуми можуть знаходитись не лише всередині, але й на краях області визначення, бо саме там похідна часто не береться зовсім.

Знаходження мінімального k

Останнє, тобто досі друге, питання, на яке ми маємо відповісти, криється в максимальному значенні k, за якого такі викрутаси можливі -- себто траєкторія. Якщо k=π+1, то цілитись можна в довільну точку -- втеча гарантована. При все більшому k область берега, в яку можна втікати, все вужчатиме. Це наочно зображено в цьому GeoGebra аплеті, можете погратись (рухомими є повзунки та Точка втечі).

Очевидно, що при максимальному k ця область стиснеться в одну точку -- перпендикулярну до початкової прямої лисиця-качка. В аплеті можна побачити, що цей максимум рівний близько k=4.60. За більших значень лисиця завжди спіймає качку (або собаки вас на виході з озера). Чому рівне точне значення k? Тут вже без щонайменше калькулятора не обійтись, бо потрібно розв'язати наступне рівняння:

де зліва це шлях качки з теореми Пітагора, а справа -- шлях лисиці-плавця з означення косинусу.

Професійна оптимізація (з матаном)

Забудемо все вищесказане після твердження 4. Нехай при певному k оптимальній траєкторії відповідає центральний кут ß. З теореми косинусів запишемо умову рівності часів подолання шляхів:

Так як ми шукаємо максимальне k, за якого це рівняння має розв'язок, продиференціюємо обидві його частини по ß і прирівняємо похідну k' до нуля:

Отримали рівняння, схожі на виведені геометрично. Дійсно, l=k sin ß лише за умови, що l є протилежним катетом до гіпотенузи довжиною k -- отримуємо перпендикулярність траєкторії качки. Після нескладної алгебри отримуємо рівняння на максимальне k, але записане через оптимальний ß та в два кроки:

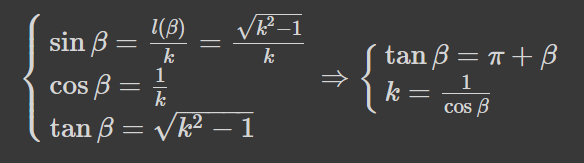
Чисельний розв'язок якого вимагає методів, складніших за f(f(f(...f(x)...)=x, та дає x=4.60334...

Шляхом матану ми уникли купи слів та рисунків, натомість швидко прибули до відповіді. В цьому частково і є одна з моралей Манга-Путівника до Числення:

Підсумки та домашнє

Ми розв'язали задачу з купою симетрій, експлуатуючи їх та ламаючи, навчаючись ними послуговуватись у всі можливі способи. Брешу, ми просто розв'язали одну задачу: зате без матану, певно вперше в історії каналу.

Оптимальною траєкторією виявилась пряма лінія. Можна, до речі, показати (у відео помилка щодо максимального k), що тактики на кшталт "рухатись по прямій від кота" та "рухатись назустріч точці, протилежній від кота", не спрацюють. Ми це знаємо з попередньої статті, бо ці тактики намагаються звести відносну швидкість до нуля, забуваючи про мету -- втекти, що тут визначається відстанню.

Автору варто було б теж не займатись речами, які буцімто тримають відстань від зовнішніх загроз у лиці обов'язків скінченною, а натомість ведуть до його кінця. Навпаки, потрібно набратись хоробрості, відваги, раціональності, і всього, що є антитезою до хаосу, і зустрітись з лисицею на її території, після чого здійнятись у небо з розпростертими крилами.

Для складнішого домашнього завдання можна помислити над наступною загадкою: