Хеш-кодирование
Алексей Тарасов @AtarВводная
1. Однослойная сеть из хеш-нейронов кодирует произвольный бинарный вектор в распределённое бинарное представление (бин. вектор) близкой к постоянной плотности — хеш.
2. Мы можем оценивать схожесть образов, закодированных в признаковом пространстве, путём вычисления степени корреляции их хешей.
Примеры кодирования
Входным образом будем называть входной бинарный вектор.
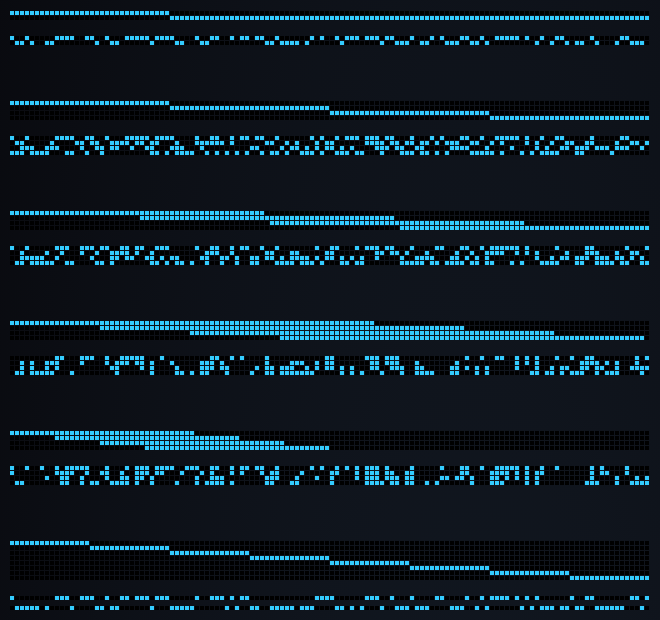
1) Для начала рассмотрим произвольный образ и его инверсию.
В верхних двух строках два входных образа: целевой образ и инверсный. Ниже выведены их хеши.
Как видно, от векторов с сильно различающейся плотностью получены хеши с близкой плотностью и равномерным распределением.
Пересечение единичных бит в хешах не наблюдается. Значение корреляции между ними, соответственно, равно 0.
2) Далее представлены четыре входных образа без общих признаков. Как видно, теперь их хеши пересекаются друг с другом.
Плотности хешей [0.43, 0.46, 0.46, 0.46]
В таблице дана матрица корреляции этих хешей друг с другом.
| | 0.15 | 0.14 | 0.15| |0.15 | | 0.17 | 0.15| |0.14 | 0.17 | | 0.16| |0.15 | 0.15 | 0.16 | |
3) Теперь возьмём на 50% пересекающиеся "соседние" образы.
Плотности хешей практически не изменились: [0.41, 0.43, 0.44, 0.43]. Изменилась корреляция хешей друг с другом.
| | 0.20 | 0.07 | 0.07| |0.20 | | 0.22 | 0.08| |0.07 | 0.22 | | 0.22| |0.07 | 0.08 | 0.22 | |
Мы задали, что первый образ имеет 50% пересечение со вторым и не имеет общих признаков с третьим и четвёртым.
Второй образ имеет пересечение как с первым так и с третьим образом и не имеет пересечений с четвёртым.
Вся эта информация отношения образов друг с другом отразилась в связности хешей. По таблице видно как изменились их корреляции. У схожих образов корреляция в их хешах увеличилась, а у не пересекающихся — уменьшилась.
4) Cлучай сильного перекрытия входных образов.
Плотности хешей немного просела: [0.36, 0.36, 0.36, 0.36]. Это вызвано тем, что плотность входных образов поднялась выше 0.5, а "плоскость" плотности генерируемого хеша не идеальна и падает для высокой входной плотности.
| | 0.20 | 0.11 | 0.02| |0.20 | | 0.20 | 0.11| |0.11 | 0.20 | | 0.20| |0.02 | 0.11 | 0.20 | |
В таблице мы видим сохранение высокой связности с соседним образом и почти полную ортогональность с дальним, но всё же имеющим пересечение.
Если посмотреть на первый и четвёртый образы, то суммарно они захватили всё входное пространство, но друг с другом имеют небольшое пересечение. Этим и вызвана ортогональность их хешей. Они, скорее, непохожи, чем похожи.
5) Мы можем "усилить" корреляцию хешей простым "масштабированием" входных образов.
Плотности хешей [0.42, 0.41, 0.41, 0.41]
| | 0.29 | 0.23 | 0.17| |0.29 | | 0.29 | 0.22| |0.23 | 0.29 | | 0.29| |0.17 | 0.22 | 0.29 | |
Корреляция хешей по схожести образов друг с другом теперь близка к линейной. Она отражает ту взаимосвязь образов, которую мы и закладывали.
На практике такую технику я применяю в следующих случаях.
Например, требуется сгенерировать коды для монотонно возрастающей/убывающей последовательности "сущностей". Это может быть ряд позиций (буквы в слове): 1, 2,... 9, где необходимо в коды заложить корреляцию, отражающую идею пространства — рядом с позицией 1 есть позиция 2, а самой дальней должна быть позиция 9.
Аналогично можно закодировать цвета в радуге. То есть, сохранить информацию о последовательности цветов.
6) И ещё пример — кодирование набора стимулов.
Восемь непересекающихся входных образов. Например, это может соответствовать буквам: A, B, C, D, E, F, G, H. И мы кодируем ими два слова ABCD и EFGH. Для этого берём хеш от объединения (лог. OR) образов, составляющих слово. Корреляции хеша слова ABCD с хешами каждой буквы следующие:
|0.23 | 0.24 | 0.23 | 0.25 | 0.11 | 0.13 | 0.11 | 0.12|
Видно, что хеши букв (E, F, G, H), которые не входят в слово ABCD, имеют вдвое меньшую корреляцию с хешем слова ABCD, чем хеши букв A, B, C, D.
Так же на рисунке видна высокая ортогональность хешей слов (последние две строчки), так как они составлены из непересекающихся наборов букв (аналог первого примера). У близких же по набору составляющих их букв слов, вроде МАША и КАША, будут близки и их хеши. И тем больше, чем больше общих букв в сравниваемых словах.
Итог. Можно получить корреляцию хешей отражающую изначально такую имеющуюся у кодируемых ими объектов.