Мультипликативный корреляционный нейрон

Sparse Hash

На идею о том, что у нейрона может быть такая вычислительная функция, меня навёл пост на Хабре Александра Ершова @Ustas об оригинальном способе перемножения вещественных чисел.

Этот метод перемножения работает с числами из диапазона [0, 1]. Значения величин кодируются в бинарные последовательности со стохастически равномерно распределёнными единичными значениями. "Погонная" плотность единиц равна значению величины. Например, значение 0,5 кодируется в последовательность с примерно равным количеством единиц и нулей.

Важное значение имеет то, что единицы должны быть распределены равномерно по последовательности.

При побитном логическом сложении (AND) таких последовательностей фактически происходит операция умножения. Плотность единиц результирующей последовательности равна результату умножения входных величин.

Точность задаётся длиной стохастической бинарной последовательности. Исходник простого примера, демонстрирующего алгоритм.

Пример

Длина последовательностей равна 100. Плотность выходной последовательности соответствует произведению 0,7 * 0,4 = 0.28.

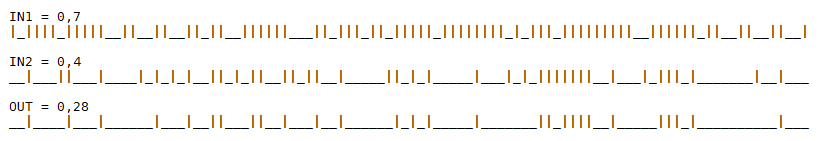
Давайте далее вместо последовательности будем рассматривать аналогичный бинарный вектор. Тогда операция сложения будет происходить не побитово, а сразу над всем вектором. Операцию умножения в таком случае можно выразить простой формулой: countOnes(a & b) / a.length.

Теперь один входной вектор примем за текущую входную активность нейрона. А второй вектор будет синаптической картой выходного нейрона.

Единичным значениям в векторах соответствуют сработавший входной нейрон и наличие синапса с этим входным нейроном соответственно.

Все синапсы возбуждающие и имеют постоянный вес. Примем для удобства его за единицу. Передаточная функция нейрона - сумматор. Как видно из примера ниже, выходное значение нейрона (0.28) равно произведению входной активности (0.7) на синаптическую карту (0.4). То есть, нейрон работает как умножитель.

Какое всё это имеет отношение к нейронным кластерам? Делаю предположение, что такой нейрон-мультипликатор в мушиной схеме отвечает за формирование кластеров. Фактически кластер из хеш-нейронов отображается в синаптическую карту нейрона-мультипликатора. Нервная система мухи способна сформировать столько самообучаемых классификаторов, сколько у неё таких нейронов.

Вся ранее описанная схема формирования кластеров остаётся без изменений. Меняется только формула расчёта близости векторов на новую.

На практике нейрон-мультипликатор показал себя превосходно, уровень выхода годных/сформированных кластеров поднялся к 99%. И главное, появилось объяснение почему вся эта схема на кластерах из хеш-нейронов вообще работает. Ответ простой - кластер, или его отображение в виде мультипликативного нейрона, находят корреляцию между входным образом и своим внутренним. Поэтому нейрон-мультипликатор можно назвать ещё и корреляционным.

Равномерность заполнения и длина вектора играют определяющую роль. Хеш нейроны создают хеши (активность слоя) постоянной плотности равной разреженности выхода хеш-нейрона. Допустим разреженность равна 0,5. Тогда два случайных образа отобразятся в два хеша/вектора с плотностью единиц равной 0,5. Их произведение будет равно вектору с плотностью 0,25. То есть, значение 0,25 соответствует отсутствию корреляции между образами.

У близких же образов хеши также будут близкие (по Хеммингу). Обратите внимание, что плотность хешей близких образов остаётся такой же как и у несхожих образов. У близких образов в хешах наблюдается корреляция в их битах (единичных значениях), что нарушает требование равномерности заполнения для правильного перемножения. В итоге у близких образов произведение хешей происходит с ошибкой, величина отклоняется, и тем больше, чем больше совпадение в хешах.

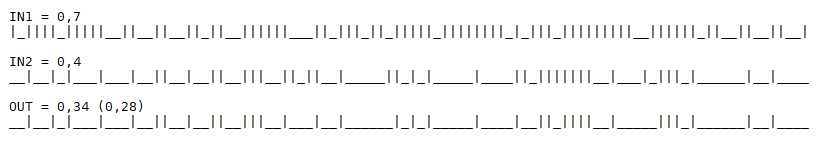
В итоге, активность кластера - это величина, отражающая корреляцию между входным образом и образом, хранимым этим кластером.

И ещё, корреляционный (или кластерный) нейрон у мухи имеет множество обратных связей, через которые он тормозит хеш-нейроны. В моей модели колонки коры это необходимо для формирования выходного кода колонки. Победивший кластерный нейрон тормозит все хеш-нейроны за исключением тех, которые соответствуют его хранимому образу.