maximum-value-of-k-coins-from-piles

There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.

Example 1:

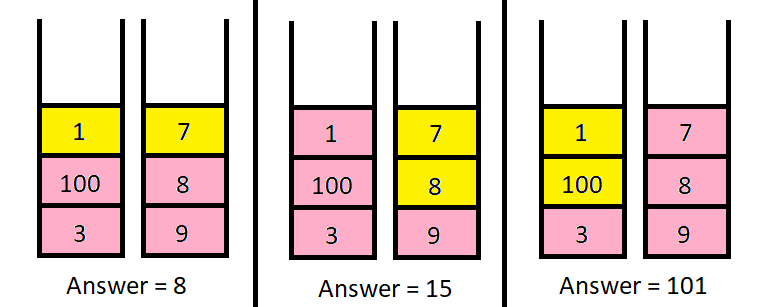
Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Example 2:

Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

Constraints:

• n == piles.length


• 1 <= n <= 1000


• 1 <= piles[i][j] <= 105


• 1 <= k <= sum(piles[i].length) <= 2000