find-the-number-of-ways-to-place-people-i

给你一个  n x 2 的二维数组 points ，它表示二维平面上的一些点坐标，其中 points[i] = [xi, yi] 。

计算点对 (A, B) 的数量，其中

• A 在 B 的左上角，并且


• 它们形成的长方形中（或直线上）没有其它点（包括边界）。

返回数量。

示例 1：

输入：points = [[1,1],[2,2],[3,3]]

输出：0

解释：

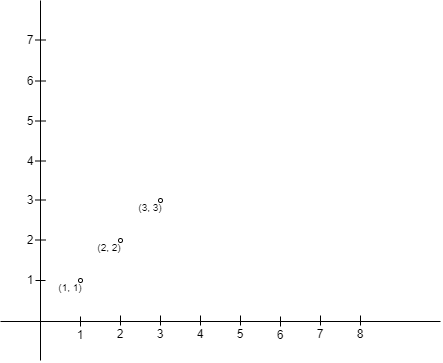
没有办法选择 A 和 B，使得 A 在 B 的左上角。

示例 2：

输入：points = [[6,2],[4,4],[2,6]]

输出：2

解释：

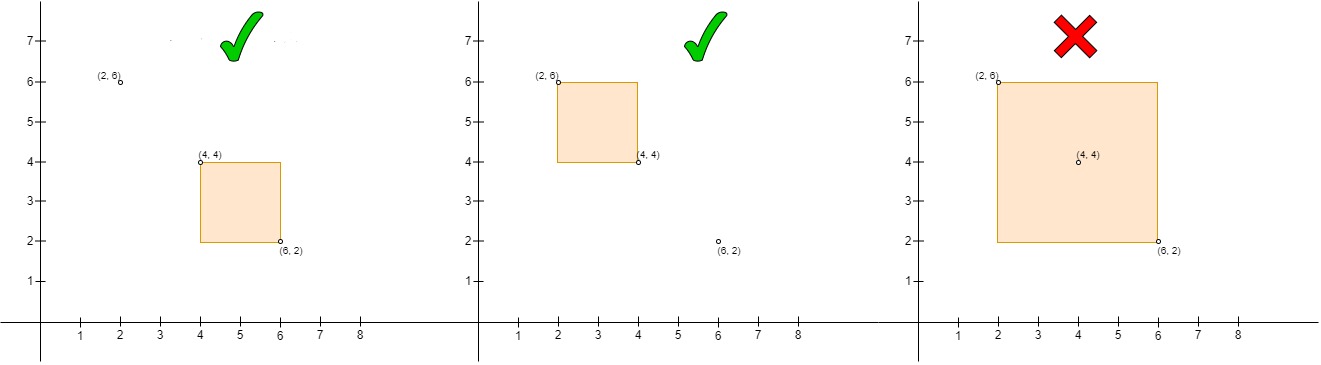
• 左边的是点对 (points[1], points[0])，其中 points[1] 在 points[0] 的左上角，并且形成的长方形内部是空的。


• 中间的是点对 (points[2], points[1])，和左边的一样是合法的点对。


• 右边的是点对 (points[2], points[0])，其中 points[2] 在 points[0] 的左上角，但 points[1] 在长方形内部，所以不是一个合法的点对。

示例 3：

输入：points = [[3,1],[1,3],[1,1]]

输出：2

解释：

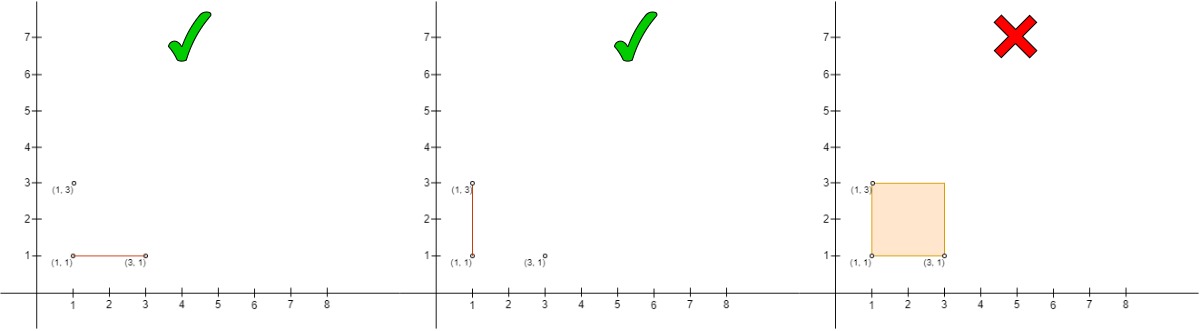
• 左边的是点对 (points[2], points[0])，其中 points[2] 在 points[0] 的左上角并且在它们形成的直线上没有其它点。注意两个点形成一条线的情况是合法的。


• 中间的是点对 (points[1], points[2])，和左边一样也是合法的点对。


• 右边的是点对 (points[1], points[0])，它不是合法的点对，因为 points[2] 在长方形的边上。

提示：

• 2 <= n <= 50


• points[i].length == 2


• 0 <= points[i][0], points[i][1] <= 50


• points[i] 点对两两不同。