count-the-number-of-complete-components

You are given an integer n. There is an undirected graph with n vertices, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting vertices ai and bi.

Return the number of complete connected components of the graph.

A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.

A connected component is said to be complete if there exists an edge between every pair of its vertices.

Example 1:

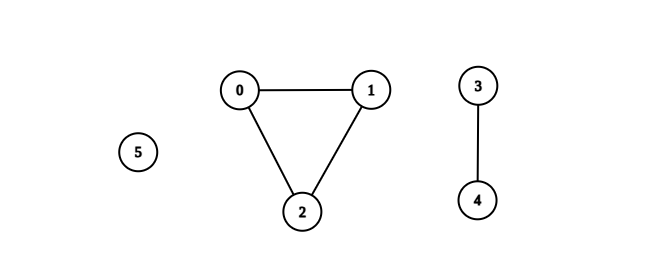
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
Output: 3
Explanation: From the picture above, one can see that all of the components of this graph are complete.

Example 2:

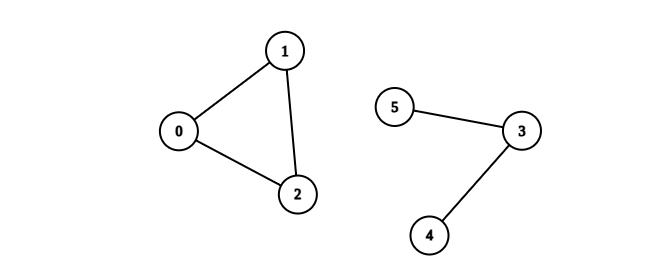
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
Output: 1
Explanation: The component containing vertices 0, 1, and 2 is complete since there is an edge between every pair of two vertices. On the other hand, the component containing vertices 3, 4, and 5 is not complete since there is no edge between vertices 4 and 5. Thus, the number of complete components in this graph is 1.

Constraints:

• 1 <= n <= 50


• 0 <= edges.length <= n * (n - 1) / 2


• edges[i].length == 2


• 0 <= ai, bi <= n - 1


• ai != bi


• There are no repeated edges.