Машиннообучаемые потенциалы и дальнодействие в задачах исследования материалов

Краткий разбор статьи: Machine learning interatomic potentials and long-range physics, DOI: https://doi.org/10.1021/acs.jpca.2c06778

September 06, 2024

Несмотря на то, что машиннообучаемые потенциалы — мощный инструмент для моделирования  систем, включающих тысячи атомов, с ab initio точностью, у него все еще есть ограничения в применении. Например, воспроизведение электростатических, Ван-дер-Ваальсовых (ВдВ), индукционных и других нековалентных взаимодействий до сих пор является задачей, решенной лишь частично.

Один из недавних обзоров на эту тему описывает современные подходы как к общепризнанным методам учета Кулоновского взаимодействия (например, charge equilibration (Qeq)), так и к их альтернативе — учету дальнодействующих взаимодействий через message passing, а также обозначает общие черты и различия в подходах по учету ВдВ взаимодействий.

Изначально, проблема учета дальнодействующих взаимодействий происходит из приближения локальности, использующегося во всех современных машиннообучаемых потенциалах, и позволяющего аппроксимировать полную энергию в виде разложения по вкладам энергий отдельных атомов в их локальных окружениях,

где энергия атома E_i определяется взаимодействием только с теми его соседями, которые попадают внутрь некоторого радиуса отсечки (обрезания) R_cut. При том, что для сохранения времени вычислений в приемлемом диапазоне и ограничения числа взаимодействующих соседей, обычно используется радиус отсечки от 5 до 7 Å, в то время как ВдВ взаимодействия затухают только на расстоянии около 10 Å, а Кулоновские — на расстояниях более 20 Å.

Авторы предлагают рассматривать любой машиннообучаемый потенциал, учитывающий дальнодействующие взаимодействия, как относящийся к одной из трех категорий: 1) пренебрегающий ими; 2) описывающий их с помощью стандартной для данного взаимодействия функциональной формы (например, кулоновским потенциалом или дисперсионной поправкой, использующейся в DFT), параметры которой (например, заряды) зависят только от локального окружения; 3) учитывающий зависимость параметров дальнодействующего потенциала от атомов вне локального окружения.

Для учета Кулоновского взаимодействия используются потенциалы и типа 2, и типа 3. В обоих случаях к энергии локального потенциала добавляется вклад, зависящий от зарядов на атомах.

У этого подхода есть много вариаций, поскольку, можно дополнительно учесть как влияние на заряд атомов вне локального окружения, так и отойти от аппроксимации зарядов как точечных, что позволяет моделировать поляризацию. Также, поскольку заряд атома не является наблюдаемой величиной,  его можно как присваивать на основе одного из методов распределения зарядов (charge partitioning), так и делать машиннообучаемым параметром.

Для демонстрации различия между локальным потенциалом (тип 1) и потенциалом, учитывающим электростатическое взаимодействие (типы 2 и 3) авторы приводят работу, сделанную для димеров заряженных или полярных молекул.

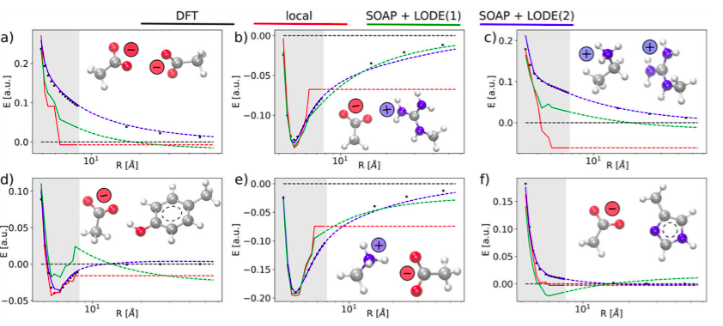
В то время как различие между потенциалами типов 2 и 3 подробно описано и продемонстрировано на примерах в другой работе. Например, только потенциал 3 типа, учитывающий влияние нелокальных эффектов на заряды, способен предсказать перераспределение заряда в системе с сопряженными π-связями после протонирования.

Для учета ВдВ взаимодействий, большинство подходов предполагают, что отталкивающая часть потенциала может быть “выучена” локальным машиннообучаемым потенциалам, тогда как дополнительно нужно получить только притягивающую часть. Для ее моделирования популярны дисперсионные поправки, использующиеся в DFT (от D2 до MBD), где часть параметров делается машиннообучаемой.

Такие подходы были успешно применены для создания машиннообучаемого потенциала для нескольких фаз углерода, включая жидкость, фуллерены и графен, а также потенциала, описывающего несколько фаз фосфора, включая жидкость и фосфорен.

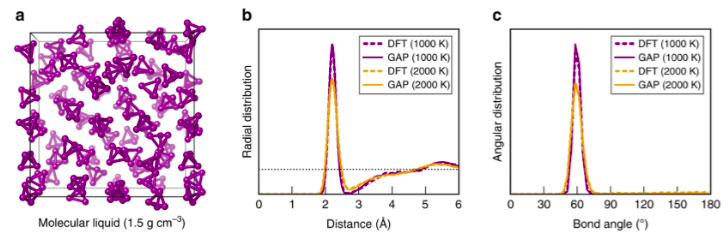
В то же время, выбор конкретного типа потенциала должен мотивироваться исследуемой системой: даже полярные системы, где заряды хорошо экранированы (например, некоторые из жидких электролитов), можно моделировать локальным потенциалом, а потенциалы типов 2 и 3 будут избыточными. Тогда как для таких систем как двумерные материалы, или системы с водородными связями, использование моделей типов 2 и 3 необходимо.

Однако, не дизайн машиннообучаемого потенциала, учитывающего дальнодействие, а набор конфигураций для его обучения сейчас рассматривается как бутылочное горлышко для применения этих методов. Решение этой задачи лежит в применении методов активного обучения, большинство из которых все еще остаются вычислительно дорогими, и кроме того все еще не способны достаточно широко охватывать интересующую часть конфигурационного пространства.