Задача из молодости

Когда-то на первом курсе (уже 5 лет назад, ого!) мне показали очередную задачу на codeforces. Я её довольно сильно запомнил, потому что она не очень сложная с точки зрения математических рассуждений и красиво сворачивается в понятный ответ (который ещё и считать несложно, но чуть сложнее базовых операций).

Надо уточнить, что я в целом не поклонник математических задач на контестах по спортивному программированию. Надо скорее на силу рук, писать сложные конструкции. Проверять продвинутый навык код писать, а не формулы выводить.

Собственно задача:

Контест: Helvetic Coding Contest 2016. Ссылочка на задачу: https://codeforces.com/contest/690/problem/D2. Вы можете найти разбор задачи самостоятельно, но я расскажу подробнее.

Давайте формализуем.

Все кирпичи неотличимы. Т.е. если мы хотим положить t кирпичей в колонну, то мы можем сделать это одним единственным способом. x_i -- кол-во кирпичей в i-й колонне. x_pile -- кол-во кирпичей, которые не были использованы для строительства стены. Теперь можем зафиксировать условия:

• Каждая колонна содержить неотрицательное количество кирпичей:

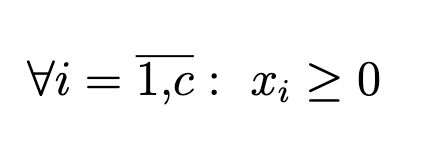
• Все колонны суммарно содержат как минимум один кирпич:

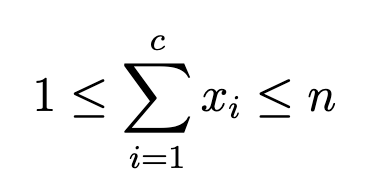
• Количество использованных и неиспользованных кирпичей равно n:

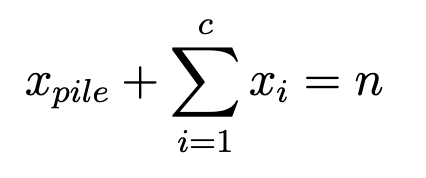
• Из условий выше:

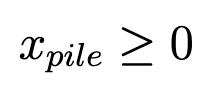
Можем свести эту задачу к более простой. Зафиксируем m кирпичей и попытаемся понять, сколько стен мы можем построить из них. Это очевидно задача разбиения числа на с слагаемых, при этом порядок слагаемых имеет значение (т.к. получаются очевидно разные стены!) и они могут быть нулевыми. Предположим, что последнего условия про нулевые слагаемые нет. Т.е. мы хотим, чтобы x_i ≥ 1. Сколько существует способов разбить число m на слагаемые при таких условиях?

Пусть у нас есть m единичек:

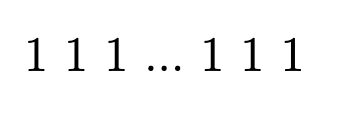
Мы можем ставить перегородку между двумя единичками. Если мы поставили перегородку, то мы "разбили" число на два слагаемых (от края/перегородки до следующей перегородки/края). Т.е. если мы хотим получить c слагаемых, мы должны расставить (c-1) перегородку. Позиций у нас всего (m-1). Тогда всего способов разбить число m на c положительных слагаемых будет

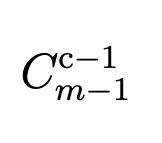
Теперь у нас есть разбиение числа m на с слагаемых:

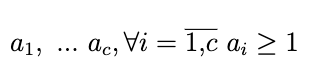
Если мы добавим каждому слагаемому единицу, то получим:

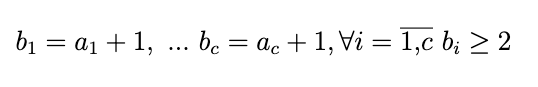
Т.е. если мы хотим разбиение числа m при условии, что слагаемые могут быть нулевыми, то мы можем посчитать разбиение суммы m+c на положительные слагаемые. Т.е. для фиксированного числа кирпичей ответ будет

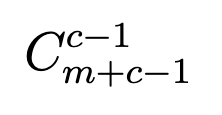
Тогда наш ответ это:

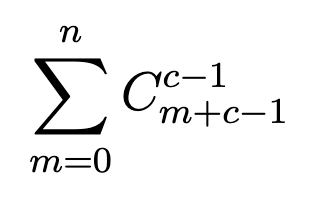
Пока зафиксируемся и отвлечёмся.

Есть такая замечательная формула, которая называется hockey-stick identity. Она похожа на хоккейную клюшку, если посмотреть на треугольник Паскаля:

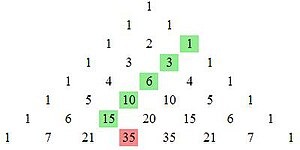
Сама формула выглядит так:

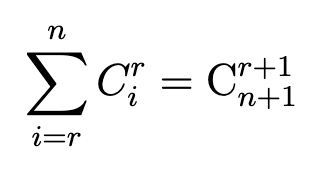
Вернёмся к нашей сумме и преобразуем её:

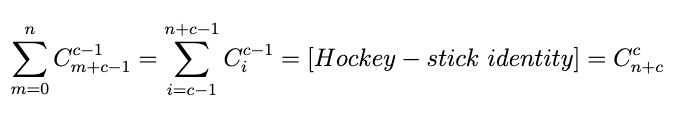
Только тут учтена стена, в которой использовано ноль кирпичей. Не забудем отнять единичку:

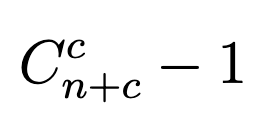
Круто! Осталось посчитать. Наше сочетание, как известно, можно посчитать через факториал:

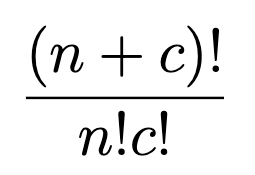
Т.к. ответ в задаче нужно дать по модулю простого числа, то можем воспользоваться малой теоремой Ферма:

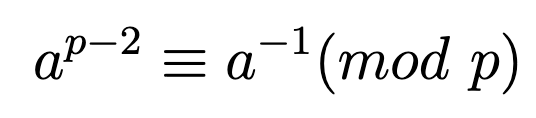
Т.е. вместо вычисления ответа нам не нужно считать огромные факториалы, аккуратно их делить друг на друга. Мы можем просто вычислить (n+c)! mod p, (n!)^(p-2) mod p и (c!)^(p-2) mod p (возведение в степень конечно лучше бинарное). Потом перемножить три составляющие по модулю, отнять единицу и ответ готов!