Задача Валерия Казакова
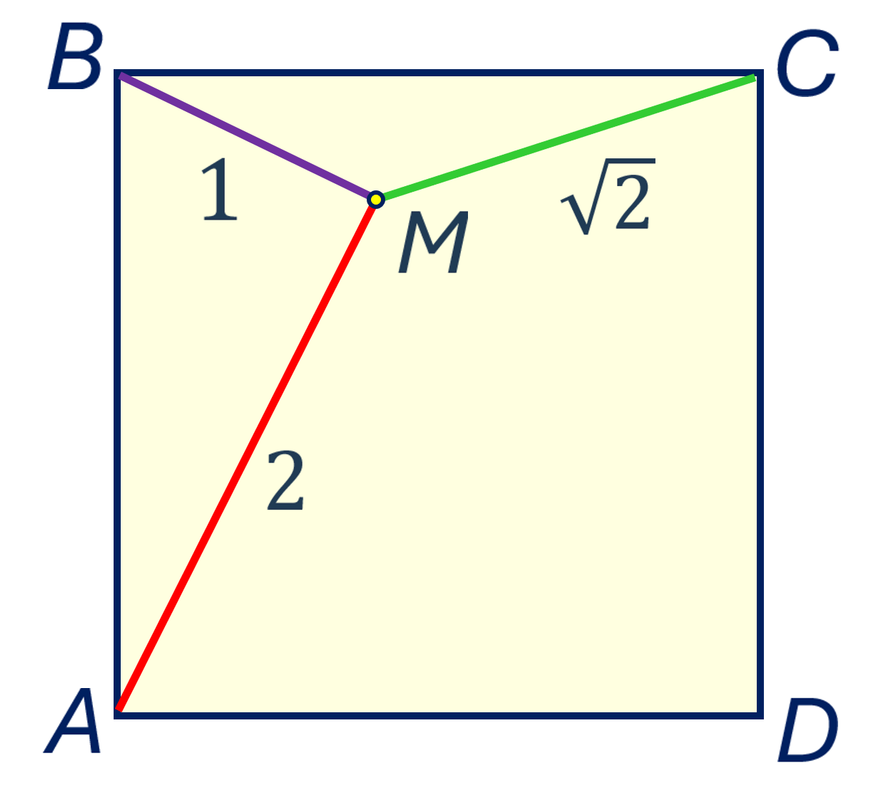
Задача. ABCD — квадрат. Точка М расположена внутри квадрата и удалена от вершины А на расстояние 2, от В — на 1, от С — на √2. Найти площадь квадрата.
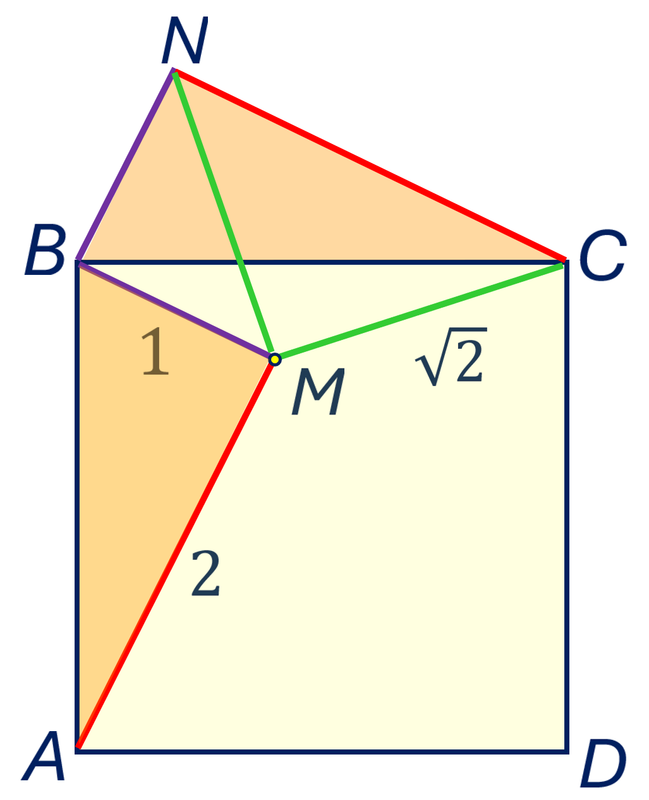
Решение 1. Повернём треугольник АВМ на 90° вокруг вершины В. При этом точка М перейдёт в некоторую точку N, а треугольник ВМА — в треугольник BNC. Треугольник MBN — прямоугольный равнобедренный, в нём MN = √2, ∠BNM = 45°.
Стороны треугольника CMN равны √2, √2 и 2, значит, он тоже прямоугольный и равнобедренный, в нём ∠МNС = 45°.
Отсюда видим, что ∠BMА = ∠BNС = 45°+ 45° = 90°. Треугольник ВМС — прямоугольный, и сторона квадрата АВ равна √5, а площадь квадрата равна 5.
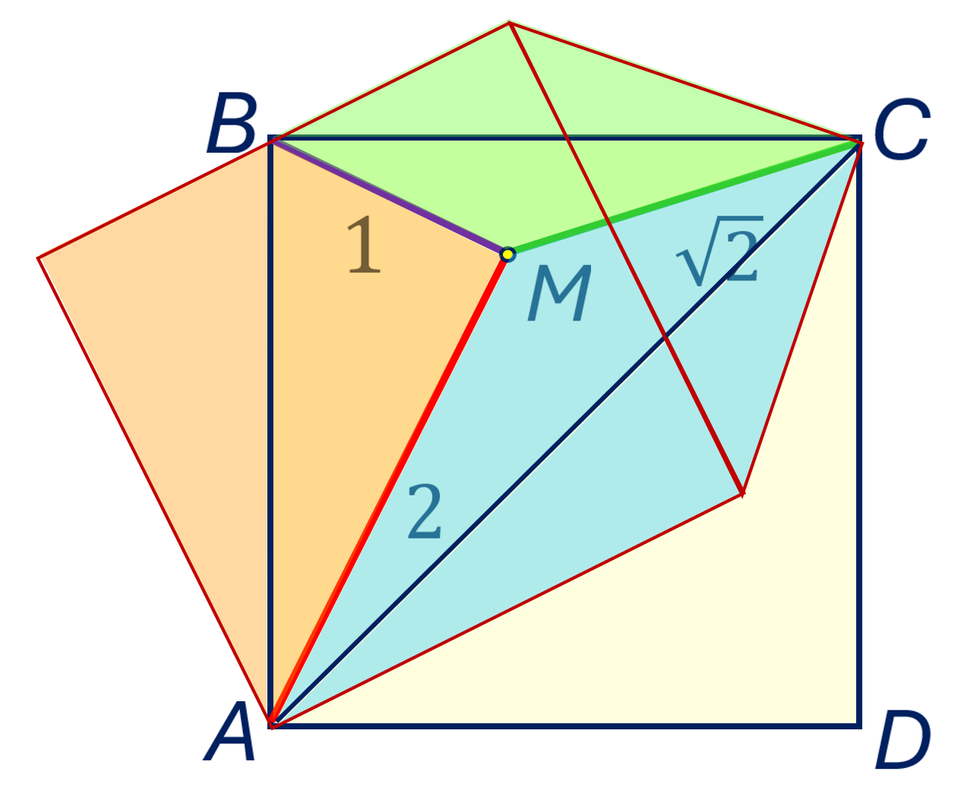
Решение 2. Отразим треугольник АМВ относительно стороны АВ, треугольник ВМС — относительно стороны ВС, а треугольник АМС — относительно стороны ВС. Рассмотрим пятиугольник, составленный из указанных трёх внутренних треугольников квадрата и симметричных им. Он состоит из квадрата со стороной 2 и равнобедренного прямоугольного треугольника со стороной √2. При этом его площадь в два раза больше половины площади данного квадрата, т.е. равна площади квадрата. Отсюда легко получаем ответ.
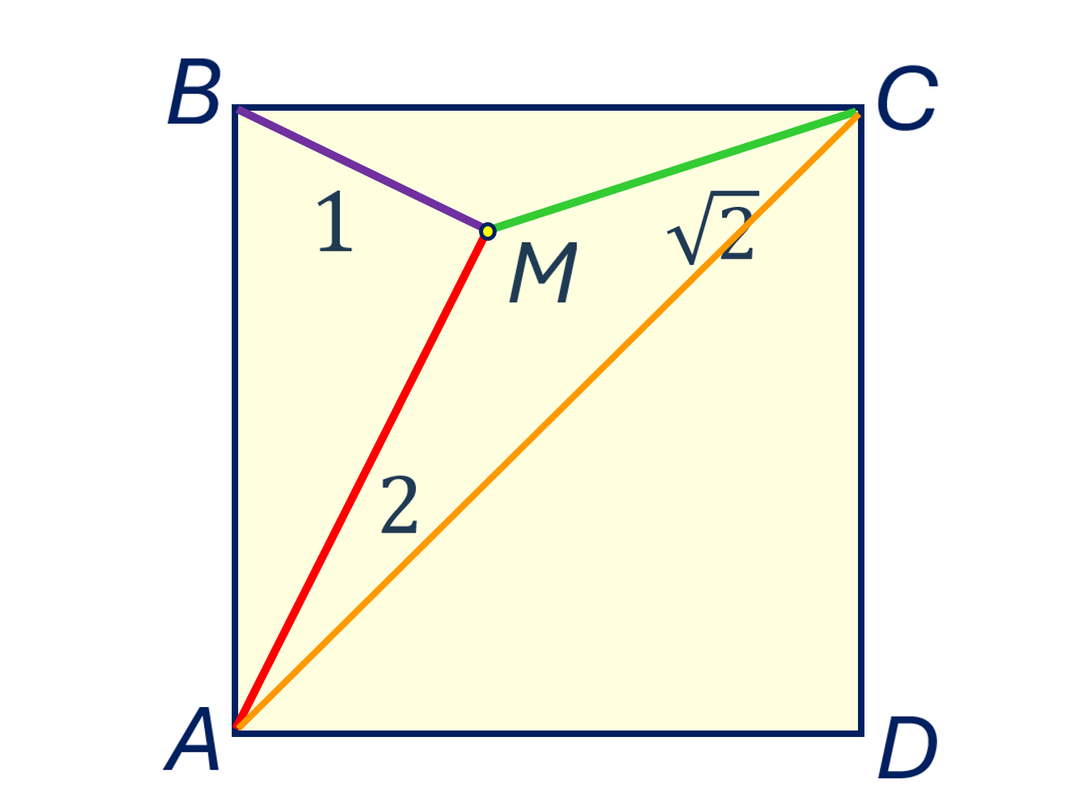
Решение 3. Треугольники СМА и ВМС подобны по трём сторонам с коэффициентом подобия √2.
Отсюда ∠MАС + ∠MСА = 45°. А значит, ∠АMС = ∠СМВ = 135°. Получаем ∠BMА = 90° и вычисляем сторону квадрата по теореме Пифагора.
Решение 4. Примем сторону квадрата за а; его площадь равна a².
Обозначим угол ВСМ за α. Тогда угол АВМ равен 90°– α.
Запишем теорему косинусов для треугольников ВСМ и АВМ:
(√2)² = 1 + a² – 2a cos α,
2² = 1 + a² – 2a sin α.
Отсюда следует уравнение:
4a² = (a²–1)² + (a²–3)².
Получилось квадратное уравнение про площадь квадрата, корнями которого служат 1 и 5. Внутреннему расположению точки М соответствует значение 5.
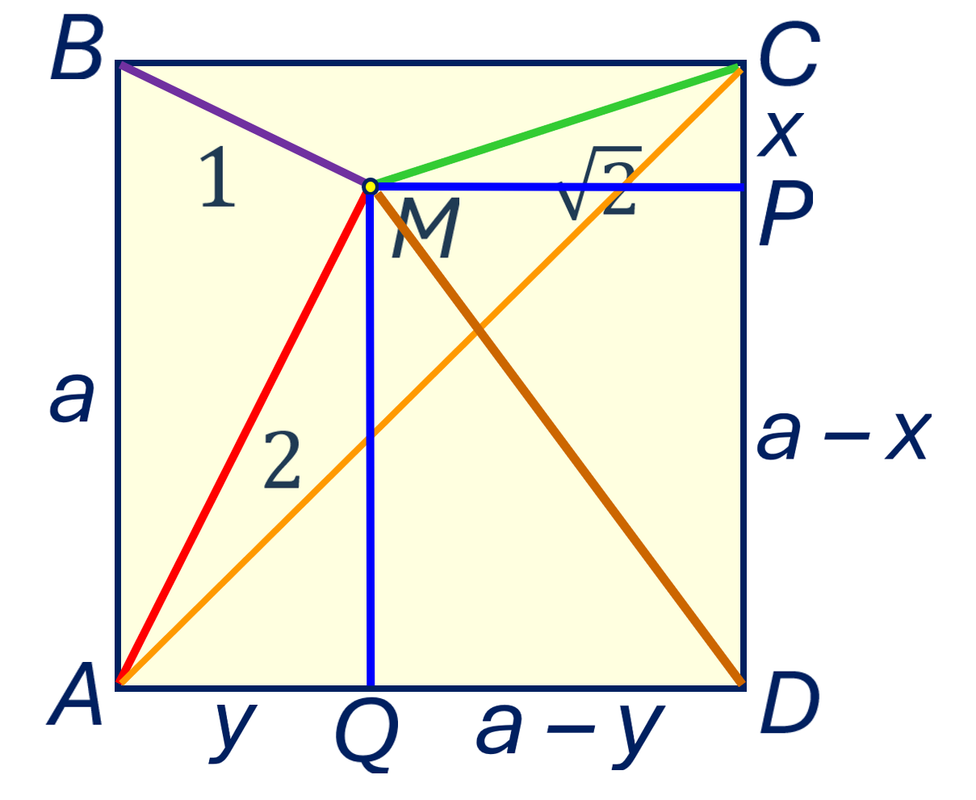
Решение 5. С помощью теоремы Пифагора легко показать, что для любой точки М и квадрата (и даже прямоугольника ABCD) выполняется равенство:
AM² + CM² = BM² + DM².
Отсюда найдём: DM² = 5.
Пусть P — ортогональная проекция точки М на СD, Q — её проекция на AD. Обозначим x = CP, y = AQ, a — сторона квадрата. Тогда
DP² + DQ² = DM²,
(a – x)² + (a – y)² = 5,
2a² – 2a(x + y) = 4,
a(x + y)/2 = a²/2 – 1.
В левой части полученного равенства стоит сумма площадей треугольников АВМ и ВМС, и она равна половине площади квадрата за вычетом 1. Это означает, что площадь треугольника АМС равна 1. Но тогда синус угла АМС равен √2/2, и, поскольку этот угол тупой, он равен 135°.
Отсюда заключаем, что точка М находится на окружности с центром D и радиусом, равным стороне квадрата, т.е. AD = DM = √5.