Задача М.Гарднера
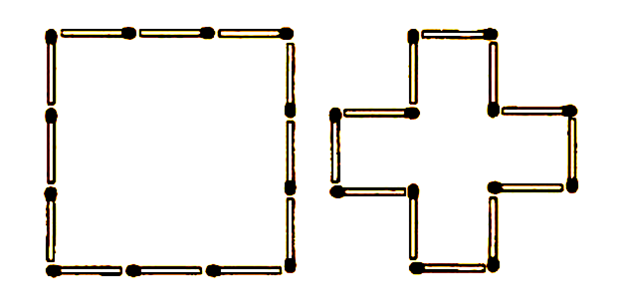
Если считать, что спичка служит эталоном длины (её длина принята за единицу), то 12 спичек можно различными способами расположить на плоскости так, чтобы получились многоугольники с целочисленной площадью. Например, легко построить квадрат с площадью 9 или крест с площадью 5.
Пользуясь всеми 12 спичками (длина каждой спички должна быть использована полностью), требуется выложить периметр многоугольника, площадь которого равна 4.
Возможные решения.
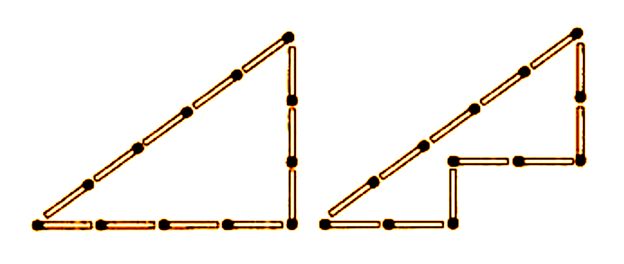
Из двенадцати спичек можно построить прямоугольный треугольник со сторонами в 3, 4 и 5 единиц. Изменив положение трёх спичек так, как показано на правом рисунке, мы уменьшим площадь фигуры на две квадратные единицы. Получится многоугольник с площадью, равной 4 квадратным единицам.
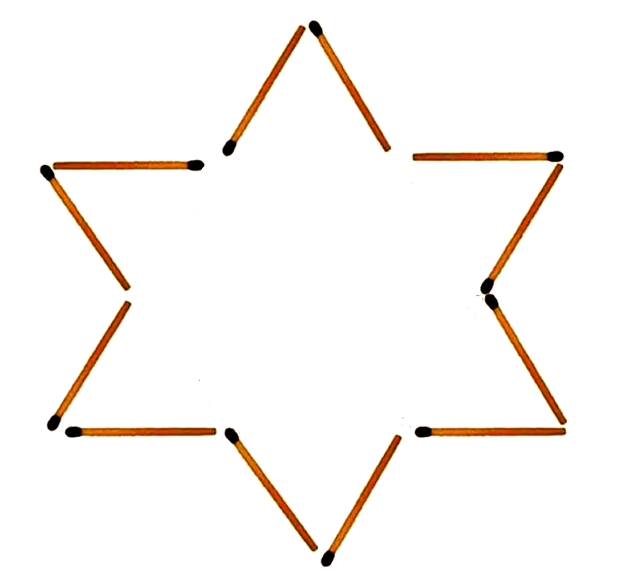
Возможно решение в виде звезды. Подбирая ширину лучей, можно получать звезду любой площади: от 0 до 3·(2+√3) ≈ 11,196 квадратных единиц — площади правильного 12-угольника, наибольшей площади, которую можно ограничить периметром длиной в 12 спичек.
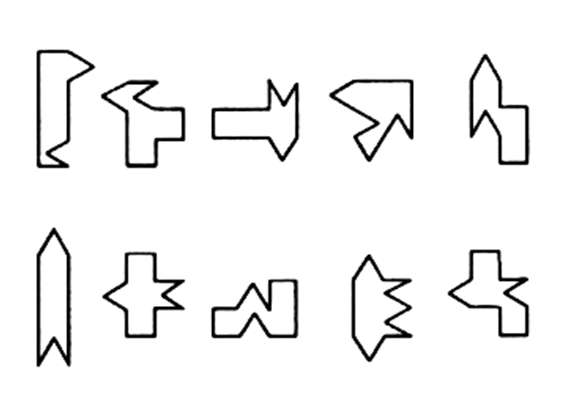
Множество решений также позволяет найти каждая из фигур тетрамино (состоящая из четырёх единичных квадратов). Нужно лишь отбрасывать квадраты, заменяя их равновеликими по площади треугольниками до тех пор, пока длина периметра получившейся фигуры не достигнет 12 спичек.