Задача М.Гарднера
В углах квадрата со стороной 10 находится по таракану. Они начинают одновременно ползти: A к B, B к C, C к D и D к A. Если все четыре насекомых начнут двигаться одновременно с одинаковой скоростью, то они опишут четыре одинаковые логарифмические спирали, которые пересекутся в центре квадрата. Какое расстояние проползёт до встречи каждый таракан? (Задача решается без вычислений.)
Тот же вопрос, если три таракана сидят в вершинах правильного треугольника.
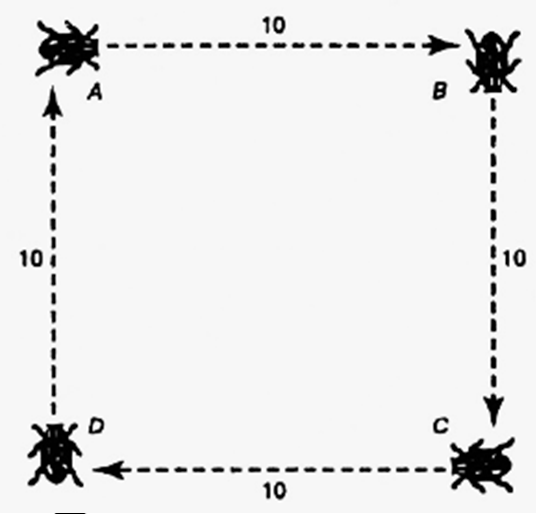
Решение. В любой момент времени тараканы находятся в вершинах квадрата, который сжимается и поворачивается по мере их сближения друг к другу. Поэтому путь преследователя всегда будет перпендикулярен пути преследуемого. А это значит, что если А приближается к В, то скорость В не имеет компоненты вдоль направления скорости А, т.е. В в результате своего движения никак не может оторваться от А или приблизиться к нему. Следовательно, А поймает В через такой же промежуток времени, как если бы В стоял на месте. Длина каждой спирали будет равна стороне квадрата —10.
Если бы три таракана выползали из вершин правильного треугольника, то составляющая скорости каждого, направленная к его преследователю, была равна половине всей скорости таракана (т.к. cos 60° = ½ ). Поэтому тараканы будут сближаться со скоростью ³⁄₂, если за единицу принять скорость таракана относительно поверхности стола. Тараканы встретятся в центре треугольника через промежуток времени, равный отношению стороны треугольника к утроенной скорости таракана. Каждый таракан при этом проползет расстояние, равное ⅔ стороны треугольника.