Задача 5
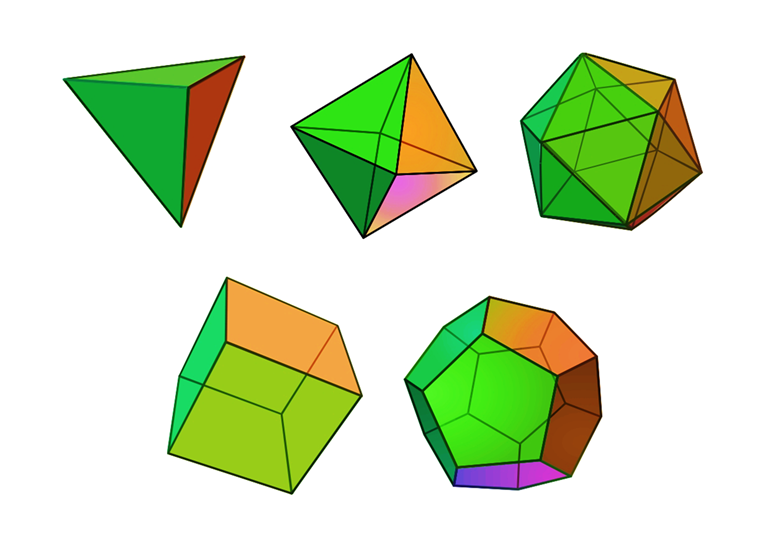
Теорема. Докажите, что существует ровно 5 типов правильных многогранников.
Решение. По определению правильного многогранника все его грани должны быть правильными n-угольниками; в каждой его вершине сходится одинаковое число рёбер, пусть m. При этом n≥3 и m≥3 .
(Полную классификацию многогранников для пространств размерности k впервые дал Людвиг Шлефли; с тех пор в научный оборот вошел т.н. символ Шлефли {n, m}, где n — количество углов в грани, m — количество граней, которые сходятся в вершине.)
Подсчитаем число рёбер по граням. Все грани — n -угольники, число граней равно Г, тогда nГ даёт удвоенное число рёбер, так как каждое ребро прилегает к двум многоугольникам. Итак, Г = 2Р/n.
Подсчитаем число рёбер по вершинам. В каждой вершине сходятся m рёбер, число вершин равно В, тогда mВ даёт удвоенное число рёбер, так как каждое ребро соединяет две вершины. Получаем В = 2Р/m.
Согласно формуле Эйлера: В – Р + Г = 2. Подставляя сюда найденные значения для числа граней и вершин, получим:
2Р/m – Р + 2Р/n = 2,
или
(2n – mn + 2m)·Р = 2mn.
Отсюда видно, что 2n – mn + 2m > 0,
что равносильно
(n – 2)( m – 2) < 4.
Ясно, что это неравенство имеет лишь следующие пять решений (n; m):
(3; 3) — тетраэдр;
(4; 3) — куб;
(3; 4) — октаэдр;
(5; 3) — додекаэдр;
(3; 5) — икосаэдр.
Утверждение доказано.