Задача 3
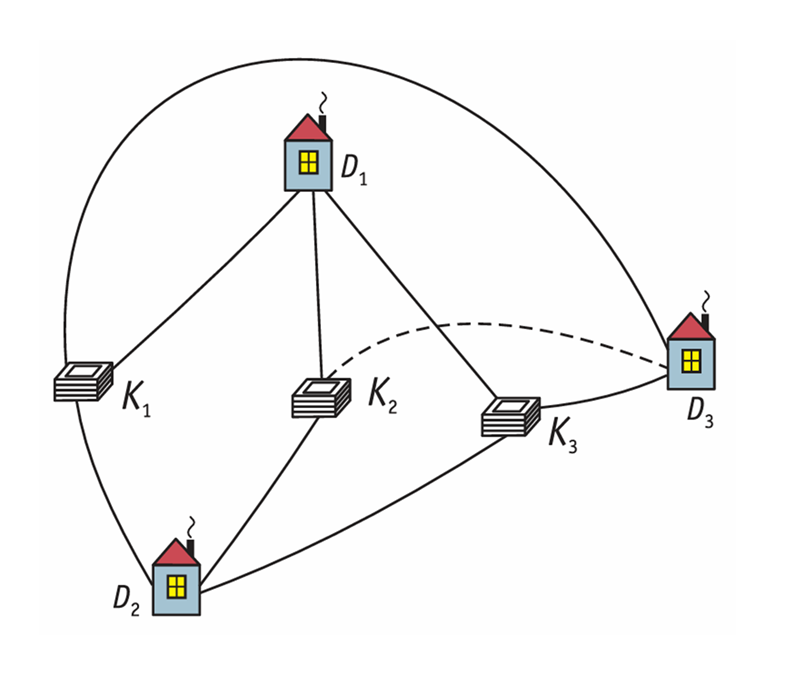
Три соседа имеют три общих колодца. Можно ли провести не пересекающиеся дорожки от каждого дома к каждому колодцу?
Решение. Предположим, что это сделать можно. Каждый домик соединим с каждым колодцем так, чтобы 9 получившихся линий попарно не пересекались. Всякие две точки, изображающие дома или колодцы, будут соединены отрезками, которые, в силу теоремы Эйлера, разделят ограниченную ими часть плоскости на 9 – 6 + 2 = 5 областей. Каждая из пяти областей ограничена четырьмя отрезками, так как, по условию, ни одна из дорожек не должна непосредственно соединять два дома или два колодца. Поэтому число линий, ограничивающих эти пять областей, должно быть не меньше 5 ⋅ 4 / 2 = 10, а по условию их число равно 9. Получаем противоречие с условием. Следовательно, нельзя провести не пересекающиеся дорожки от каждого дома к каждому колодцу.