W-функция Ламберта и ее приложения

Введение

Математический анализ знает множество прекрасных функций с необычными свойствами. Среди них интегральные синус

и логарифм

, также нельзя не отметить гамма-функцию

или очень известную дзета-функцию Римана

. Но сегодня я предлагаю читателю посмотреть на функцию W-Ламберта

Что такое W-функция Ламберта?

Для того, чтобы понять, что такое W-функция Ламберта, достаточно посмотреть на следующее равенство, которое по аналогии с основным тригометрическим тождеством предлагаю именовать "основное Ламбертово тождество":

Другими словами, функция Ламберта - обратная для

. Однако после первых же исследований станет понятно, что

не инъективна, а именно одно и то же значение

достигается при двух разных аргументах, если

. Поэтому данное выше определение требует пояснений.

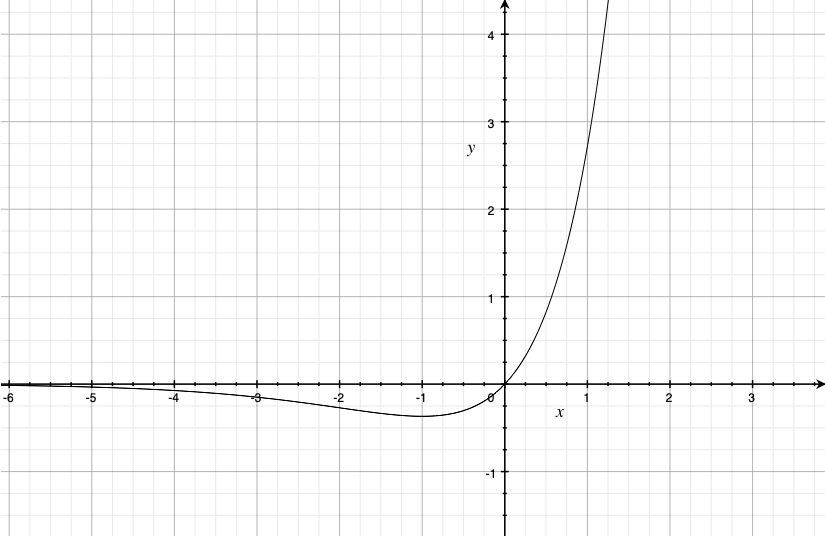
Исследовав производную функции

, понимаем, что функция возрастает на

и убывает на

. Таким образом, давайте построим обратную функцию к данной на соответствующих промежутках монотонности.

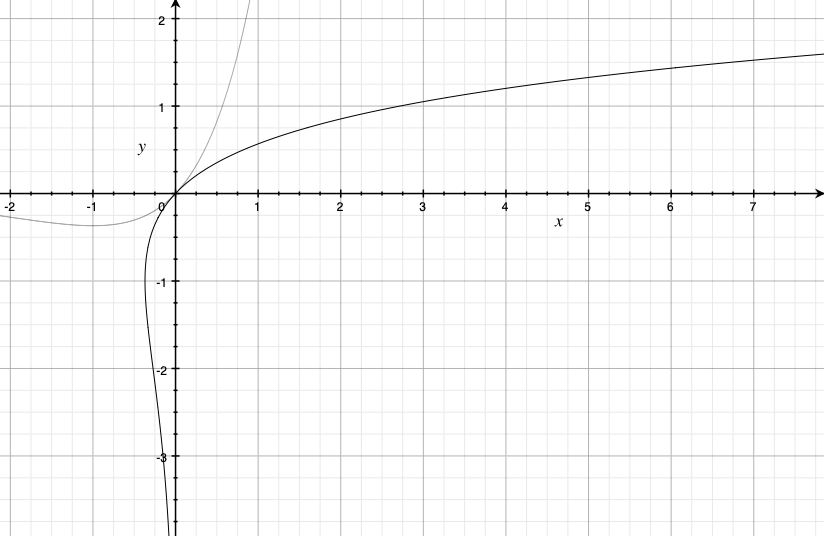
Графики W-функции Ламберта (черный) и y = xe^x (серый)

Ветвь, для которой

, называется

, другая -

Постановка задачи

Задача. Научиться находить действительные корни уравнения следующего вида:

x^pe^x=q \\p \in \mathbb{Q} \ \backslash \ \mathbb{Z}, q\in\mathbb{R_{+}}

Как вы, наверное, уже догадались, для решения будем использовать W-функцию Ламберта. Итак, сначала возведем и левую, и правую часть в степень

(это преобразование не является равносильным при четных целых

, а при нечетных нужно будет расширять множество значений

до всех действительных чисел, поэтому решаем задачу для указанных выше ограничений).

Теперь для того, чтобы воспользоваться основным Ламбертовым тождеством, нам нужно получить выражение с

такое, как и в показателе степени экспоненты. Для этого поделим и левую, и правую часть на

\frac{x}{p}e^{\frac{x}{p}}=\frac{q^{\frac{1}{p}}}{p}

И теперь мы можем воспользоваться основным Ламбертовым тождеством:

Откуда и получаем уже итоговую формулу для

Вычисление W-функции Ламберта

Заметим, что при

функция Ламберта дает два действительных значения: по одному на каждой из ветвей

соответственно. В этом случае у изначального уравнения будет 2 корня.
Вычисление W0. Будем использовать метод бинарного поиска по ответу. Мы можем так поступить, поскольку

возрастает на

.
Левая граница бинарного поиска понятна и равна

. Теперь возникает вопрос, как выбрать правую границу. Первая идея, которая приходит на ум: положить ее равной

, ибо верно неравенство

, причем равенство достигается только в нуле.

x \geq W(x) \iff x \geq \frac{x}{e^{W(x)}} \iff (e^{W(x)}-1)x \geq0

Однако для достаточно больших

это может быть не лучшим вариантом. Поэтому давайте посмотрим на другой: выберем правую границу равной

ln(x) \geq W(x) \iff x \geq e^{W(x)} \iff x\geq \frac{x}{W(x)} \iff x(\frac{W(x)-1}{W(x)})\geq0 \\ x\geq e

Итого: при

правой границей выбираем

, а при

берем

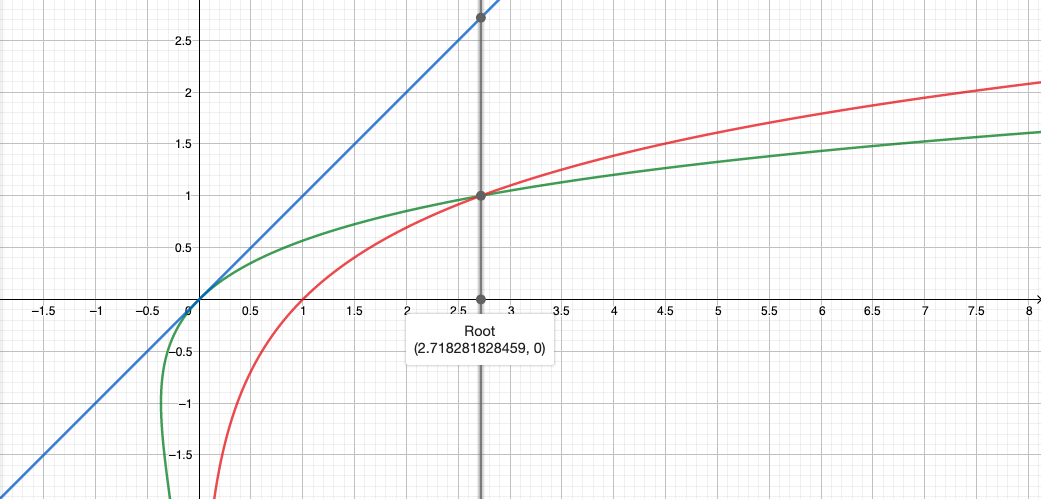
Графики y = x (синий), y = W(x) (зеленый) и y = ln(x) (красный)

Ассимптотика:

, prec - изначально выбранная точность (например, 10-12)
Вычисление W-1. Здесь будем использовать следующее бесконечное выражение для

W_{-1}(x)=ln\frac{-x}{-ln\frac{-x}{\dots}}

Чем глубже мы спускаемся, тем выше точность вычислений.

Реализация на Python

from math import *

def LambertW0(x):
    left = -1
    right = x if x <= e else log(x)
    prec = 10**-12 # точность
    # бинарный поиск
    while right - left > prec:
        mid = (right + left) / 2
        if mid * exp(mid) > x:
            right = mid
        else:
            left = mid
    return right

def LambertW_1(x, t): # t - показатель точности
    if t == 100:
       return log(-x)
    else:
       return log((-x)/(-LambertW_1(x, t + 1)))

def sol(p, q):
    s = q**(1/p) / p
    if s < -exp(-1):
        return "No real solutions"
    ans = "Solutions: " + str(p * LambertW0(s)) + " "
    if -exp(-1) < s and s < 0:
       ans += str(p * LambertW_1(s, 0))
    return ans
    

p = float(input())
q = float(input())
print(sol(p, q))

Проверка

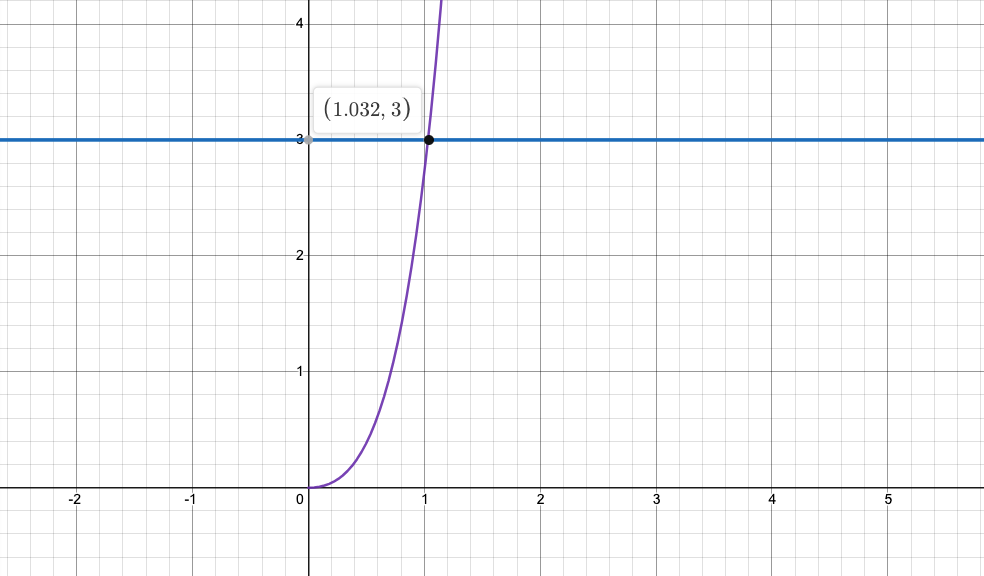
Уравнение 1.

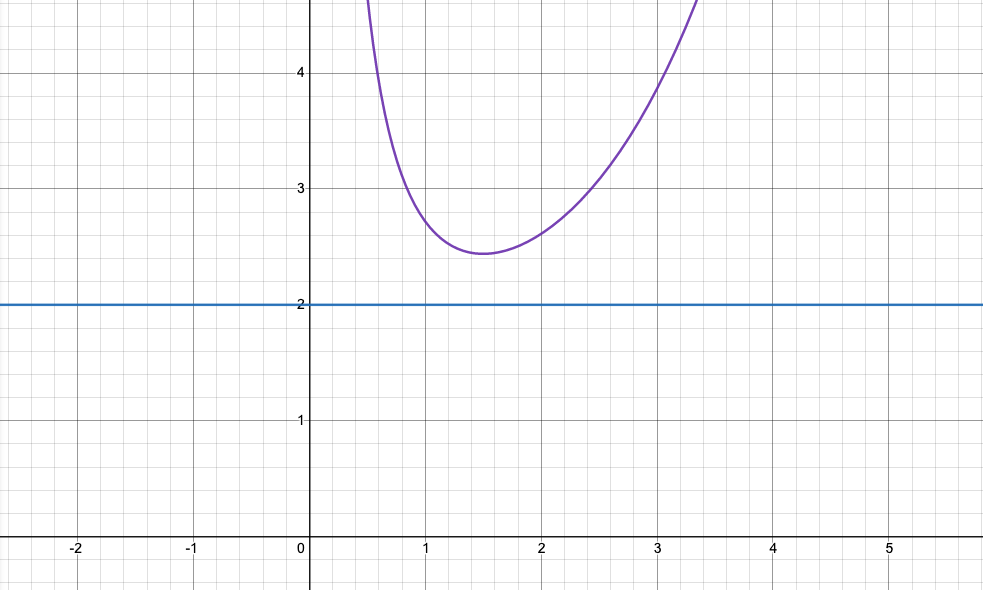
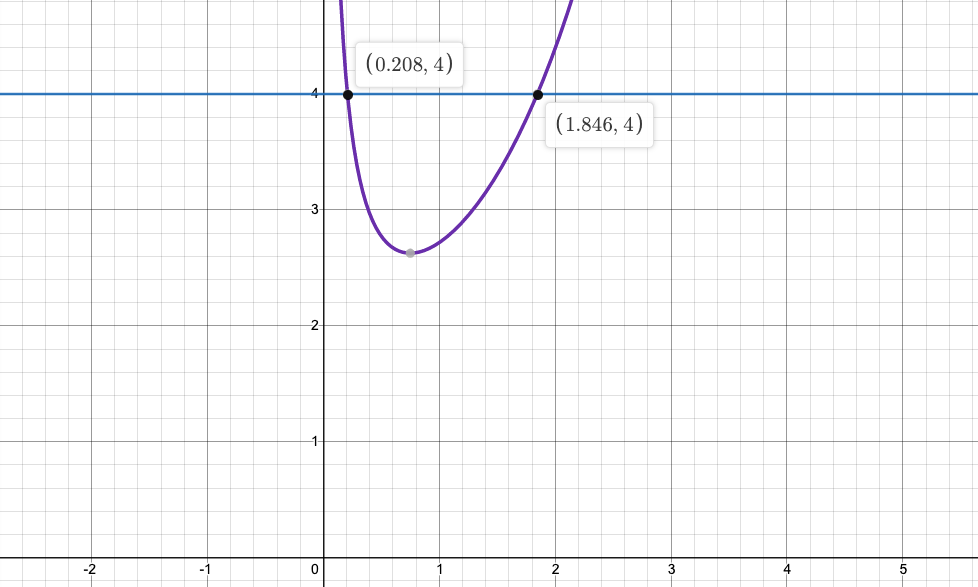
Графики y = x^(-1.5)*e^x (фиолетовый) и y = 2 (синий)

Уравнение 2.

Графики y = x^2.1*e^x (фиолетовый) и y = 3 (синий)

Уравнение 3.

Графики y = x^(-0.75)*e^x (фиолетовый) и y = 4 (синий)

Заключение / выводы

Значения на 0 и -1 ветви W-функции Ламберта могут быть достаточно точно вычислены за короткое время, что делает возможным решение некоторых типов уравнений.