Возвращение к истокам, часть третья: Логистическая регрессия
Сегодня мы попрощаемся с данной серией статей, первые две части вы можете найти тут
https://telegra.ph/Vozvrashchenie-k-istokam-chast-pervaya-Linejnaya-regressiya-i-celevaya-funkciya-03-16 – 1 часть
https://telegra.ph/Vozvrashchenie-k-istokam-chast-vtoraya-Gradientnyj-spusk-03-23 – 2 часть
Сейчас стало меньше свободного времени, поэтому перевода так давно не было. Канал забрасывать не планирую, особенно после такого массового прироста аудитории) Спасибо Вам!
Вышло довольно интересно и, как всегда в статьях этого цикла, визуально красиво. Приятного чтения.
Оригинал статьи https://towardsdatascience.com/back-to-basics-part-tres-logistic-regression-e309de76bd66
Переведено для https://t.me/letsdatanow
Добро пожаловать в заключительную часть нашей серии "Назад к основам", где мы рассмотрим еще один фундаментальный алгоритм машинного обучения: Логистическая регрессия. В предыдущих двух статьях мы помогли нашему другу Марку определить идеальную цену продажи его дома площадью 2400 футов² с помощью линейной регрессии и градиентного спуска.
Сегодня Марк снова обратился к нам за помощью. Он живет в модном районе, где, по его мнению, дома меньше определенного размера не продаются, и он беспокоится, что его дом тоже может не продаться. Он попросил нас помочь ему определить, насколько вероятно, что его дом будет продан.
Именно здесь в игру вступает логистическая регрессия.
Логистическая регрессия - это тип алгоритма, который предсказывает вероятность двоичного результата, например, продастся дом или нет. В отличие от линейной регрессии, логистическая регрессия прогнозирует вероятности, используя диапазон от 0% до 100%. Обратите внимание на разницу между прогнозами линейной и логистической регрессионной модели:

Логистическая регрессия: с вероятностью в 85% дом площадью 4000 квадратных футов. будет продан
Давайте углубимся в то, как работает логистическая регрессия, определив вероятность продажи домов разного размера.
Мы начнем наш процесс снова со сбора данных о размерах домов в районе Марка и посмотрим, продаются они или нет.
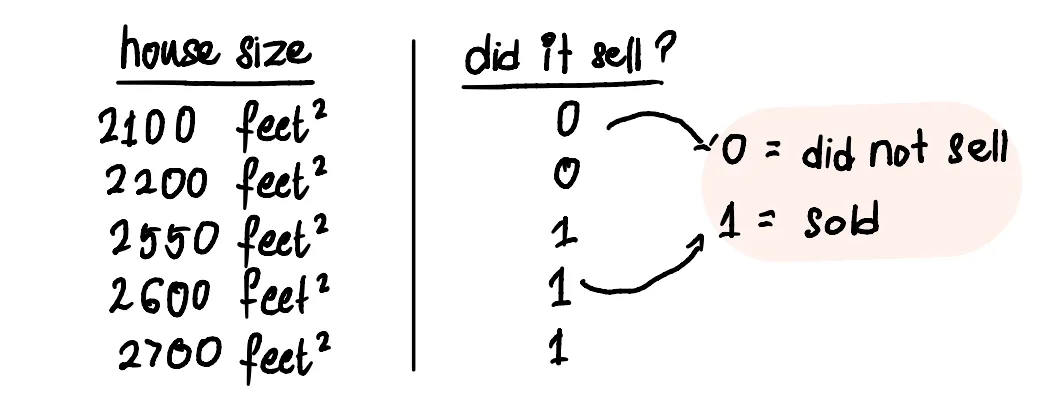
0 – не продан
1 – продан
Визуализируем
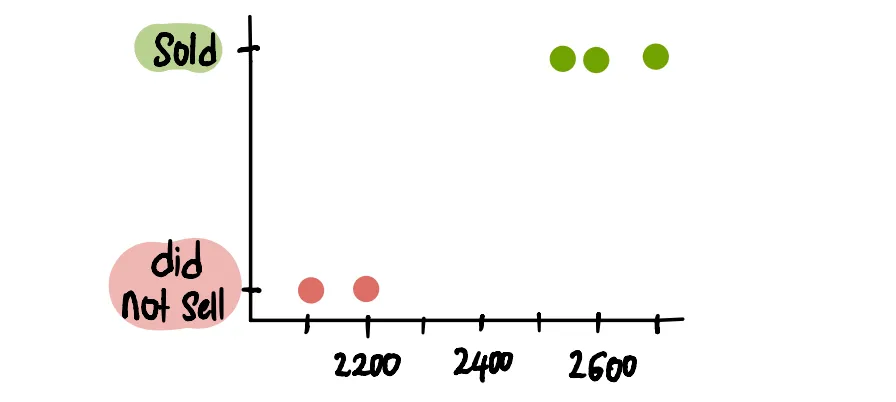
Вместо того чтобы представлять результат участка в виде двоичного набора, будет более информативным представить его с помощью вероятностей, поскольку именно это количество мы пытаемся предсказать.
Мы представляем 100% вероятность как 1, а 0% вероятность как 0.
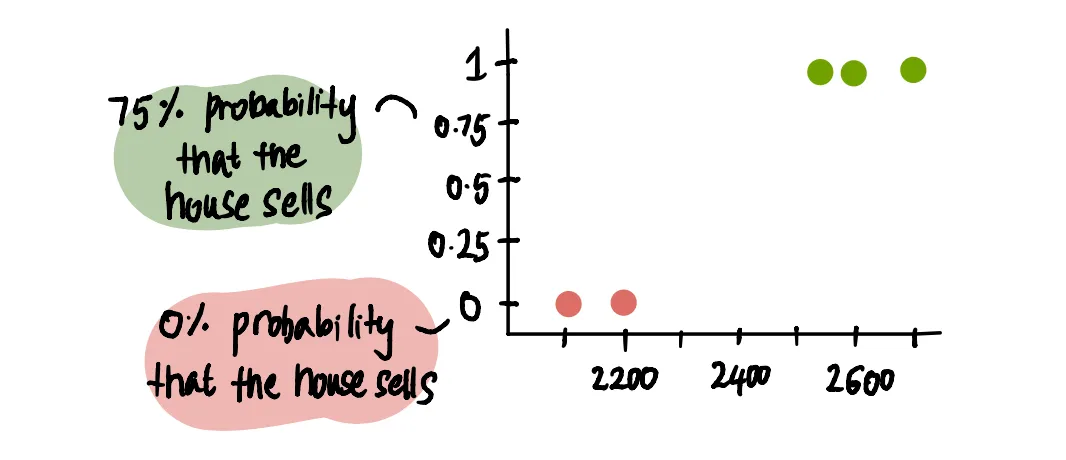
В нашей предыдущей статье мы узнали о линейной регрессии и ее способности подгонять линию к нашим данным. Но может ли она работать для нашей задачи, где желаемым результатом является вероятность? Давайте выясним это, попытавшись подогнать линию с помощью линейной регрессии.
Мы знаем, что формула для наиболее подходящей линии такова:
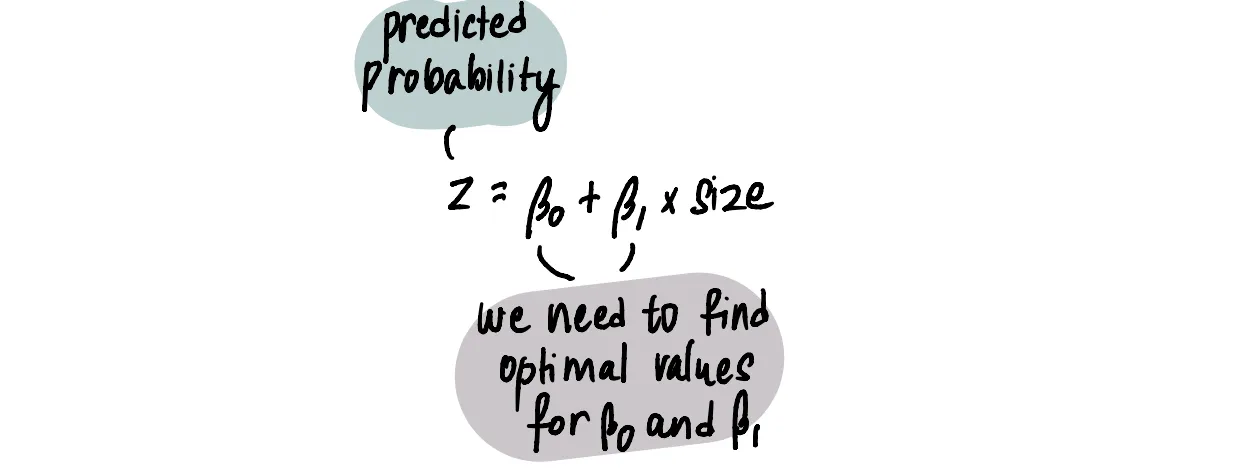
Нужно найти оптимальное значение для бета_0 и бета_1
Следуя шагам, описанным в линейной регрессии, мы можем получить оптимальные значения β₀ и β₁, что приведет к наилучшему результату. Предположив, что мы это сделали, давайте посмотрим на полученную линию:
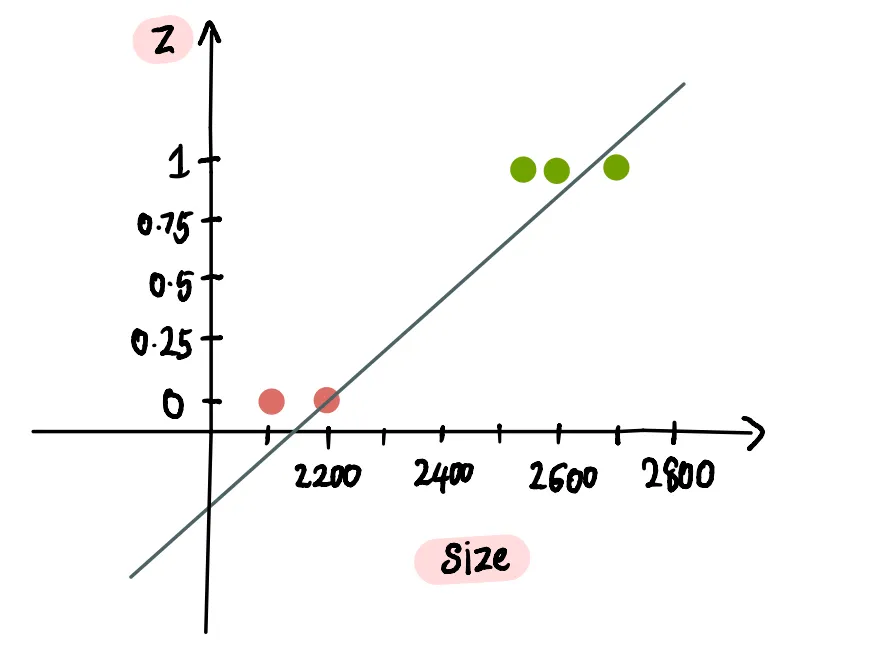
Исходя из этой линии, мы видим, что дом площадью чуть меньше 2700 футов² с вероятностью 100% будет продан:
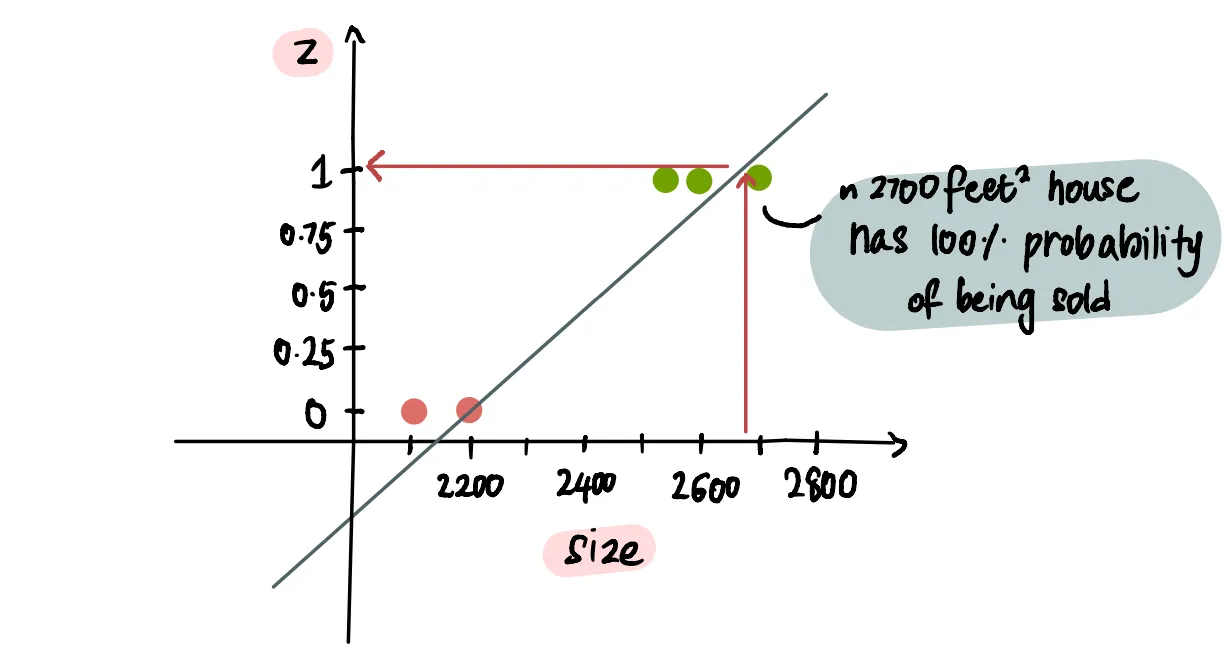
...а дом площадью 2200 футов², по прогнозам, имеет вероятность в 0% быть проданным:
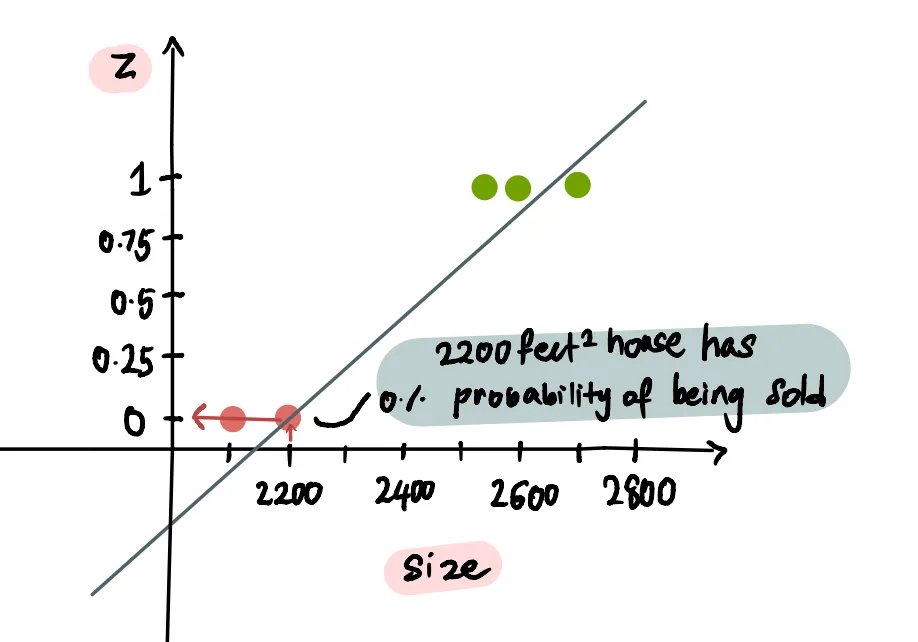
...а вероятность продажи дома площадью 2300 футов² составляет около 20%:
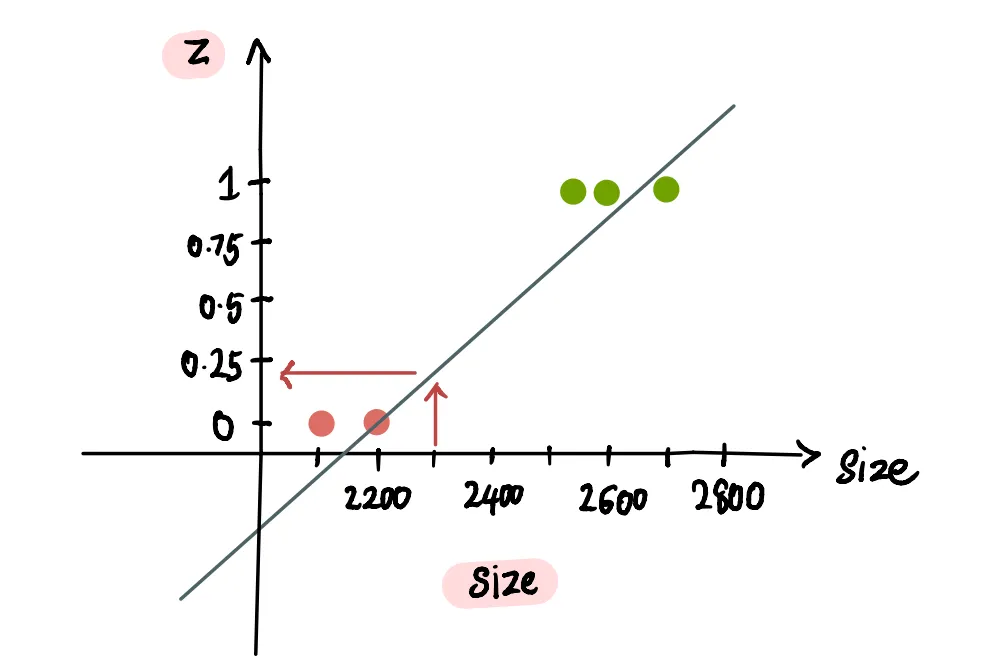
Итак, очевидно, что мы столкнулись с проблемой, поскольку прогнозируемая вероятность для дома площадью 2100 футов² отрицательна. Это определенно не имеет смысла и указывает на проблему с использованием стандартной линии линейной регрессии.
run into a problem – столкнуться с проблемой
Как мы знаем, диапазон вероятностей составляет от 0 до 1, и мы не можем выйти за пределы этого диапазона. Поэтому нам нужно найти способ ограничить наш прогнозируемый результат этим диапазоном.
constrain – сдержать, ограничить
Чтобы решить эту проблему, мы можем пропустить наше уравнение линейной регрессии через супер крутую штуку под названием *сигмоидная функция*. Эта функция преобразует наши прогнозируемые значения так, чтобы они попадали в диапазон от 0 до 1. Мы вводим наше значение z (где z = β₀ + β₁size) в нее..
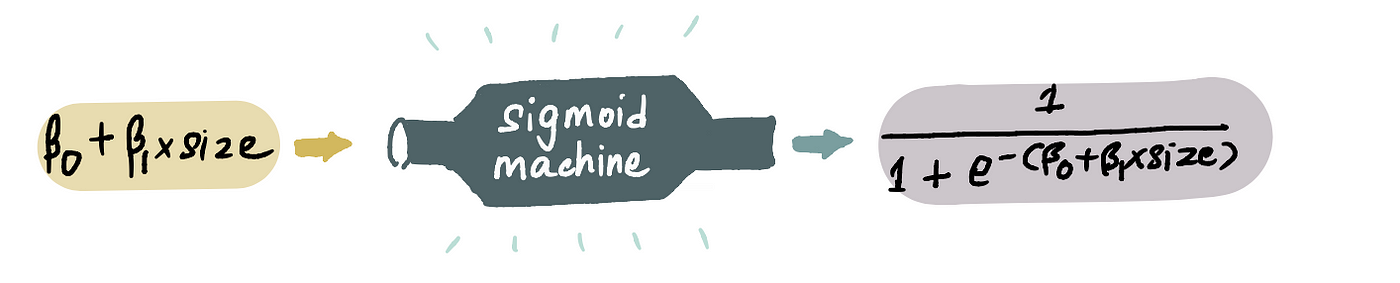
...и получаем новое причудливо выглядящее уравнение, которое соответствует нашим вероятностным ограничениям.
e – это число Эйлера и равно 2.718...
Более математически точный способ представления сигмоидной функции:
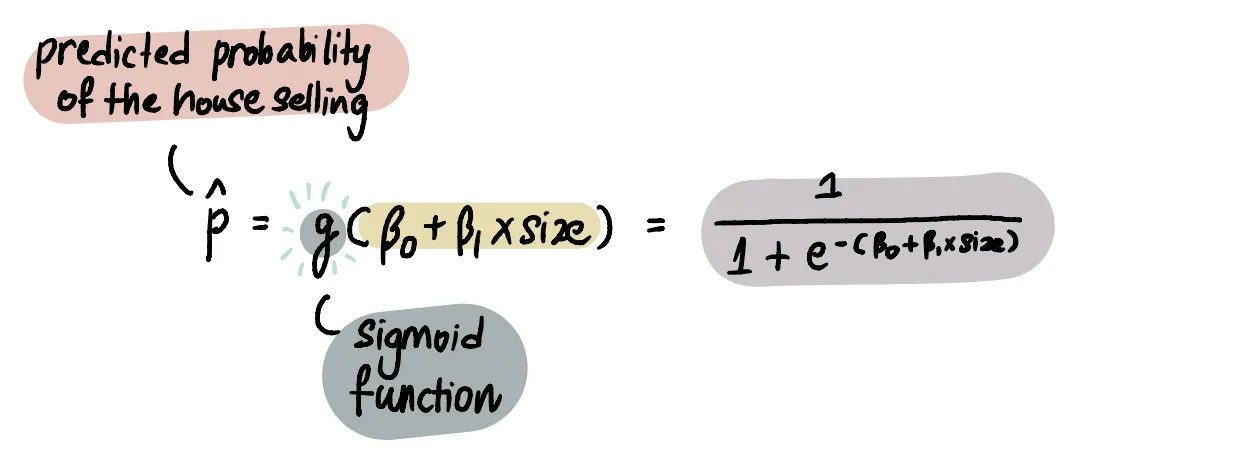
Если мы построим график, то увидим, что сигмоидная функция сжимает прямую линию в s-образную кривую, заключенную между 0 и 1.
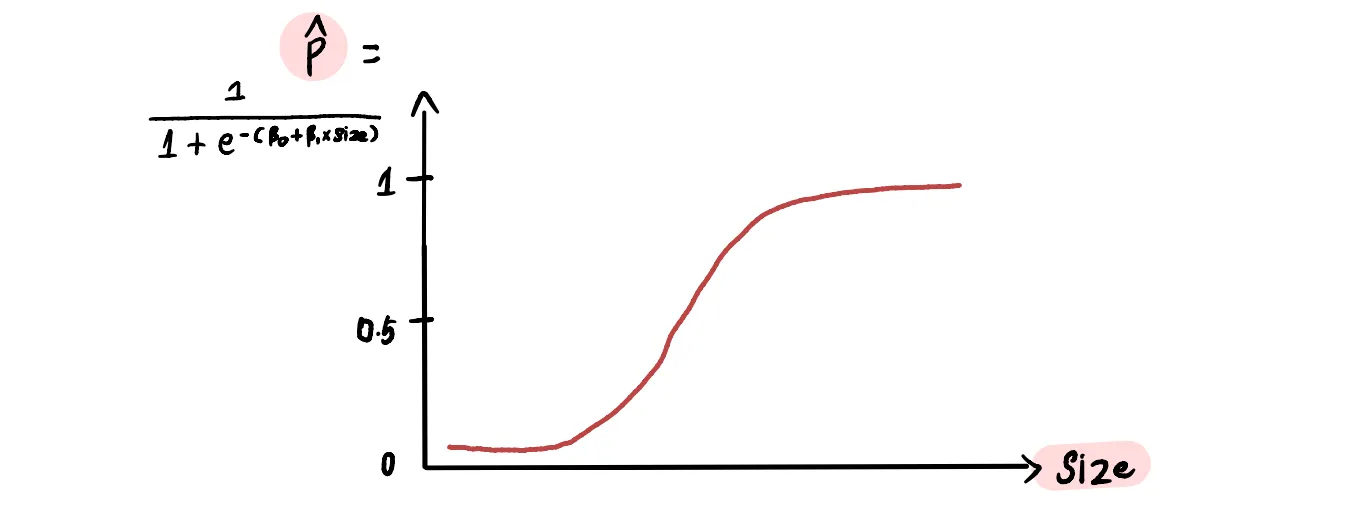
Необязательное примечание для всех моих математиков: Вам может быть интересно, почему и как мы использовали сигмоидную функцию для получения желаемого результата. Давайте разберемся.
Мы начали с неверного предположения, что использование формулы линейной регрессии даст нам желаемую вероятность.
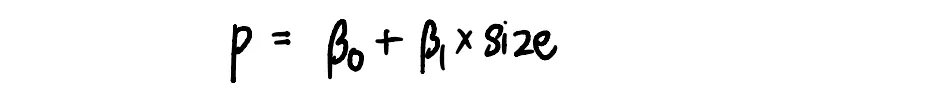
Проблема с этим предположением заключается в том, что (β₀ + β₁size) имеет диапазон (-∞,+∞), а p имеет диапазон [0,1]. Поэтому нам нужно найти значение, диапазон которого совпадает с диапазоном (β₀ + β₁size).
Чтобы решить эту проблему, мы можем приравнять линию к "log odds" (посмотрите это видео, чтобы лучше понять log odds), поскольку мы знаем, что log odds имеет диапазон (-∞,+∞).
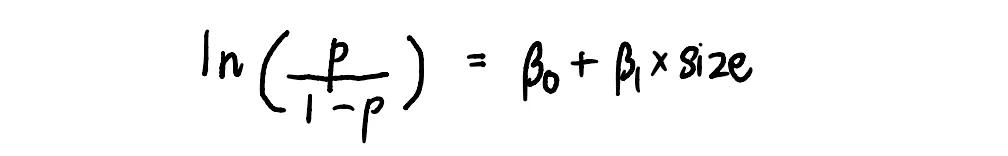
Ну а дальше дело техники:)
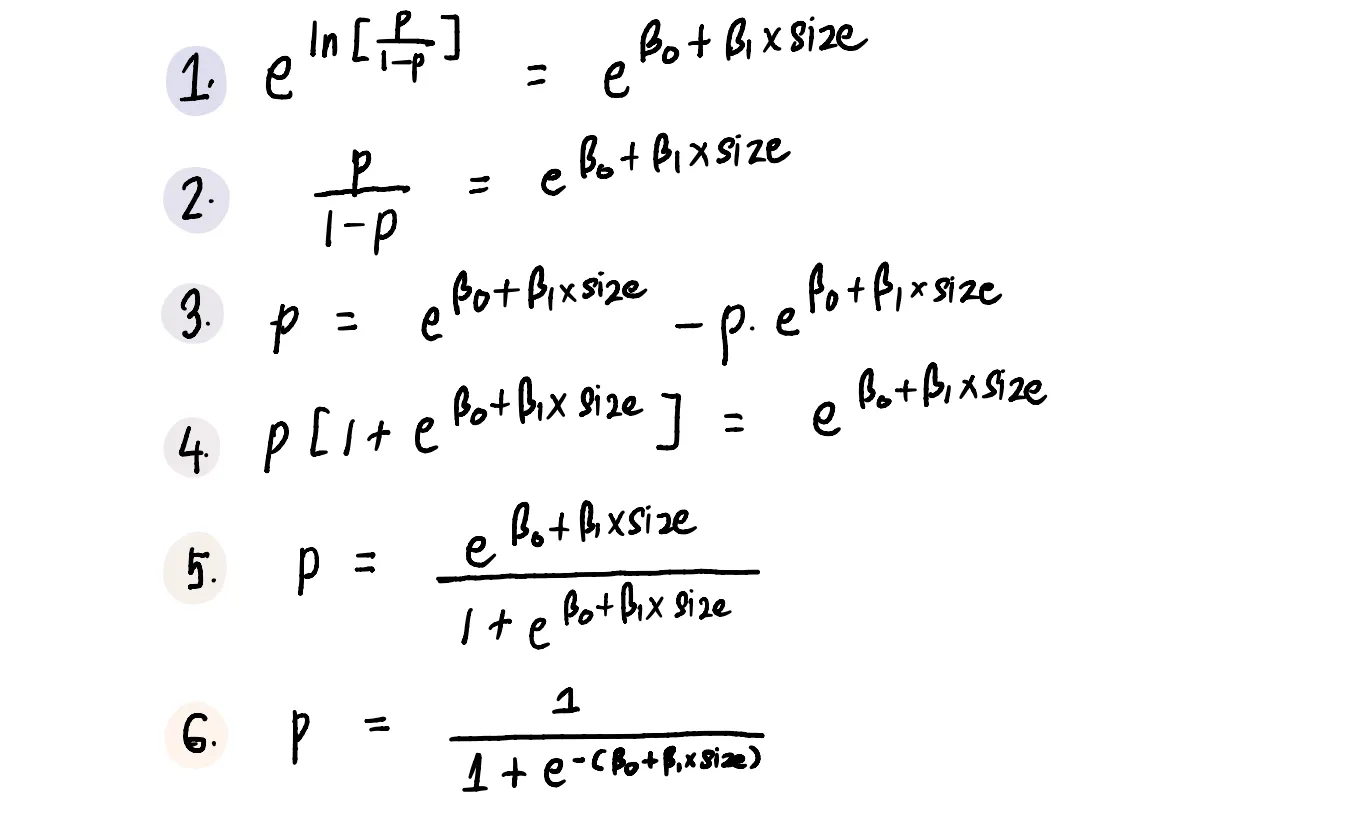
Теперь, когда мы знаем, как изменить линию линейной регрессии так, чтобы она соответствовала нашим ограничениям на выход, мы можем вернуться к нашей исходной задаче.
Нам нужно определить оптимальную кривую для нашего набора данных. Для этого нам нужно определить оптимальные значения для β₀ и β₁ (поскольку это единственные значения в уравнении прогнозируемой вероятности, которые изменят форму кривой).
Подобно линейной регрессии, мы будем использовать целевую функцию и алгоритм градиентного спуска для получения подходящих значений для этих коэффициентов. Однако ключевым отличием является то, что мы не будем использовать целевую функцию MSE, применяемую в линейной регрессии. Вместо этого мы будем использовать другую функцию под названием Log Loss, которую мы рассмотрим более подробно в ближайшее время.
Про градиентный спуск мы говорили во второй части, я ее переводил, текст есть тут
Допустим, мы использовали градиентный спуск и целевую функцию Log Loss (используя эти шаги), чтобы найти, что наши оптимальные значения β₀ = -120,6 и β₁ = 0,051, тогда наше уравнение прогнозируемой вероятности будет иметь вид:
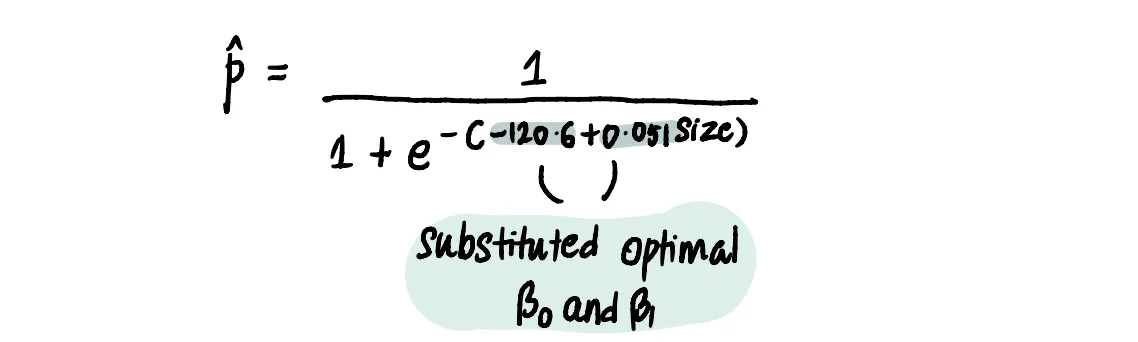
Получаем такую кривую вероятности
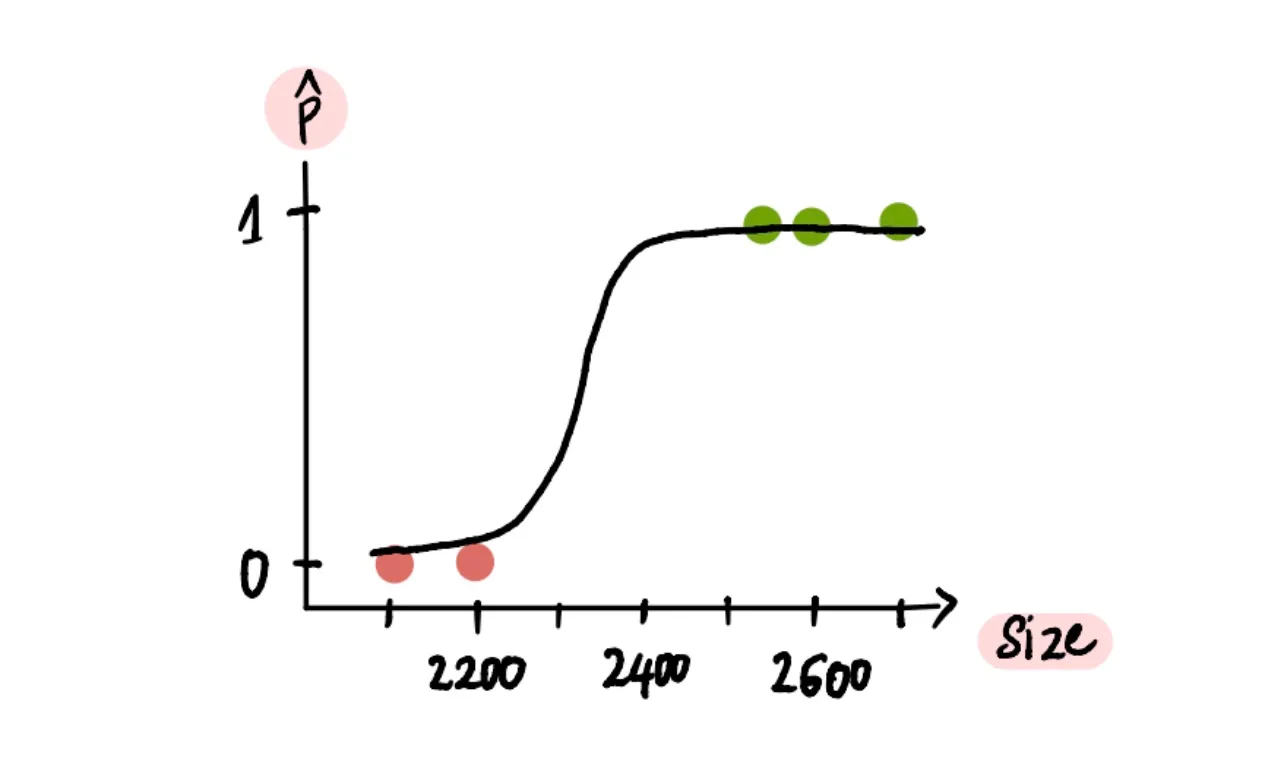
С помощью этой новой кривой мы можем теперь решить проблему Марка. Посмотрев на нее, мы увидим, что дом площадью 2400 футов²...
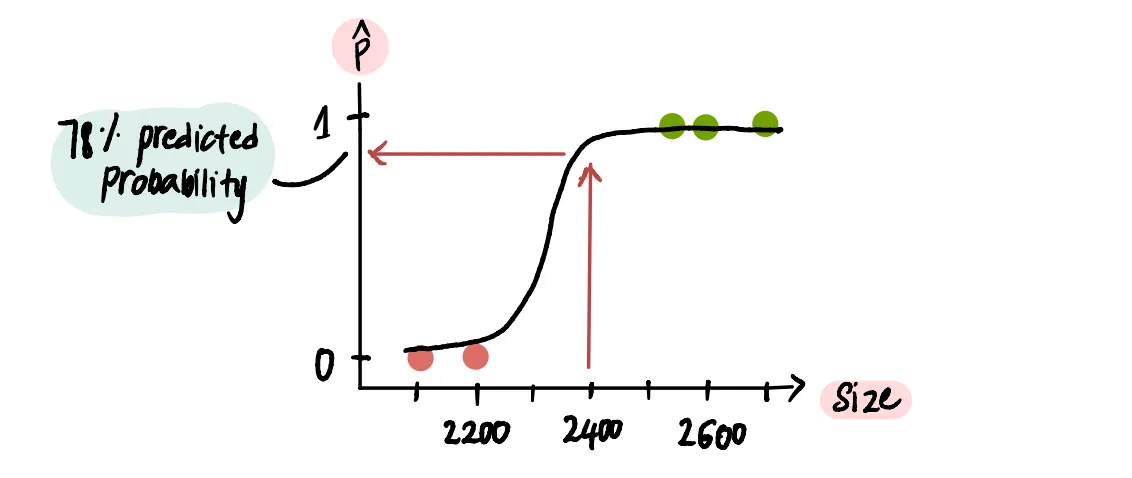
...прогнозируемая вероятность составляет примерно 78%. Таким образом, мы можем сказать Марку, чтобы он не беспокоился, потому что, похоже, вероятность продажи его дома достаточно высока.
Мы можем усовершенствовать наш подход, разработав алгоритм классификации. Алгоритм классификации обычно используется в машинном обучении для распределения данных по категориям. В нашем случае у нас есть две категории: дома, которые будут продаваться, и дома, которые не будут продаваться.
Чтобы разработать алгоритм классификации, нам нужно определить пороговое значение вероятности. Это пороговое значение вероятности разделяет предсказанные вероятности на две категории: "да, дом будет продан" и "нет, дом не будет продан". Обычно в качестве порогового значения используется 50% (или 0,5).
threshold probability value – пороговое значение вероятности
Если предсказанная вероятность для размера дома выше 50%, он будет классифицирован как "будет продан", а если ниже 50%, то как "не будет продан".
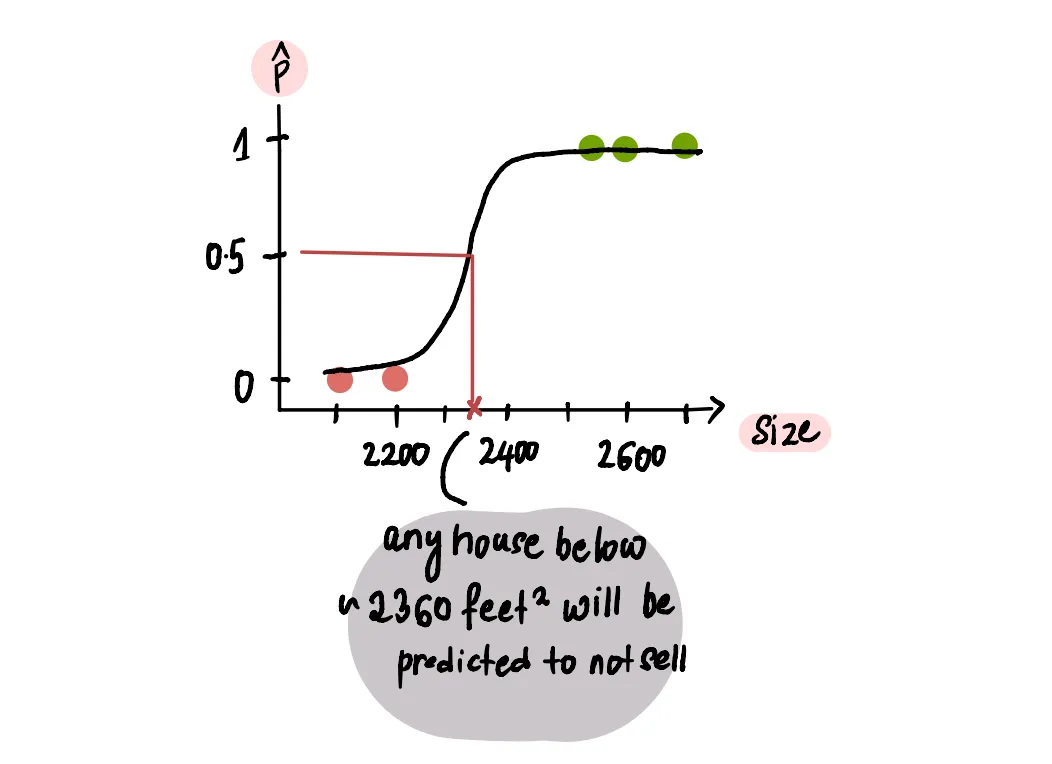
И это все. Вот как мы можем использовать логистическую регрессию для решения нашей проблемы. Теперь давайте разберемся в функции, которую мы использовали для поиска оптимальных значений для логистической регрессии.
Целевая функция
В линейной регрессии мы считаем то, насколько далеко отстояла линия от наших точек данных. А в логистической регрессии целевая функция зависит от того, насколько наши прогнозы отличаются от фактических данных, учитывая, что мы имеем дело с вероятностями.
Если бы мы использовали целевой функции MSE (как в линейной регрессии) в логистической регрессии, то в итоге получили бы невыпуклую кривую функции, с которой трудно работать.
Все дело в том, что тут будет много локальных минимумов и градиентный спуск тут будет неэффективен.
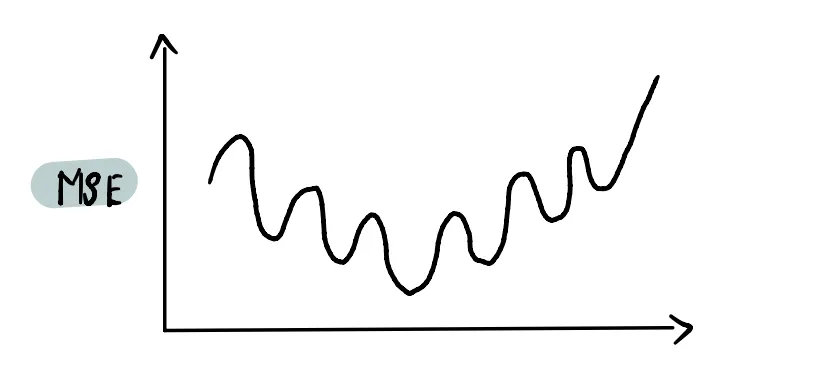
Чтобы получить выпуклую кривую функции, мы используем функцию под названием Log Loss.
Чтобы разбить функцию Log Loss, нам нужно определить отдельные затраты для случаев, когда дом действительно продан (y=1) и когда он не продан (y=0).
Дальше начинаются трудности перевода) Целевая функция на английском носит название Cost Function. Функция затрат, если переводить дословно. И вот затратами тут считаются ошибки, которые мы допускаем. Штрафом далее будем считать вклад в накопленную ошибку.
Если y = 1 и мы предсказали 1 (т.е. вероятность продажи 100%), то штраф отсутствует. Однако, если мы предсказали 0 (т.е. 0% вероятности того, что дом не будет продан), то мы получим большие штрафные санкции.
Итак, разбиваем на два случая, как и говорилось ранее.
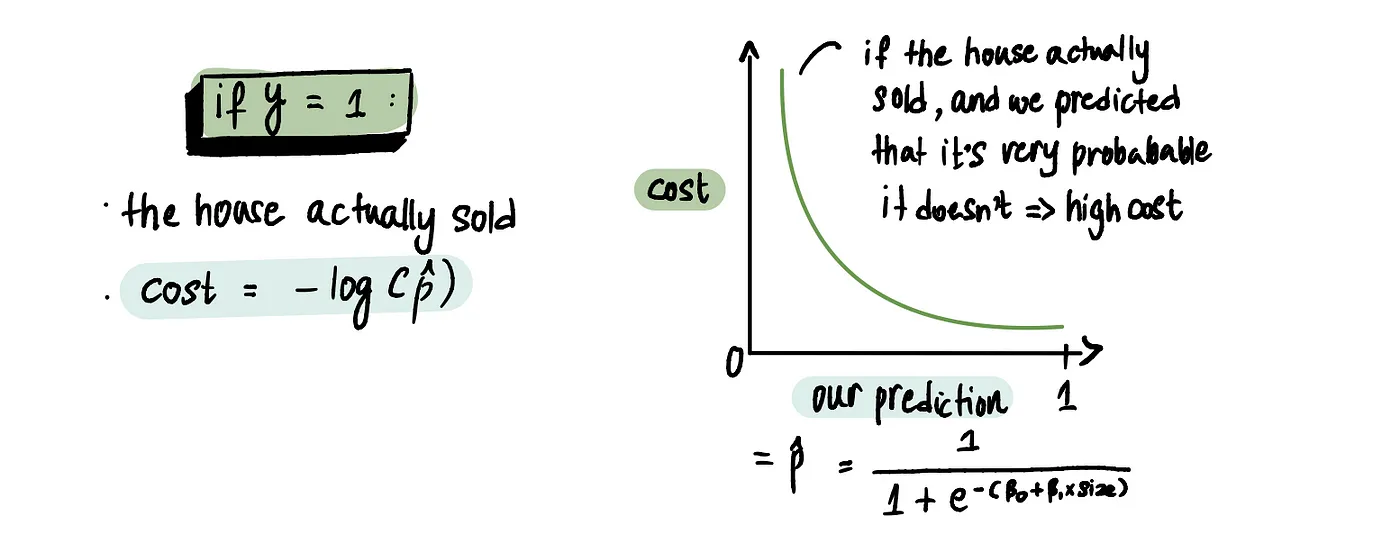
Соответственно, если мы предсказали, что дом не продастся, то есть p около нуля, то нам прилетит огромнейшая ошибка, так как логарифм улетает в бесконечность
Изменим целевую функцию для случая, когда дом не продался
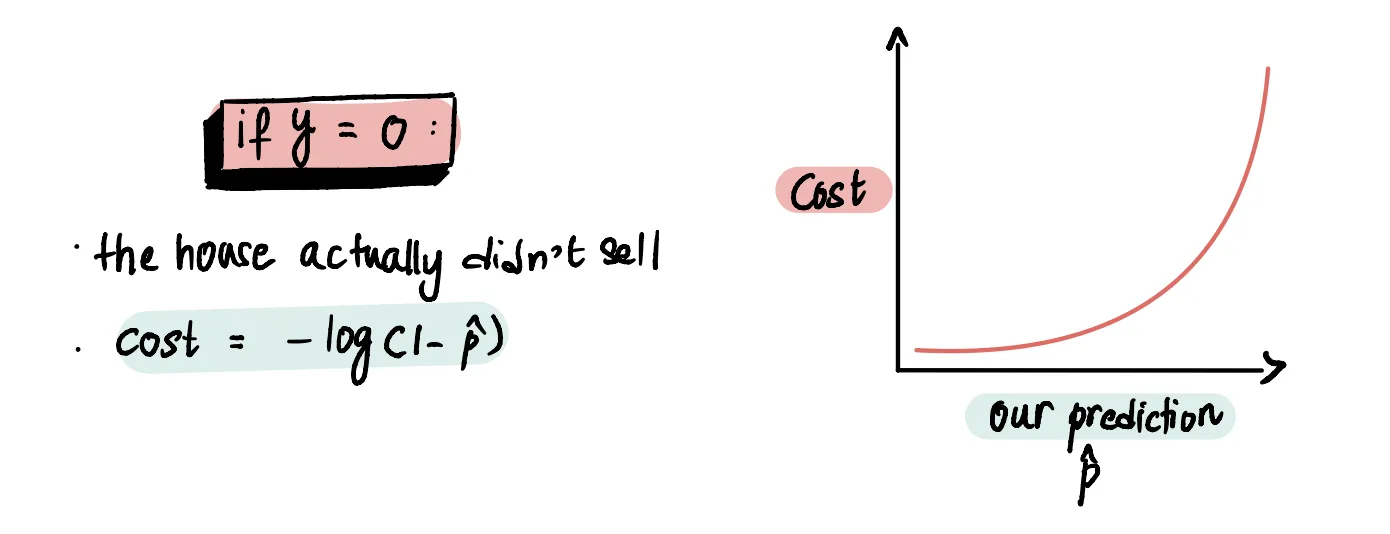
Чтобы посчитать итоговую ошибку, нужно всего лишь)
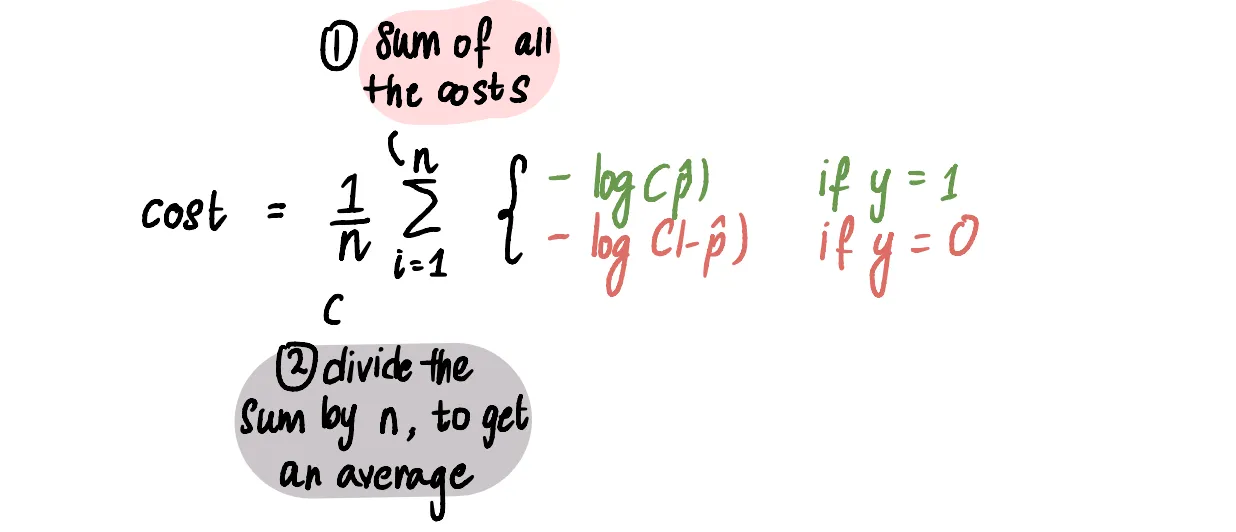
Можем даже записать это в виде одной функции
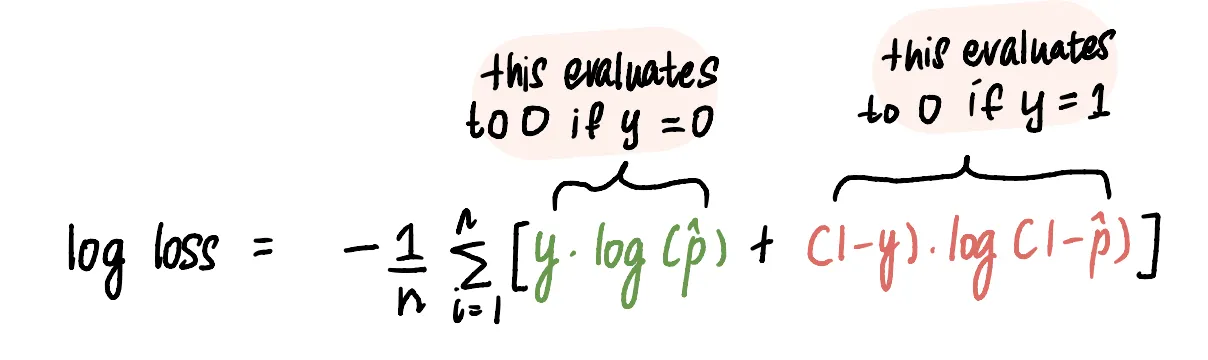
Это работает потому, что один из этих двух показателей всегда будет равен нулю, поэтому будет использоваться только второй.
И график комбинированный график выглядит следующим образом:
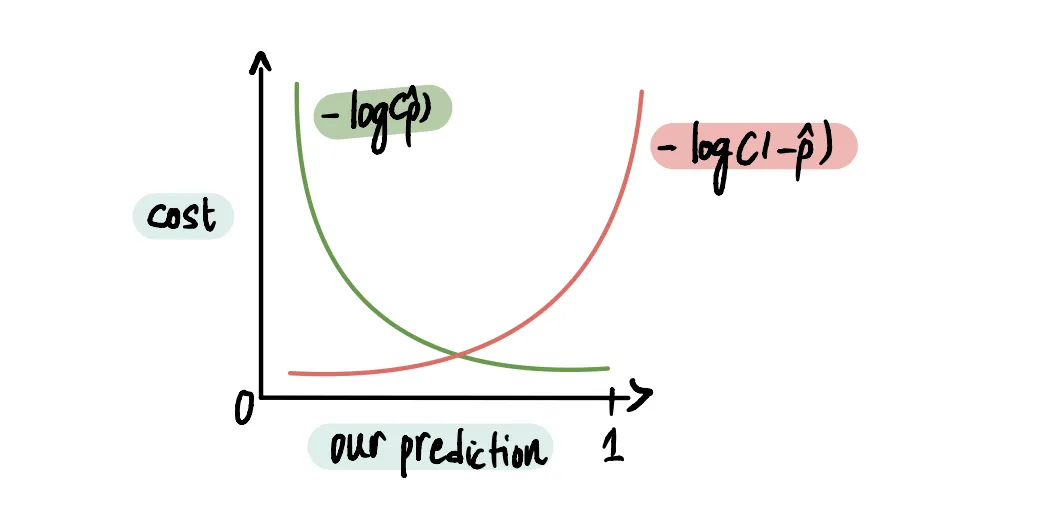
В телеграфе ужасные блоки кода, поэтому код из статьи вставлять я не буду, но знайте, что в оригинале статьи он есть и его можно оттуда позаимствовать.
На сим у меня на сегодня все. Цикл этих замечательных и подробных статей закончен. Буду послеживать за публикациями автора, мне нравится его стиль написания, особенно в этой статье, где он, как в первых двух, не опускался до каких-то ну прям очень тривиальных вещей.
Если у вас есть какие-то интересные статьи для перевода и вы считаете, что с ними было бы здорово ознакомиться, буду рад, если пришлете ссылочку.