Вектор Шепли (с иллюстрациями)
Впервые о векторе Шепли я услышал в 22 году на Матемаркетинге, там докладчик рассказывал о том, как они используют его для подсчета Value продукта. На самом деле, моделей атрибуций достаточно много и у всех есть свои плюсы и недостатки. Какие-то из них учитывают другие каналы, какие-то нет. Сегодня мы поговорим о модели, которая учитывает их, но чтобы построить такую модель у себя вам нужна слаженная работа продуктовых команд разных каналов коммуникаций с клиентами, у вас должна быть единая прометка креативов, единая логика хранения информации, иначе никак. Ну или вам повезло, и у вас какая-нибудь гугл аналитика или яндекс метрика, которая посчитает всё за вас. Таких людей тоже уважаем, но смотрим на них с осуждением)
Оригинал статьи https://medium.com/@shreya.rao/economics-illustrated-shapley-values-7d33df43ada8
Переведено для канала https://t.me/letsdatanow
Вектор Шепли - это широко используемая концепция в теории игр, которая обеспечивает справедливый способ распределения общего выигрыша в кооперативной игре между игроками. Введенная Ллойдом Шепли в 1953 году, концепция основана на идее, что каждый игрок должен получать компенсацию за свой предельный вклад в игру.
По сути, ценности Шепли помогают ответить на вопрос: насколько важен каждый игрок для общего сотрудничества, и, следовательно, на какой выигрыш может рассчитывать каждый игрок?
Давайте рассмотрим пример, чтобы понять математическую основу этих значений.
Математика, лежащая в основе Вектора Шепли
Предположим, у нас есть кооперативная игра с четырьмя игроками: Алиса, Боб, Купер и Диана.

Они решили объединить усилия и играть в игру вместе, как коалиция. Они выиграли в общей сложности $1000.

Теперь перед игроками стоит задача справедливо разделить между собой призовой фонд в 1000 долларов. Чтобы определить долю каждого игрока, нам нужно рассчитать их индивидуальные значения Шепли, которые измеряют их вклад в общий призовой фонд.
Для того чтобы определить долю каждого игрока в выигрыше, нам необходимо рассчитать их индивидуальные значения Шепли (вектор Шепли) - показатель их вклада в общий призовой фонд.
Чтобы рассчитать значения Шепли, нам также нужно знать, сколько бы выиграл каждый игрок, если бы играл индивидуально (предположим, что у нас есть эта информация). Вот индивидуальные суммы, которые выиграли бы Алиса, Боб, Купер и Диана:
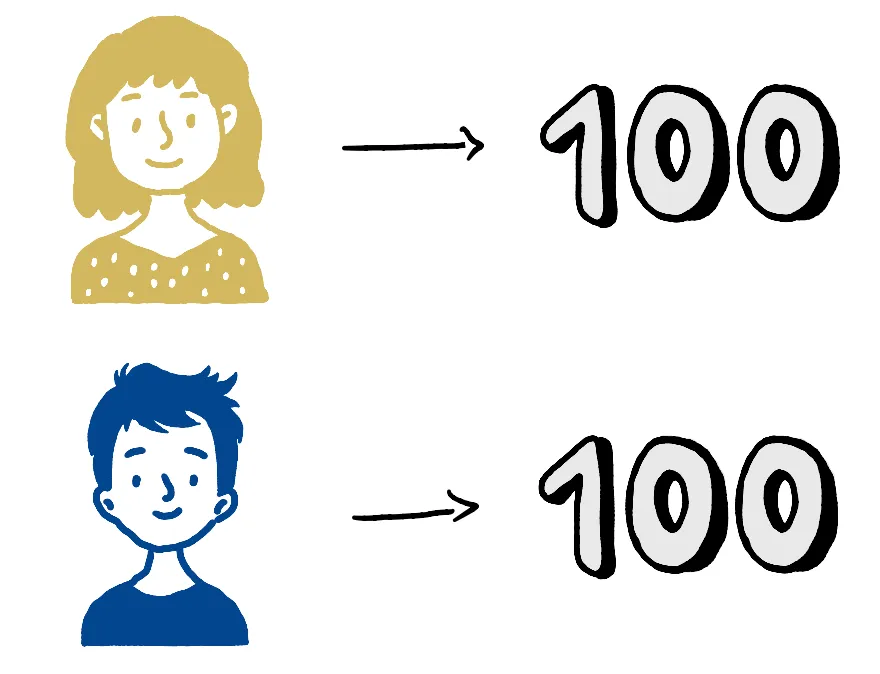
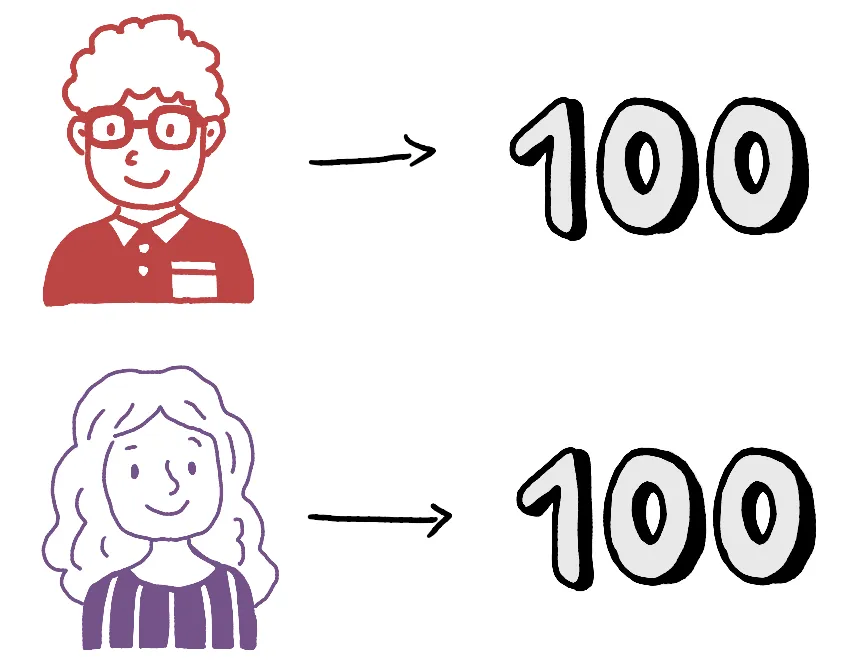
Хотя может показаться, что индивидуальные очки, заработанные каждым игроком, отражают их вклад в общий приз, это не обязательно так. Все это по той причине, что когда игроки образуют коалиции из 2 или 3 человек, они могут внести разный вклад и выиграть разные суммы призов. Чтобы учесть это, нам нужно рассмотреть сумму, которую выиграла бы каждая пара игроков, если бы они объединились и сформировали коалиции по 2.
contribution – вклад


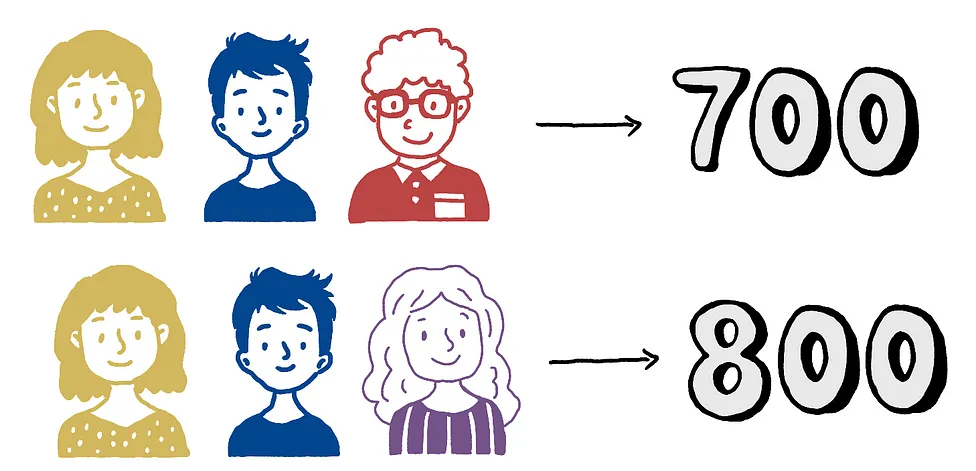
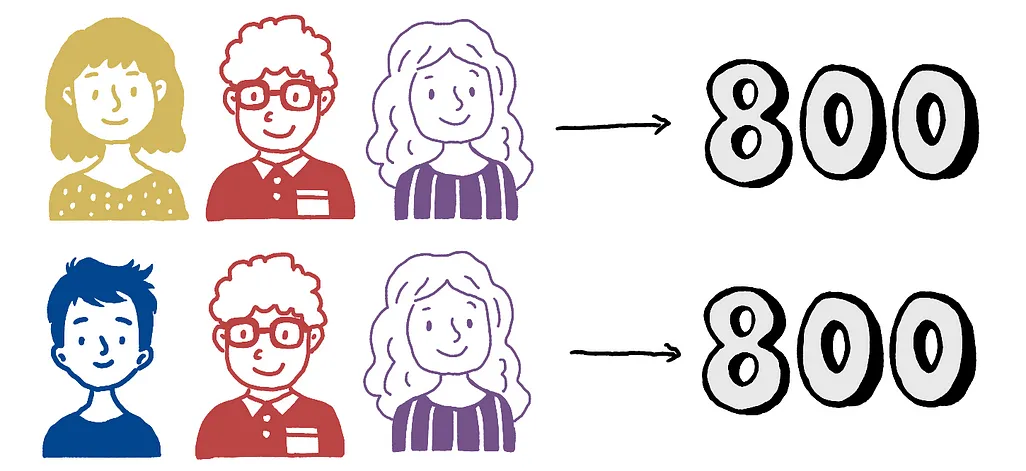
И очевидно, что если никто не играет, то денег не будет выиграно, т.е. коалиция размера 0 выиграет $0.
Теперь, когда у нас есть индивидуальные и командные вклады, мы можем вычислить значение Шепли для каждого игрока, чтобы определить его справедливую долю в призовом фонде. Давайте начнем с расчета вклада Алисы, выполнив следующие шаги:
Шаг 1: Найти коалиции, сформированные без Алисы
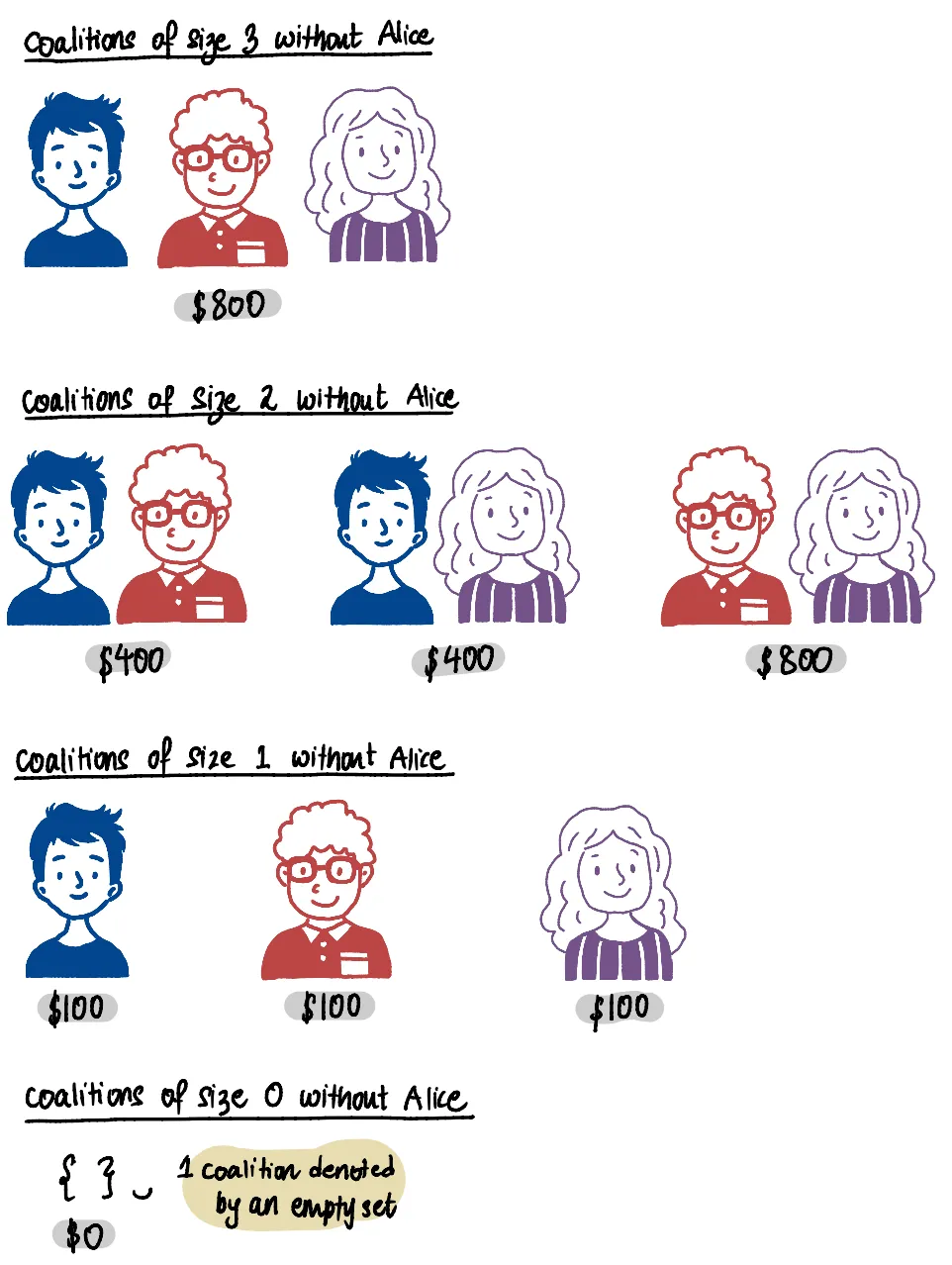
Шаг 2: Подсчитайте количество коалиций, сформированных для каждого размера коалиции
В данном случае, поскольку у нас всего четыре игрока, подсчитать количество коалиций каждого размера относительно просто. Однако для более крупных игр, скажем, со 100 игроками, эта задача становится значительно сложнее. К счастью, в теории вероятностей существует простая формула, формула комбинации для вычисления этих значений.

Например, если мы хотим найти количество коалиций размера 2, которые исключают Алису, мы знаем, что нам нужно выбрать двух игроков из оставшихся трех (Боб, Купер и Диана).
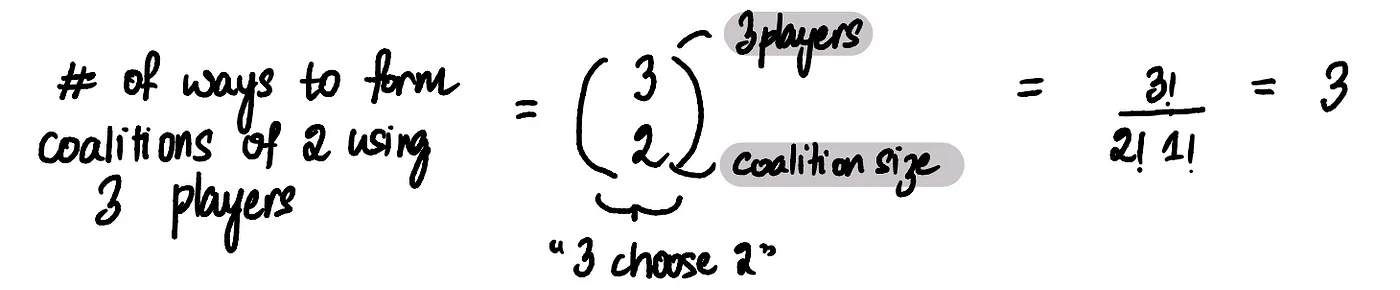
Те самые три коалиции

Также найдем количество коалиций из трех людей.
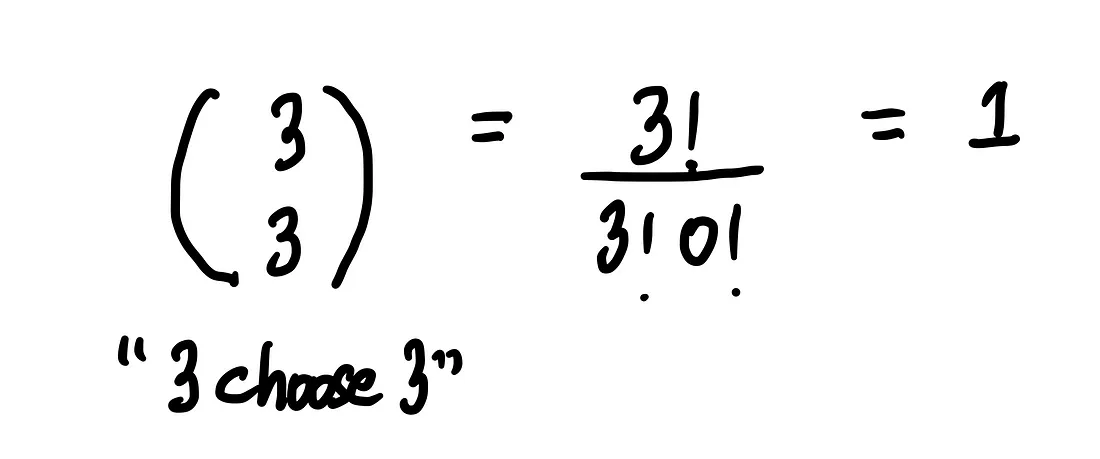

... и число способов собрать коалицию из нуля:
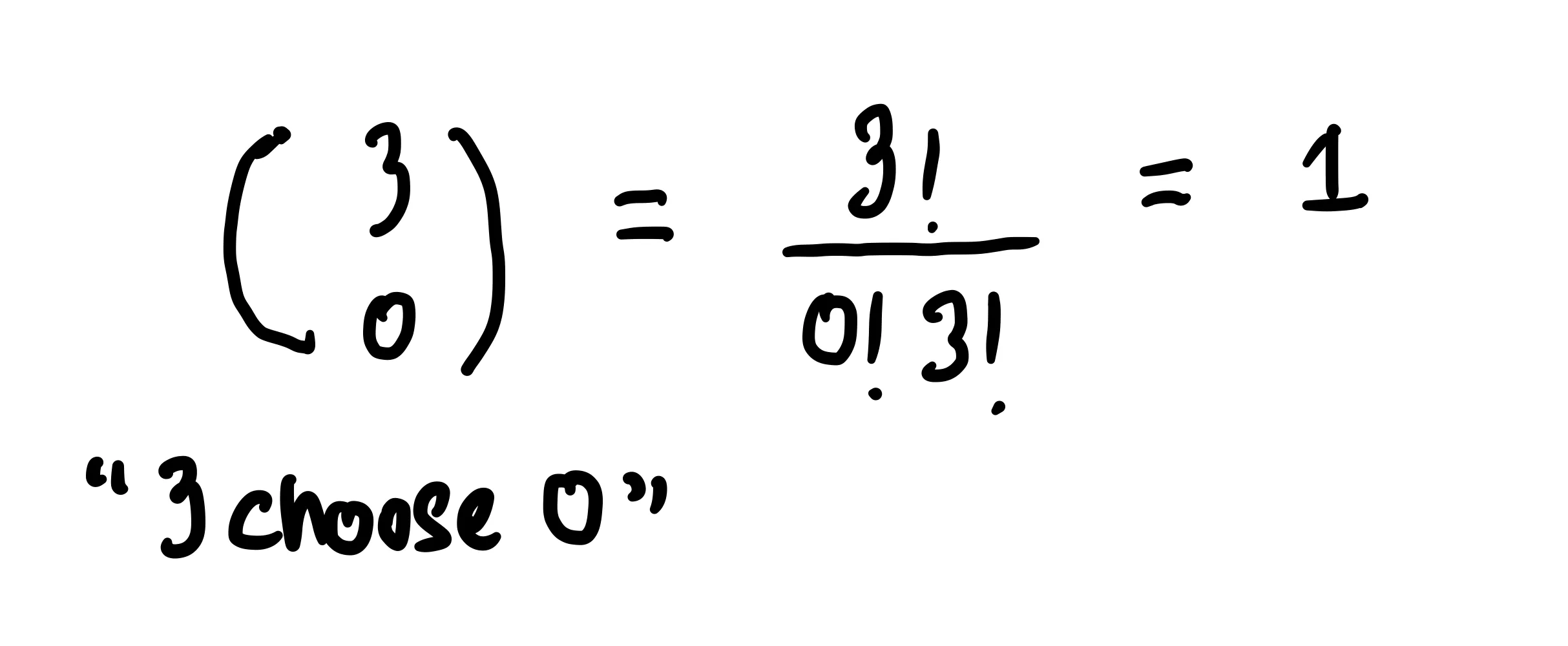
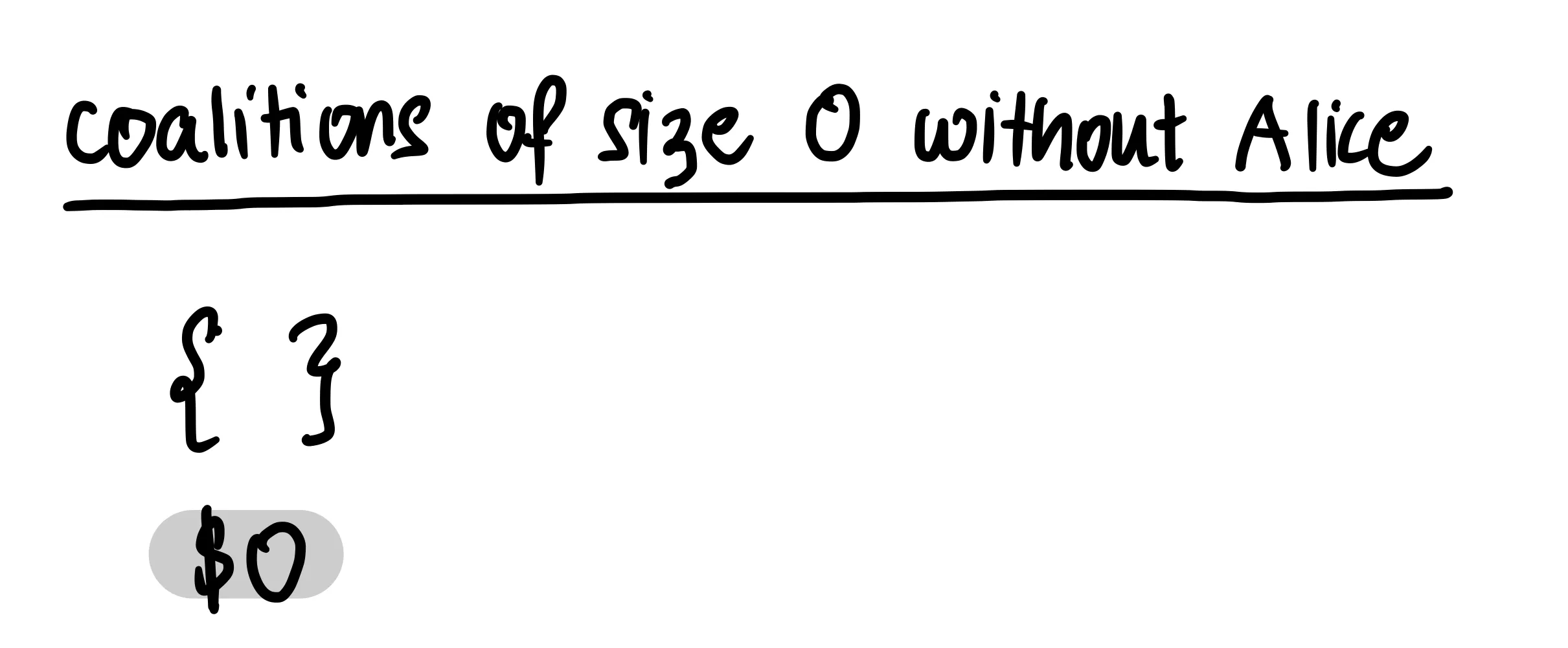
Шаг 3: Найдите средний вклад Алисы в каждую коалицию, в которую она не входит, для каждого размера коалиции.
Вклад - это дополнительная сумма призовых денег, которую Алиса приносит коалиции по сравнению с коалицией без Алисы.
Давайте начнем с нахождения среднего вклада для коалиций размера 2.

Во-первых, мы должны вычислить разницу в призовом фонде между коалицией без Алисы и призовым фондом после добавления Алисы в коалицию.
Во-вторых, мы складываем все разницы и делим эту сумму на общее количество коалиций размера 2. Это дает нам средний вклад для коалиций размера 2.
Например, рассмотрим первую коалицию размера 2 - Боб и Купер.

Без Алисы выигрыш 400, а с ней...

Получаем разницу в 300 долларов.
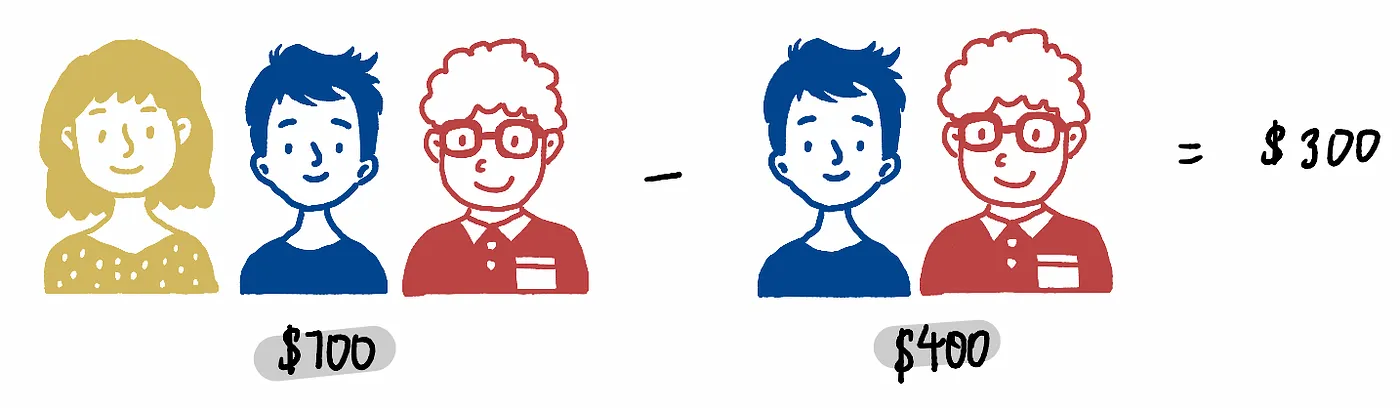
Таким образом, мы видим, что добавление Алисы в эту коалицию увеличивает ее стоимость на $300, и это считается вкладом Алисы.
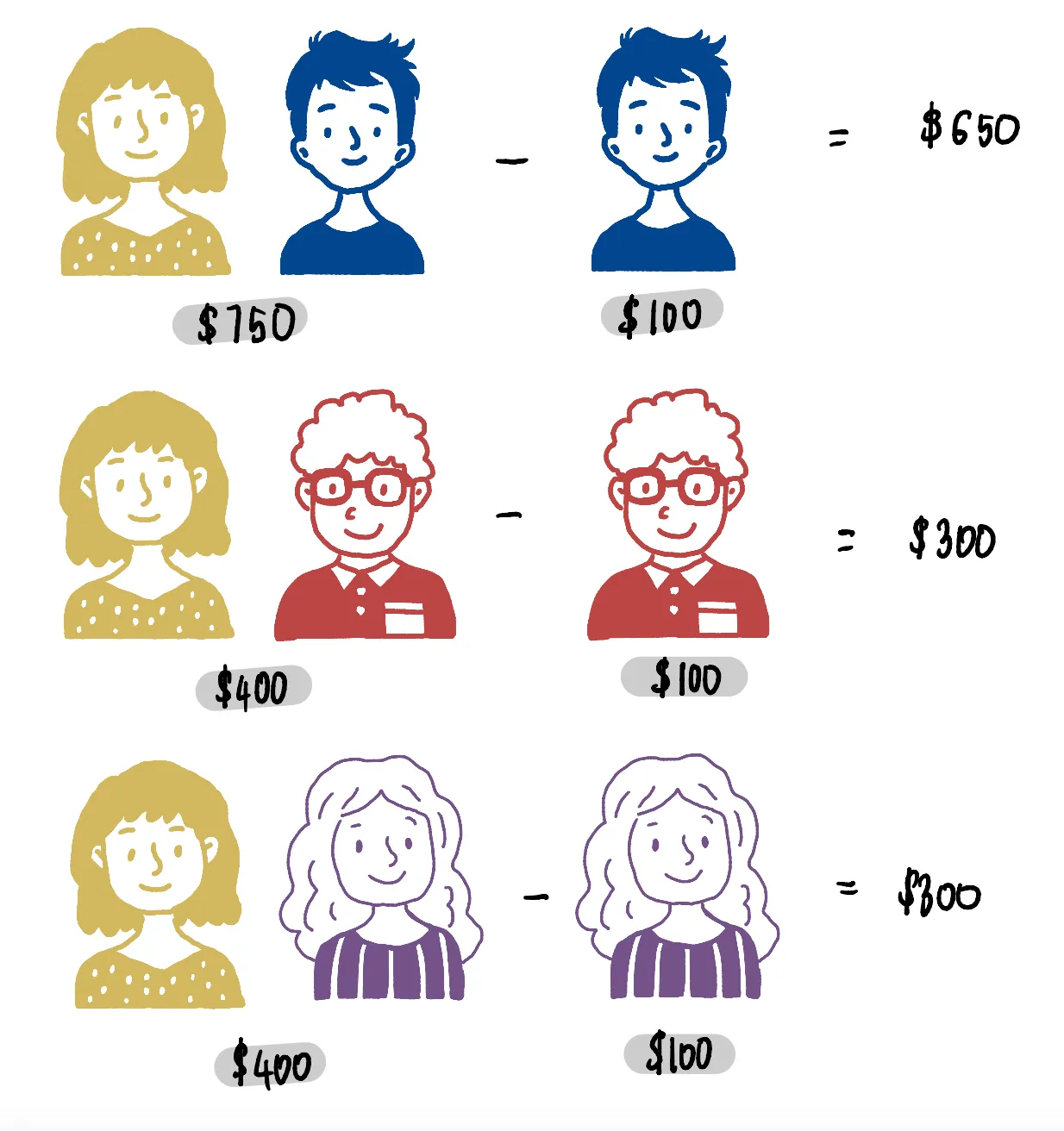
Аналогично для других коалиций размера 2:
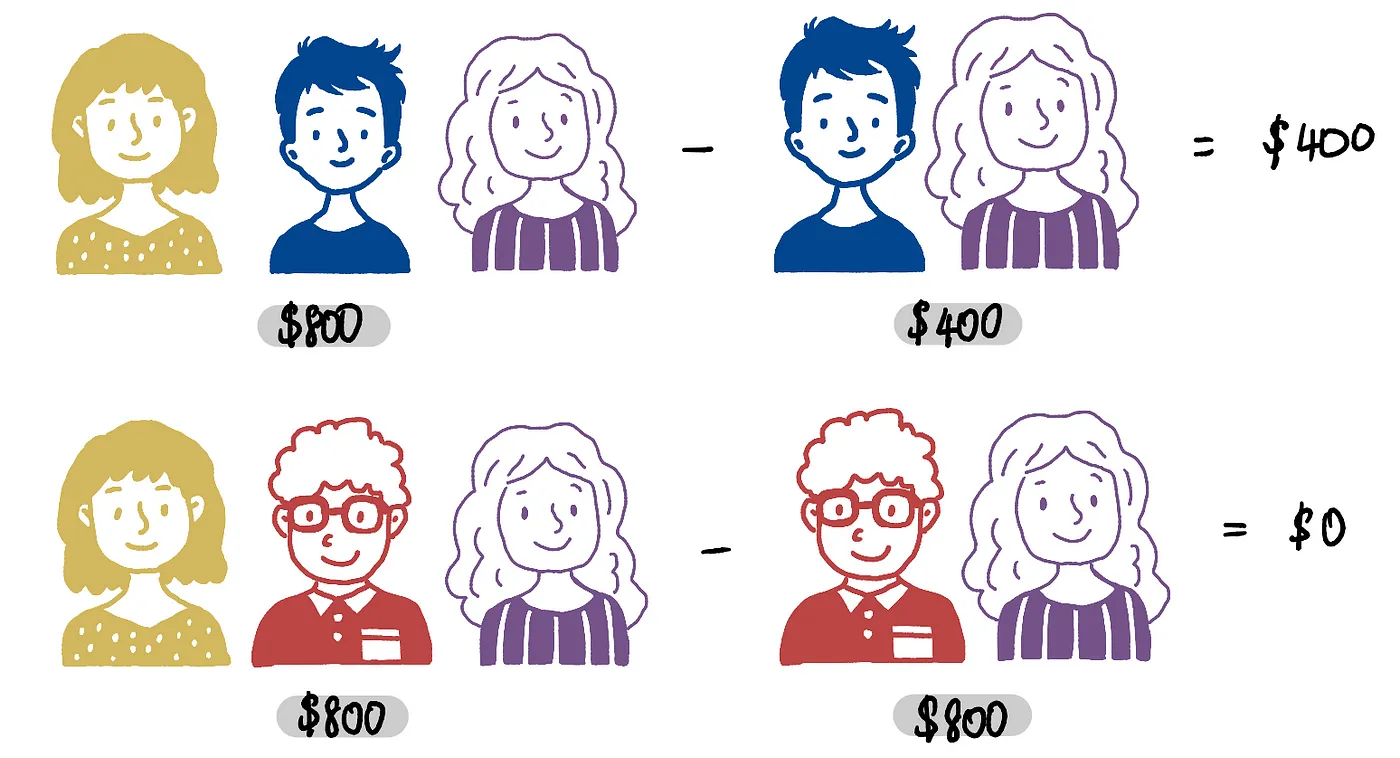
Посчитаем среднее
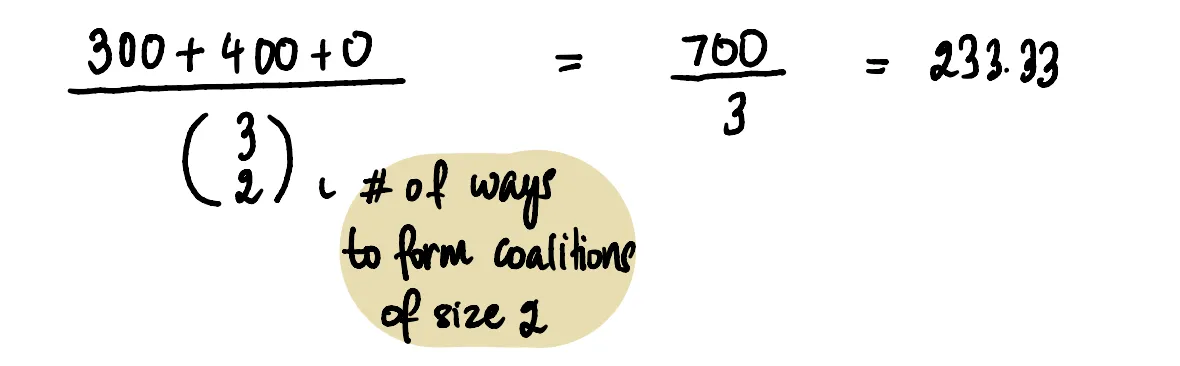
Это можно интерпретировать так: в среднем Алиса вносит вклад в $233,33, когда добавляется в коалиции размера 2.
Мы делаем то же самое для коалиций размера 3. Поскольку существует только одна коалиция размера 3, мы находим разницу в призовом фонде, когда Алиса присоединяется к коалиции:
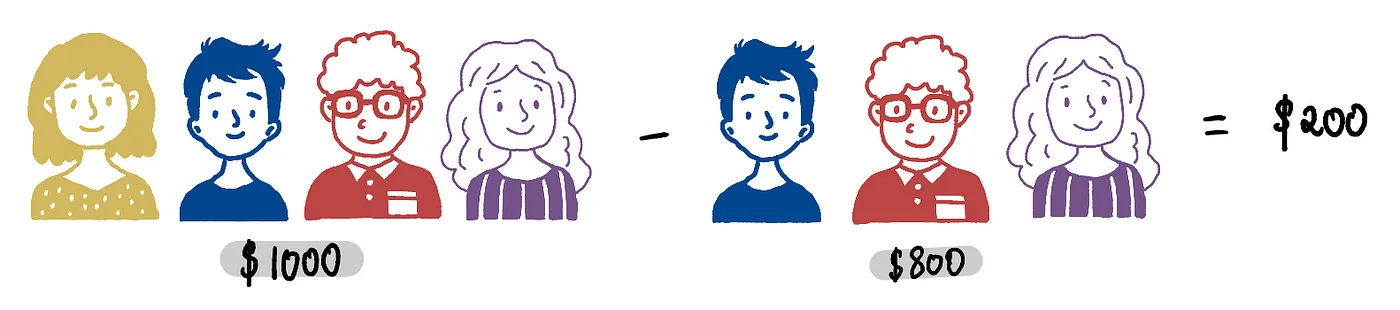
Среднее соответственно 200
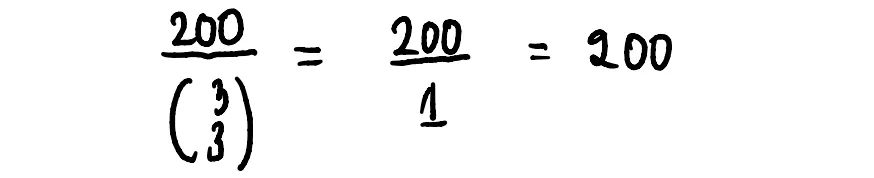
Для коалиций размера 1
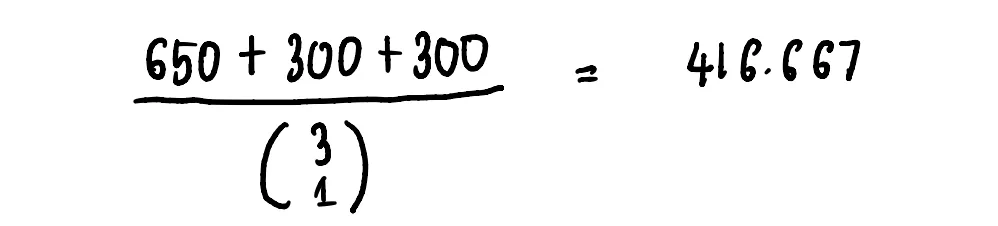
Для коалиции размера 0
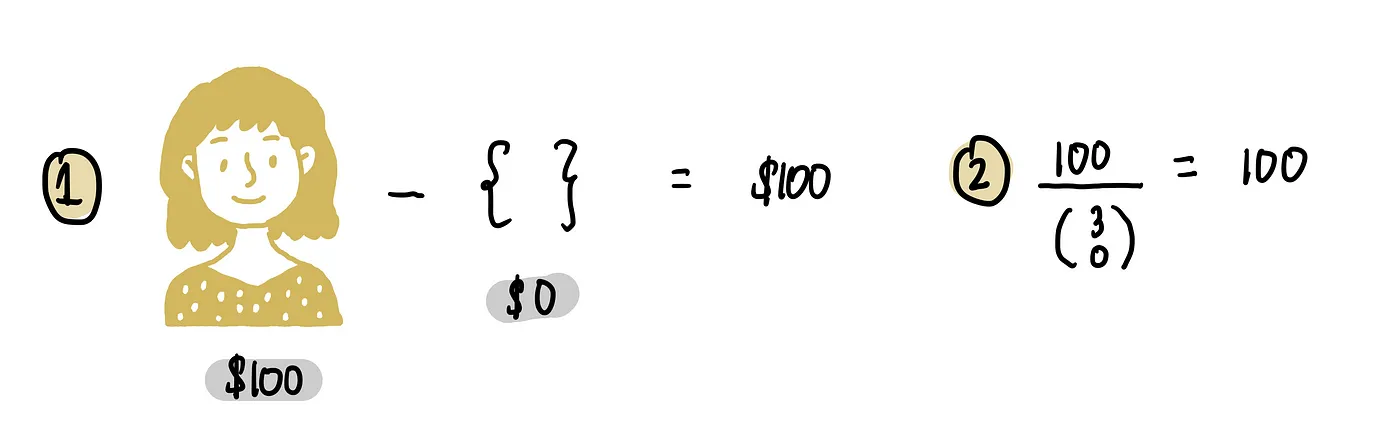
Шаг 4: Вычислить ценность Алисы по Шепли
Чтобы вычислить значение Шепли, мы складываем все средние вклады от различных размеров коалиций и делим на количество различных размеров коалиций, исключая Алису.
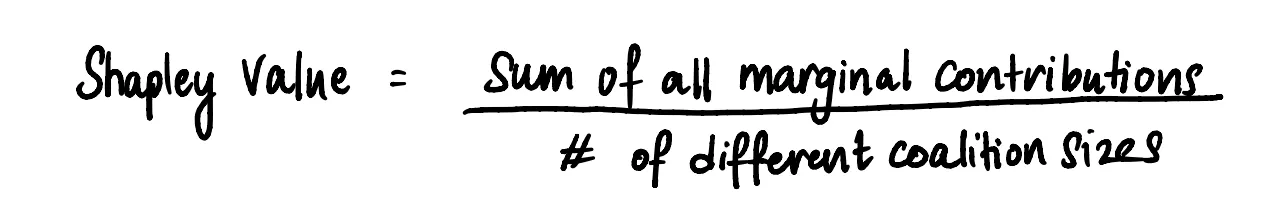
Разных размеров у нас 4 – 0,1,2,3.
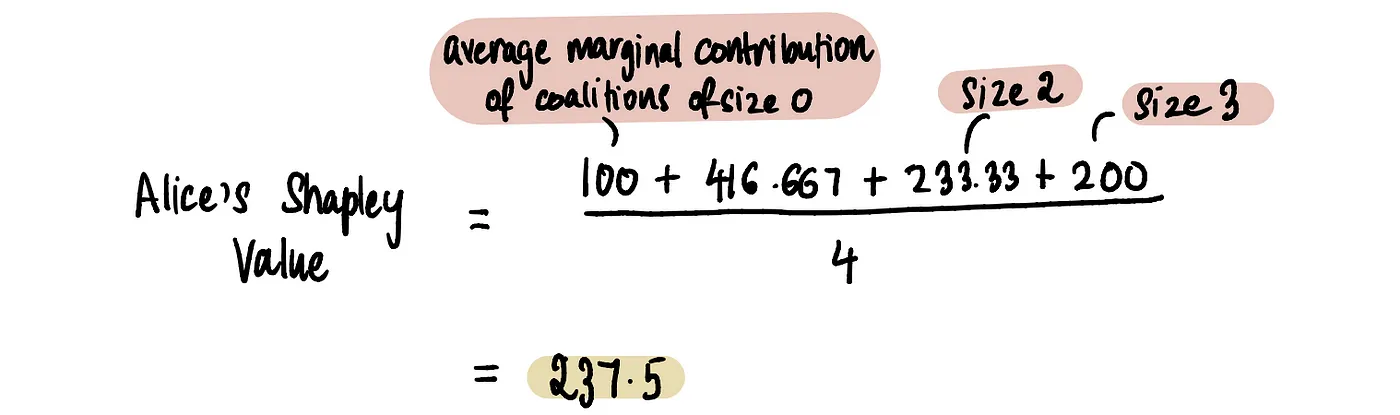
Таким образом, Алиса внесла $237,5 в призовой фонд $1000.
Посчитаем числа для остальных
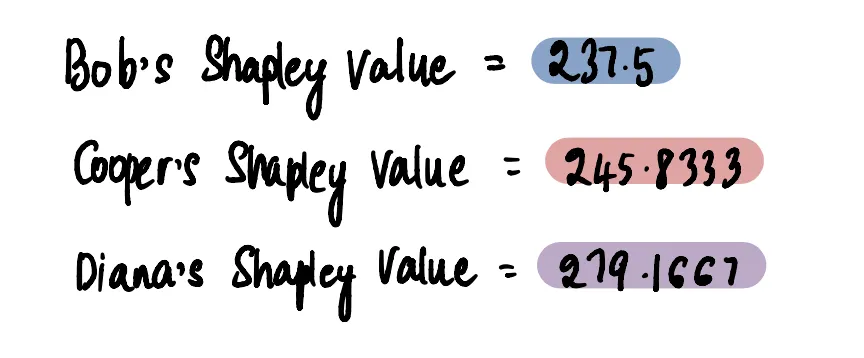
И если мы сложим их, то увидим, что 237,5 + 237,5 + 245,8333 + 279,1667 = $1000, что равно выигранному призу. Эти значения Шепли являются справедливым распределением вкладов игроков и, в свою очередь, денег, которые каждый из них получает.
ПРИМЕЧАНИЕ: Формальная формула для расчета значений Шапли такова:

В последние годы они стали популярны в машинном обучении для интерпретации моделей, особенно моделей "черного ящика", которые трудно интерпретировать.
На этом у меня сегодня все, мы уже переводили текста от этого автора и они славятся простотой английского, по этой причине сегодня всего одно слово.
Всем спасибо за прочтение, до новых встреч!