В поисках справедливости — 4. Нуклеолус
В Вавилонском Талмуде (составлен в 4 в.) приведён такой пример:
Умирает муж, у которого остаются три вдовы (в те далёкие времена у евреев было разрешено многожёнство). С каждой из жён у него был заключён брачный договор, в котором среди прочего прописано, сколько зуз (тогдашняя денежная единица) полагается выделить вдове в случае смерти мужа:
первая жена должна получить 100 зуз, вторая — 200 зуз, третья — 300 зуз.
Но что делать, если наследство меньше, чем сумма претензий всех вдов?
Талмуд предлагает решить проблему так:

Рассмотрены три случая с разным размером наследства: 100, 200 и 300 зуз. В первом случае предлагается делить между всеми поровну, в третьем — пропорционально, а во втором, казалось бы, совсем нелогичным образом. Тут важно понимать, что Талмуд — это сборник use cases, по которым должно быть понятно, как поступать в аналогичных ситуациях.
На протяжении веков читателей Талмуда мучил вопрос: по какому правилу решается эта задача?
И только в 1995 г. Роберт Ауманн (лауреат Нобелевской премии по экономике 2005 г.) разгадал это правило. Им оказался нуклеолус — концепция, разработанная другим израильским экономистом Дэвидом Шмейдлером в 1969 г.
Разберём идею нуклеолуса на примере задач, решённых в предыдущей заметке методами ядра и вектора Шепли.
Задача 1. Три одинаковых по размеру коттеджных посёлка (1-й — А, 2-й — Б и 3-й — В) расположены вдоль одной просёлочной дороги на расстоянии соответственно 6, 18 и 36 км от автотрассы. Принято решение заасфальтировать просёлочную дорогу. Цена 1 км дорожных работ составляет 1 ₽. Как посёлки должны поделить расходы на строительство дороги?
Решение. В прошлый раз мы нашли для этой задачи вектор Шепли x = (2; 8; 26).
Основной посыл нуклеолуса (дословно: ядрышка) состоит в следующем. Нужно взять группу наименее довольных дележом и попытаться максимизировать их выигрыши (удовольствия) за счёт тех групп, кто получил от дележа большой выигрыш.
В качестве величины удовольствия (выигрыша) ∆x предлагается взять разность между той платой, которую нужно было бы внести, если бы пришлось строить дорогу самостоятельно, и той, уменьшенной за счёт кооперативного эффекта платой, которая определена вектором Шепли.
Рассчитаем удовольствия для каждого отдельного игрока и каждой коалиции игроков и внесём их в таблицу:

Наименьшее удовольствие — 0 — имеет коалиция, состоящая из всех трёх игроков; но его увеличить, очевидно, невозможно: нет того игрока, за счёт которого это можно было бы сделать.
Следующая наименьшая величина удовольствия — 2, её имеет коалиция игроков Б и В. Все остальные — поодиночке или в парах — имеют больший показатель удовольствия от дележа расходов на строительство дороги. И, наверное можно проникнуться к ним сочувствием, эта коалиция Б-В испытывает определённую обиду от такого положения вещей. Она предлагает подправить делёж таким образом, чтобы их удовольствие увеличилось за счёт чьего-нибудь другого и в результате стало ему равным. Увеличить своё удовольствия эта коалиция может, очевидно, только за счёт игрока А. Поскольку игроки Б и В имеют одинаковые удовольствия, перекинем от них в векторе Шепли x = (2; 8; 26) по 0,5 рубля игроку А, получим новую величину y = (3; 7,5; 25,5). Для неё заполним таблицу удовольствий:

Видим, что минимальное значение удовольствия — 3 — в этой таблице увеличить уже невозможно: игрок А может поднимать его за счёт игроков Б и В, а те, в свою очередь, только за счёт А. Именно это распределение платежей y = (3; 7,5; 25,5) называют N-ядром, ядрышком, или нуклеолусом. Оно уже не обладает свойствами аддитивности (как вектор Шепли), но отвечает некоторым другим соображениям, связанным с пониманием справедливости, а именно, понятию устойчивости.

Задача 2. Три музыканта Альт, Бас и Виолончель играют в подземном переходе. Играя один, Альт зарабатывает за вечер 100 ₽, Бас — 200 ₽, Виолончель — 1000 ₽. Если они играют парами, то Альт и Бас собирают 400 ₽, Альт и Виолончель — 1300 ₽, Бас и Виолончель — 1500 ₽. Они вышли втроём и заработали 2200 ₽. Как им поделить эти деньги?
Решение. Вектор Шепли был найден ранее, он равен x = (350; 500; 1350).
Составим таблицу удовольствий игроков:
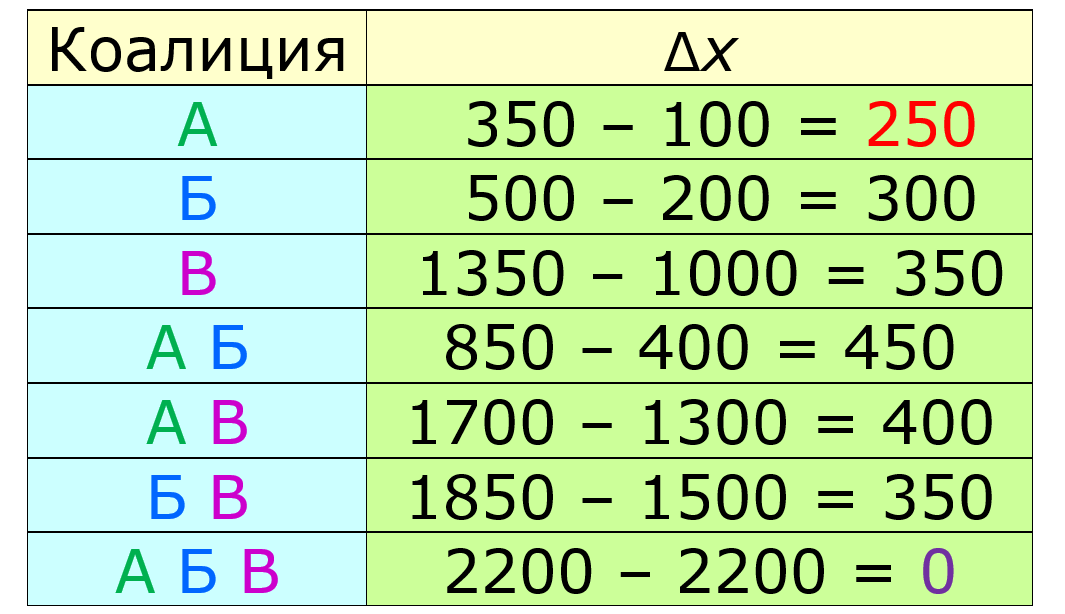
Нулевое значение удовольствия у всей коалиции не может быть улучшено. Следующее по минимальности значение у игрока А — 250. Его можно увеличить до 300 за счёт игрока В. Рассмотрим делёж y = (400; 500; 1300) и составим для него таблицу удовольствий:
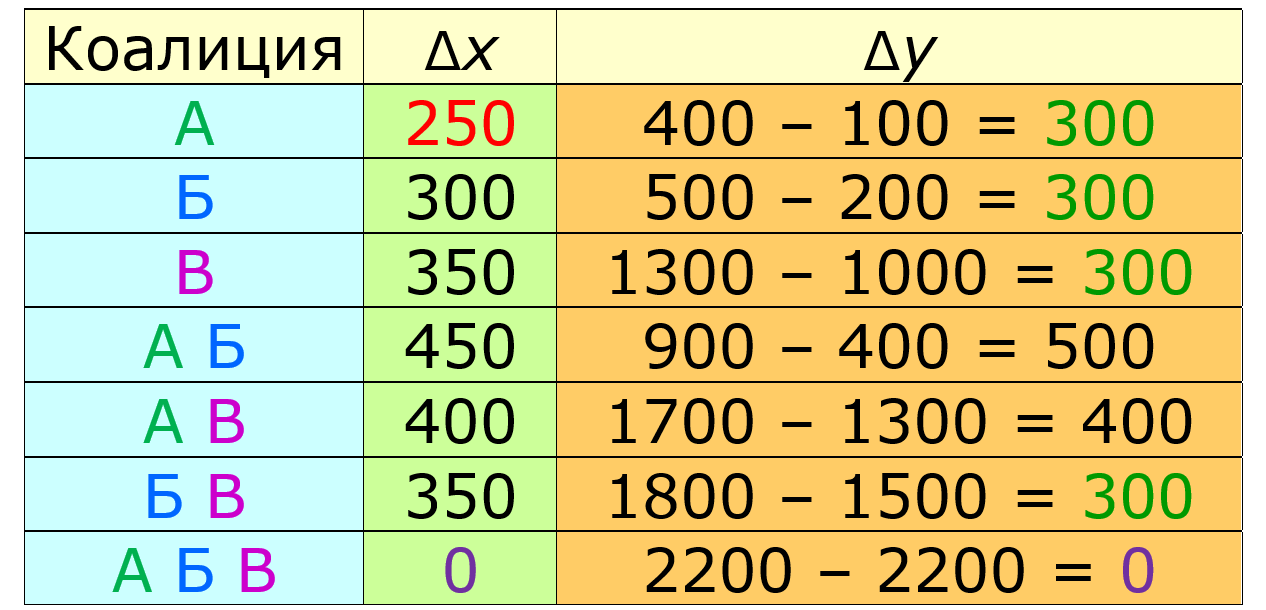
Мы получили равновесную ситуацию: у игрока А удовольствие 300, и у коалиции Б-В тоже 300, а их удовольствия могут изменяться только за счёт друг друга. Значит, найденный платёж образует нуклеолус.
При большом дисбалансе выигрышей нуклеолус несколько улучшает положение самых малоимущих относительно вектора Шепли.

Возвращаясь к задаче из Талмуда о трёх вдовах, можно сказать, что её решение совпадает с нуклеолусом. Но при этом совершенно не понятно, как таким сложным математическим аппаратом могли воспользоваться древнееврейские мыслители!
Применительно к этой задаче общие правила дележа наследства согласно концепции нуклеолуса получаются такими: если сумма требований меньше половины состояния, каждая вдова получает поровну, но не больше, чем половину того, что должна была получить; если же сумма требований больше половины состояния, то каждая сначала получает половину, а остаток делится так, что каждая недополучает поровну, но не больше своего убытка.

Именно при таком способе дележа все вдовы оказываются максимально удовлетворены, а все их убытки минимизированы.
Интересную гидравлическую аналоговую модель нуклеолуса предложил Марек Камински — в виде сообщающихся сосудов определённой конфигурации.

Высота каждого такого сосуда — это размер требований. Сосуды поделены на две части. Объём жидкости в сосудах — это размер наследства. С помощью этой гидравлической аналогии гораздо проще представить, как пару тысяч лет назад люди без современного математического аппарата могли найти такое нетривиальное решение проблемы и при этом считали его эталонным и само собой разумеющимся.
И, кстати, согласно пониманию древнееврейских мыслителей и современной концепции нуклеолуса, действующие ныне правила в области банкротства устроены несправедливо.