UniLecs #183. Игра ГО

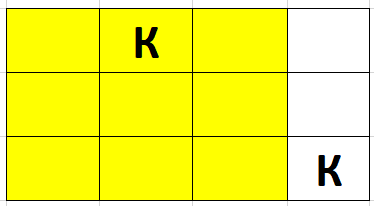
Задача: на клетчатом поле игры ГО размером NxM остались два камня. Необходимо определить максимально возможную площадь прямоугольника, которому принадлежит только один из камней. 

Входные данные: N,M - натуральные числа от 2 до 1000. Points[(x1, y1), (x2, y2)] - массив координат двух камней.

Вывод: площадь максимального прямоугольника

Пример: N = 3, M = 4;

Points = [(2, 1), (4, 3)]

Answer = 9;

Идея: у нас есть два камня на поле: K1 (x1, y1) и K2 (x2, y2) и поле NxM.

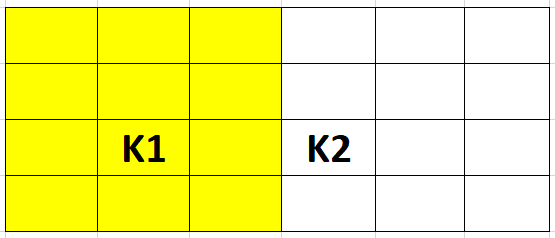
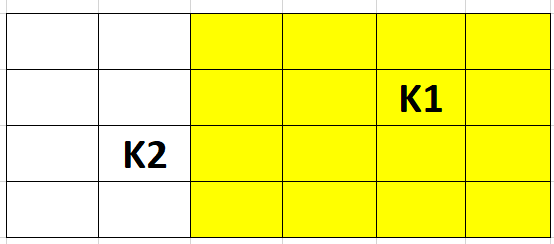
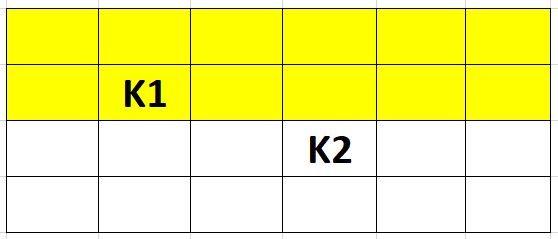
Пусть K1 принадлежит максимально возможному прямоугольнику. Тогда возможны 4 случая, рассмотрим их:

1. x1 < x2: Прямоугольник (1,1) - (x2 - 1, N).

2. x1 > x2: Прямоугольник (x2 + 1, 1) - (M, N).

3. y1 < y2: Прямоугольник (1, 1) - (M, y2 - 1).

4. y1 > y2: Прямоугольник (1, y2 + 1) - (M, N).

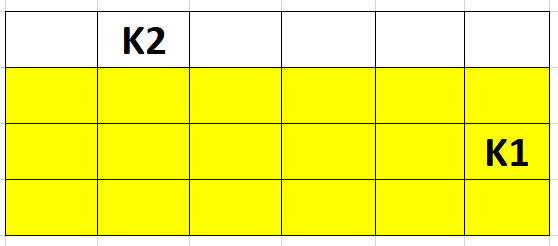
Среди всех прямоугольников выбираем с наибольшей площадью. Мы предположили, что наибольший прямоугольник возможен для 1го камня K1, но это может быть неверно. Поэтому данную процедуру нужно применить и для 2го камня K2.

Реализация:

https://gist.github.com/unilecs/52cb63f4ef3d78005970a6c8327d0cf6

Play-test: https://dotnetfiddle.net/Md9qIN