UniLecs #172. Особенные числа

Задача: выделим особый вид натуральных чисел, таких что, в своем представлении число не содержит единиц, а произведение всех его цифр равно N.

По заданному числу N необходимо определить количество всевозможных особых чисел.

Входные данные: N - натуральное число от 1 до 1000.

Вывод: количество особых чисел для N.

Пример:

1. N = 6; Answer = 3. (6, 23, 32)

2. N = 8; Answer = 4. (8, 24, 42, 222)

Идея: пусть f(N) - количество особых чисел для числа N.

Частные случаи: 

1. N = 1 => f(1) = 0. Очевидно, что нет такого числа, которые не содержит единицу в представлении и произведение цифр которого равно 1.
2. N - простое число и меньше 10, т.е. 2, 3, 5, 7.  Для этих чисел f(N) = 1, т.к. числа простые, то кроме себя, делителей у них больше нет.

По сути для определения общего случая f(N) нам нужно посмотреть все делители d (от 2 до 9, т.к. цифры в числе могут быть только от 2 до 9) заданного числа N и далее просуммировать значения f(N / d).

Для наглядности, давайте разберем конкретный пример: N = 8

1. 8 -> 2 * f(4) -> 2 * f(2) -> 2 * f(1) (Собираем делители 2 2 2 -> первое особое число = 222)
2. 8 -> 2 * f(4) -> 4 * f(1) (2 4 -> второе особое число = 24)
3. 8 -> 4 * f(2) -> 2 * f(1) (4 2 - третье особое число = 42)
4. 8 -> 8 * f(1) (8 - четвертое особое число)

Реализация:

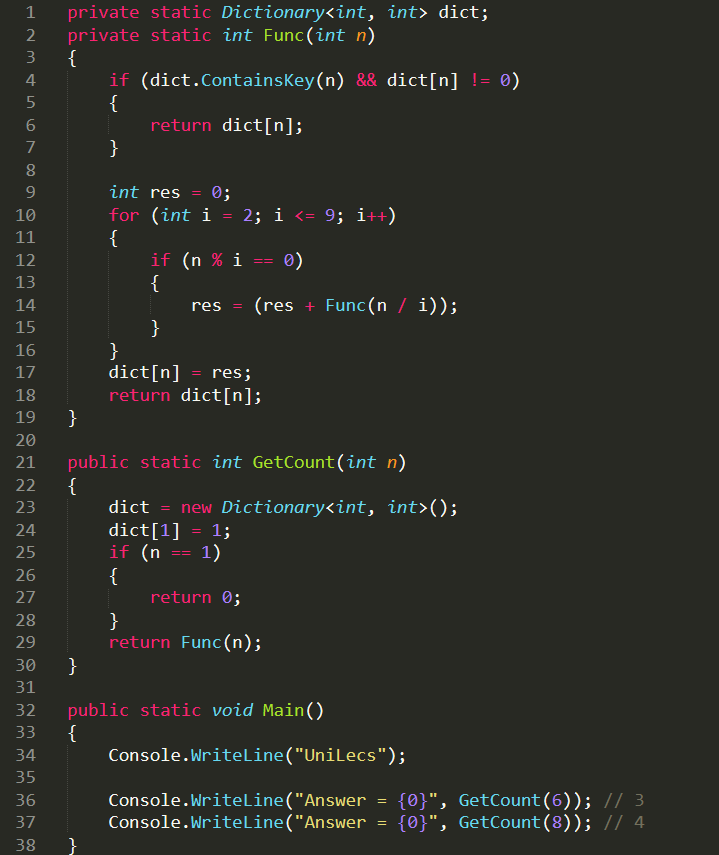
https://gist.github.com/unilecs/32107c4d301a085e2189b31251f71f27

Play-test: https://dotnetfiddle.net/RxRfU7