UniLecs #167. Правильные треугольники

Задача: задачка из старого советского журнала Квант. Дан правильный треугольник со стороной длины N, этот треугольник разбит на единичные правильные треугольники (смотри примеры). Необходимо определить сколько существует всевозможных правильных треугольников для произвольного N.

Входные данные: N - натуральное число от 1 до 10^4.

Вывод: количество всевозможных треугольников.

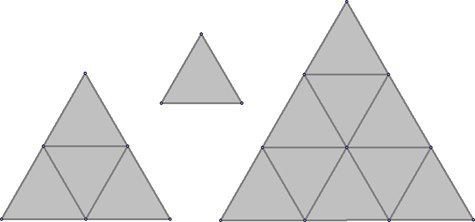
Пример:

1. N = 1; Answer = 1

2. N = 2; Answer = 5

3. N = 3; Answer = 13

Идея: давайте будем отдельно рассматривать треугольники направленные вверх и направленные вниз.

Треугольники, направленные вверх - U (up)

Кол-во треугольников со стороной n будет равно 1.

Кол-во треугольников со стороной 1 будет равно Sn, где Sn - сумма арифметической прогрессии для n. Так как очевидно, что от вершины треугольника до основания кол-во треугольников будет увеличиваться на величину арифм.прогрессии (см.рисунок).

Тогда: кол-во треугольников со стороной 2 будет равно S(n-1) и т.д.

Получаем, что кол-во всевозможных треугольников направленных вверх равно:

S = Sn + S(n-1) + S(n-2) + ... + S2 + S1

Треугольники, направленные вниз - D (down)

Очевидно, что кол-во треугольников со стороной n будет равно 0, таких треугольников нет.

Кол-во треугольников со стороной 1 будет равно S(n-1), где S(n-1) - арифмт.прогрессия для n-1 (смотри рисунок).

Кол-во треугольников со стороной 2 будет равно S(n-3)

Кол-во треугольников со стороной 3 будет равно S(n-5) и т.д.

Ответом будет общее кол-во треугольников направленных вверх и вниз.

Реализация:

https://gist.github.com/unilecs/322f6a2f6acb446b8f72f400b371e9b1

Play-test: https://dotnetfiddle.net/25Fl1h