UniLecs #141. Math Lottery
UniLecs
Задача: математики придумали свою версию лотереи. На лотерейном билете указана прямоугольная числовая матрица N*M, также есть скрытая часть, где указаны координаты ячейки X. Есть четыре возможных выигрышных направления: вверх/вниз и влево/вправо. Направление считается выигрышным, если все числа в этом направлении от ячейки X строго меньше числа в самой ячейке X. Если ячейка X находится на краю матрицы, то вы автоматически имеете выигрышное направление.
Необходимо выбрать такой лотерейный билет, ктр имеет максимальное общее кол-во выигрышных направлений для всех возможных игровых ячеек (определить только по исходной матрице, скрытая часть ест-но вам неизвестна).
Входные данные: arr - числовая матрицы N*M, эл-ты матрицы - натуральные числа от 1 до 10^3. N,M от 1 до 100.
Вывод: вывести общее кол-во выигрышных направлений для заданной таблицы.
Пример:
[ { 6, 4, 10, 11 },
{ 2, 9, 9, 3 },
{ 5, 4, 5, 4 } ]
Answer: 25

1 рис: всего 25 всевозможных выигрышных комбинаций;
2 рис: рассмотрен конкретный случай лотереи для ячейки X(2, 2).
Идея: по сути нам нам нужно обработать матрицу с каждой из сторон. Отдельной функцией нам нужно пройтись по каждой строке матрицы и посчитать кол-во ячеек, для ктр левое направление будет выигрышным. Т.е. для каждой строки необходимо определить кол-во таких элементов arr[i, j], что все элементы, стоящие в строке до него, строго меньше arr[i,j].
Осталось сделать тоже самое для каждой из сторон матрицы. Для простоты понимания просто сделаем функцию, ктр поворачивает матрицу по часовой стрелке и выполним функцию подсчета для каждой из матриц.
Рассмотрим на исходном примере:

Примечание: в данном случае, я привел решение с помощью поворота матрицы, т.к. оно наглядно показывает суть подхода. Но оно не оптимально по времени и по памяти, т.к. мы для каждой стороны исходной матрицы создаем новую матрицу поворотом.
Реализация:
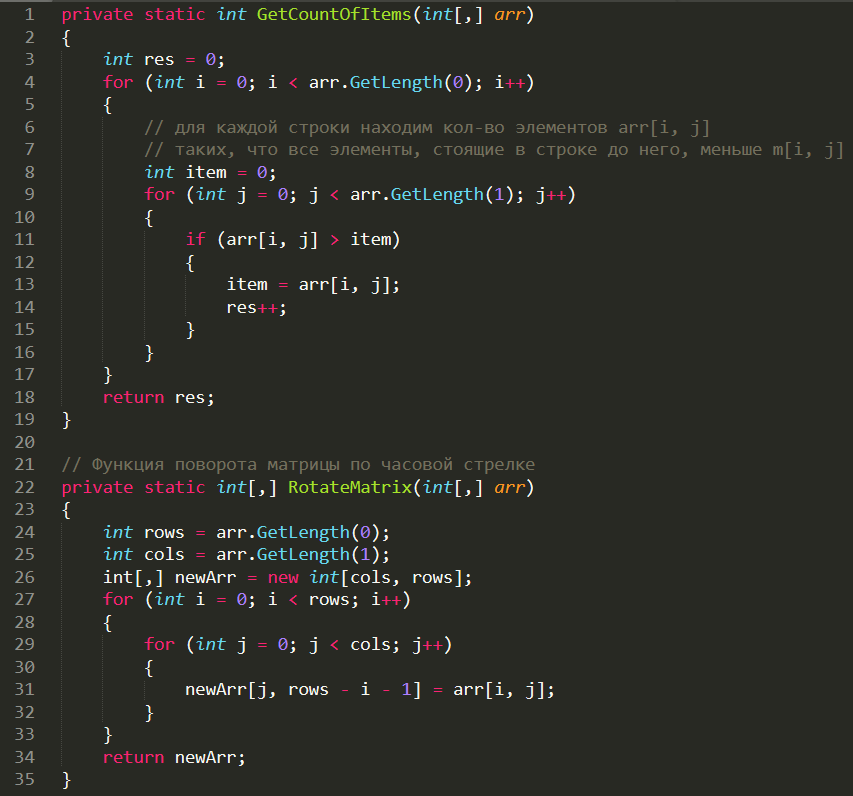
RotateMatrix - функция поворота матрицы по часово стрелке.

https://gist.github.com/unilecs/b89a540437d91dd7ff1ce294ad6f7fc3
Test: