UniLecs #137. Multiplication of digits
UniLecs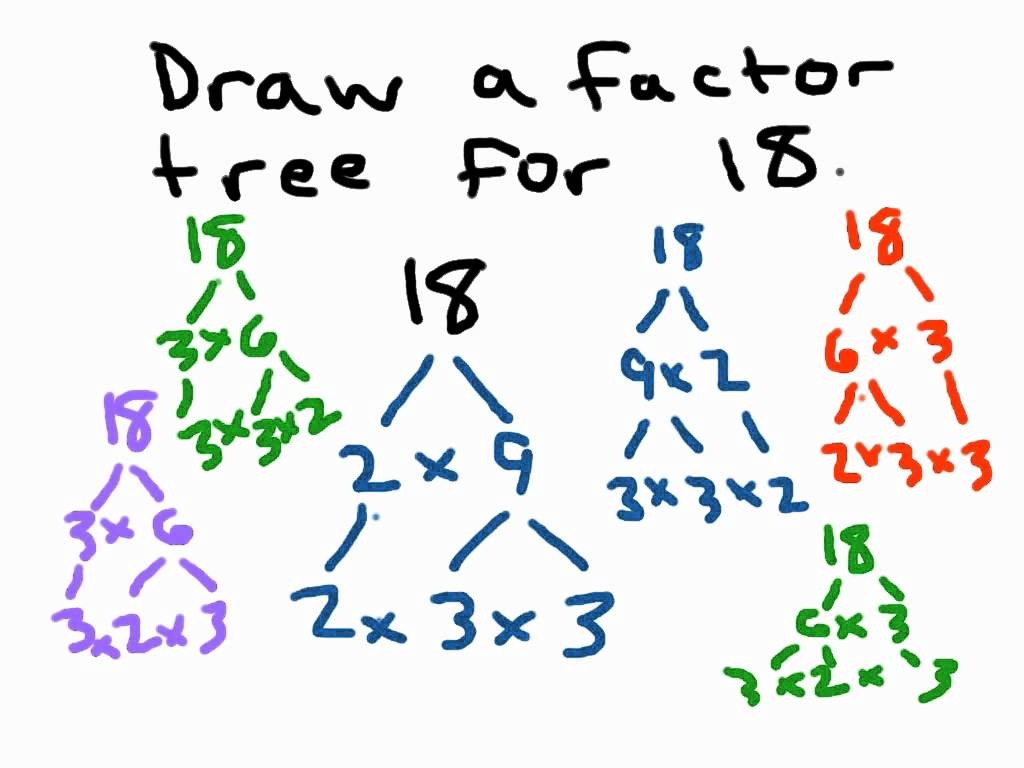
Задача: дано натуральное число N. Необходимо найти наименьшее натуральное число, в ктр произведение его цифр было бы равно N. Если такого числа не существует, вывести -1.
Входные данные: N - натуральное число от 1 до 10^9.
Вывод: наименьшее натуральное число, произведение цифр ктр было бы равно N. -1 - если такого числа нет.
Пример:
N = 11; Answer = -1
N = 12; Answer = 26
N = 14; Answer = 27
Идея: необходимо подобрать такие делители числа, чтобы при их склейке получилось как можно меньшее число.
Например, если N делится на 6, то его делителями также будут 3 и 2. Но в данном случае делитель 6 для нас предпочтительнее, т.к. один разряд 6 < чем два разряда 23 или 32. Соот-но, нам нужно брать как можно большие разряды. Факторизуем наше исходное число N.
- Если есть несколько 2ек, то лучше представить их в виде 4ки, либо 8ки.
- Если есть несколько 3ек, то лучше представить их в виде 9ки.
- Если есть 2 и 3, то лучше представить их в виде 6ки.
- 5 и 7 - простые числа, оставляем их как есть.
- N = 1 - частный случай, обработаем его отдельно. Для N = 1, ответ будет 1.
Если же есть хоть один множитель больше 9, то мы не сможем найти ответ. По сути это все простые числа. Например, для N = 13 нет такого натурального числа, при котором произведение его цифр давало бы число 13, т.к. 13 не раскладывается на множители.
Итак, если обобщить нашу логику, получим, что нам надо нацело делить исходное число на 9, остаток - на 8, его остаток - на 7 и так далее до 2. Если после этих операций мы получим 1, значит мы нашли ответ. Если же в остатке число отличное от 1, значит такого числа нет.
Реализация:
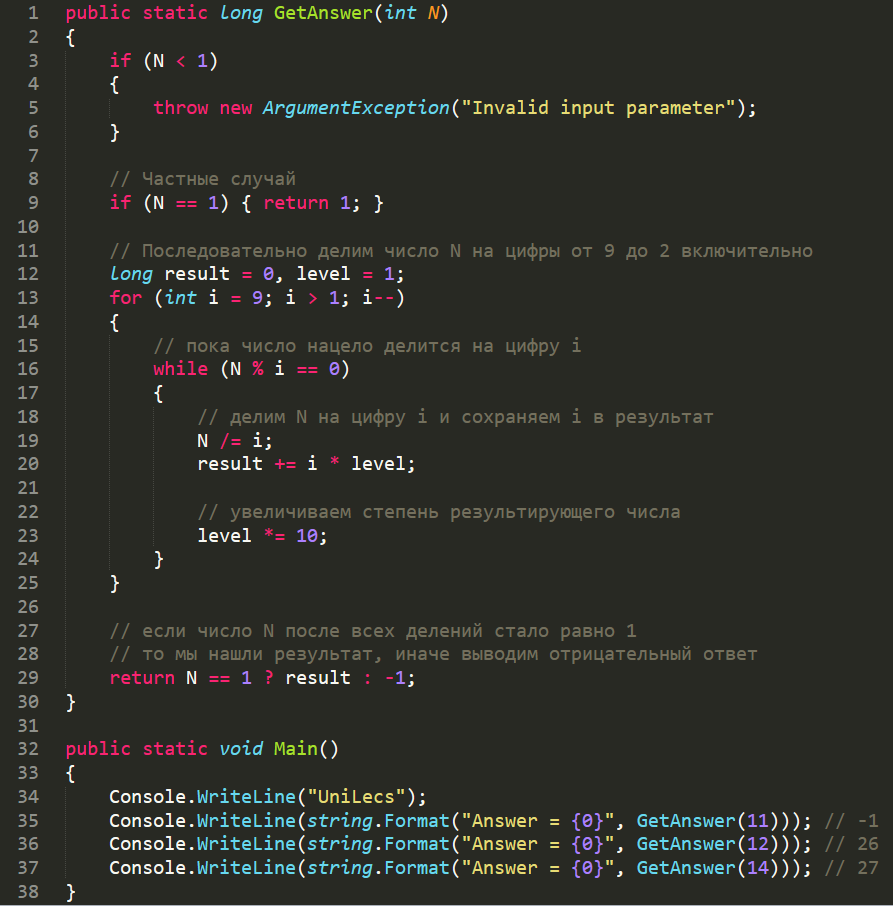
https://gist.github.com/unilecs/3e045d92d679a9de3e57c881b4e221fe
Test: