UniLecs #127. Интервальная сумма
UniLecs
Задача: даны два натуральных числа a, b. Необходимо найти сумму чисел на интервале [a, b] (включая концы интервала).
Входные данные: a, b, где a <= b. a, b от 1 до 10^9.
Вывод: sum - сумма чисел на интервале [a, b].
Пример: a = 1, b = 3
Answer = 6
Идея: в случае, когда значения чисел имеют большой порядок, использовать цикл не только не оптимально, но и невозможно из-за исключений по времени или переполнения типа. Поэтому для нахождения суммы воспользуемся формулами арифметической прогрессии.
S(n) = (a(1) + a(n)) * n / 2, где n - кол-во элементов на интервале
В нашем случае n нам неизвестно, для его нахождения используем формулу n-го члена арифм.прогрессии:
a(n) = a(1) + d (n - 1), где d - разность арифм.прогрессии, ктр в нашем случае равна 1. Тогда получаем, что n = a(n) - a(1) + 1.
Реализация:
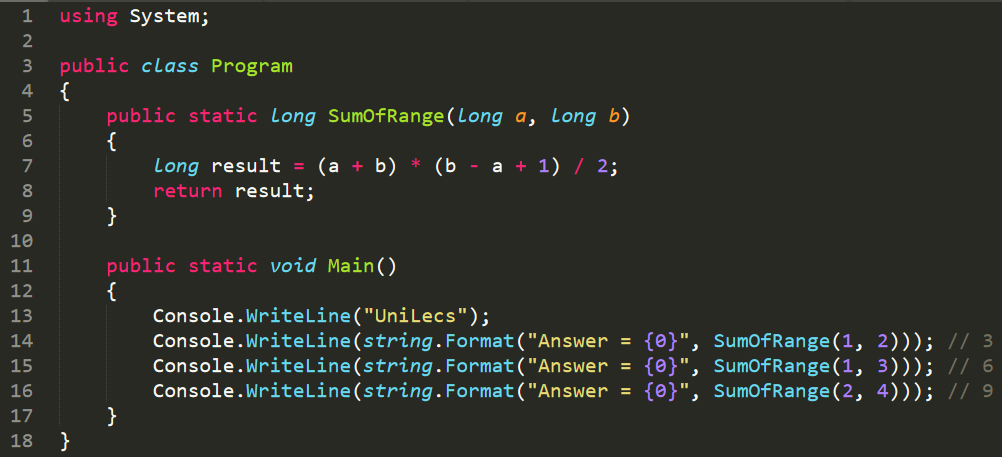
https://gist.github.com/unilecs/38d795778ee78e35f3efb775496c02ab
Test: