UniLecs #118. Сумма на дереве
UniLecsЗадача: дано дерево состоящее из N вершин, каждая вершина имеет значение value. Необходимо определить такое множество вершин дерева, в котором никакие две вершины не имеет общего ребра, и сумма значений в этих вершинах максимальная. Выведите максимально возможную сумму значений в таком множестве вершин.
Входные данные: edges - список ребер, которым задано дерево; каждое ребро определятся двумя вершинами: (i, j).
value - упорядоченный массив значений (от 0 до 1000) в вершинах, где value(i) - значение вершины i (i от 1 до N; 1 <= N <= 10^4).
Вывод: максимальную сумму значений вершин в подмножестве.
Пример:
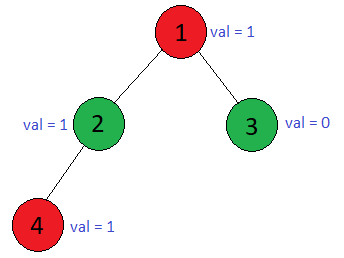
Edges = [ (1, 2), (1, 3), (2, 4) ]
Value = [ 1, 1, 0, 1] (Пояснение: 1я вершина - значение 1; 2я вершина - 1; 3я вершина - 0; 4я вершина - 1)
Answer = 2
Идея: исходя из условий задачи рассмотрим два случая:
Если r - вершина дерева, то будем считать:
- firstSum(r) - макс.сумма значений вершин, ктр можно получить с подмножества вершин с корнем r, если значение в вершине r мы учитываем.
- secondSum(r) - макс.сумма значений вершин, ктр можно получить с подмножества вершин с корнем r, если значение в вершине r мы НЕ учитываем.
В таком случае решение сведется к след.значению:
Max(secondSum(r), secondSum(r)).
Для 1го случая мы учитываем значение в вершине r, поэтому (по условиям задачи) значения с дочерних узлов дерева вершины r мы уже не считаем, тогда получаем след.формулу:
firstSum(r) = value(r) + Сумма(secondSum(t)), где сумма идет по всем дочерних элементам t вершины r.
Для 2го случая, когда мы НЕ учитываем значение в вершине r, и тогда, по условиям задачи, значения в дочерних узлах вершины r мы можем учитывать (можем и не учитывать). В итоге получаем след.формулу:
secondSum(r) = Сумма(Max(firstSum(t), secondSum(t))), где сумма идет по всем дочерним элементам t вершины r.
Детали реализации алгоритма смотрите в комментариях в коде!
Реализация:



https://gist.github.com/unilecs/8ee4878b71c1e9ae2a4fdb5b6b42aef6
Test: