UniLecs #116. Вагонетка
UniLecs
Задача: В одной области одной северной страны, где нет нормальных дорог, чтобы добраться из одного поселка до другого люди вынуждены пользоваться самодельной вагонеткой для доставки грузов. В этой области N поселков и только нектр из них соединены между собой старой железной дорогой. Для проезда по ней из одного поселка до другого нужна одна канистра горючего, но в каждом поселке своя стоимость канистры горючего. А вагонетка слишком мала, и вы не можете взять с собой доп.канистры. Необходимо довести груз из 1го поселка до N-го, при этом использовать минимальное кол-во средств на горючку.
Входные данные: OilCosts = [oilCost_1, oilCost_2, ... oilCost_N] - массив, где oilCost(i) - стоимость канистры горючего в i-м поселке.
TrainRoads = [ (Ai, Bj) ] - массив, где (Ai, Bj) - железная дорога, ктр соединяет поселок Ai c поселком Bj.
Дороги двухсторонние, и разумеется, между любыми двумя поселками не более 1 одной дороги.
Вывод: вывести оптимальный маршрут, т.е. номера поселков на этом маршруте.
Пример:
OilCosts = [5, 10, 1]
TrainRoads = [ (1, 3), (1, 2), (3, 2) ]
Answer: 1 -> 3
Идея: необходимо найти путь с минимальной стоимостью проезда из поселка 1 в поселок N. С таким классом задач отлично справляется Алгоритм Дейкстры - — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Работает только для графов без рёбер отрицательного веса.
Разберем алгоритм Дейкстры более подробно. Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
Рассмотрим след. взвешанный граф:
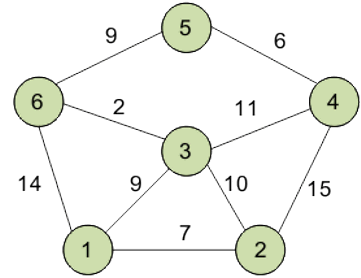
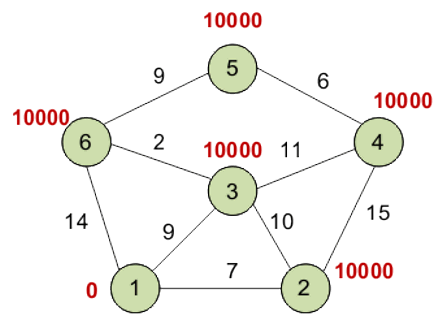
Инициализация данных: метка самой вершины 1 полагается равной 0, метки остальных вершин – недостижимо большое число (в идеале — бесконечность). Это отражает то, что расстояния от вершины 1 до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.
Первый этап: минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Обходим соседей вершины по очереди. Первый сосед вершины 1 – вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1, значению её метки, и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2 (10000), поэтому новая метка 2-й вершины равна 7.
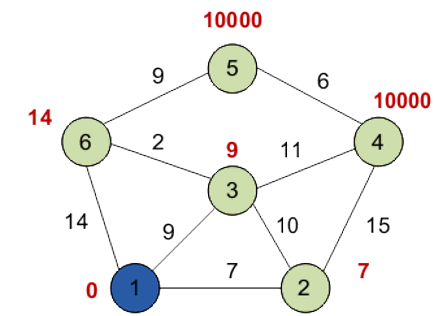
Аналогично находим длины пути для всех других соседей (вершины 3 и 6). Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит. Вершина 1 отмечается как посещенная.
Второй шаг: шаг 1 алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.
Вершина 1 уже посещена. Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а 9 < 17, поэтому метка не меняется.
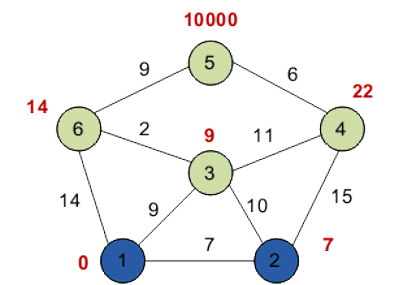
Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет равна 22 (7 + 15 = 22). Поскольку 22<10000, устанавливаем метку вершины 4 равной 22. Все соседи вершины 2 просмотрены, помечаем её как посещенную.
Третий шаг: повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим следующие результаты.
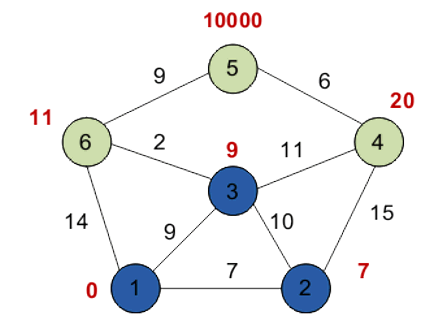
Четвертый шаг:

Пятый шаг:
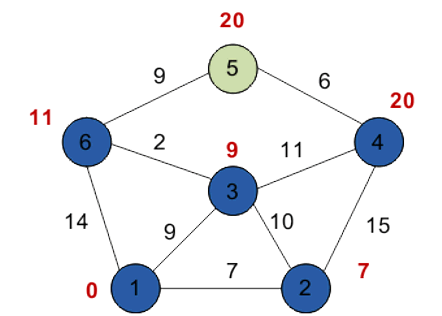
Шестой шаг:
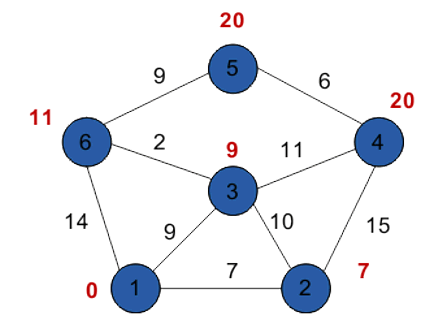
Таким образом, кратчайшим путем из вершины 1 в вершину 5 будет путь через вершины 1 — 3 — 6 — 5, поскольку таким путем мы набираем минимальный вес, равный 20.
Важно отметить, что класс.алгоритм Дейкстры находит кратчайшее расстояние от одной вершины графа до всех остальных. Для того чтобы найти сам кратчайший маршрут, нужно выполнить ряд доп.действий.
Займемся выводом кратчайшего пути. Мы знаем длину пути для каждой вершины, и теперь будем рассматривать вершины с конца. Рассматриваем конечную вершину (в данном случае — вершина 5), и для всех вершин, с которой она связана, находим длину пути, вычитая вес соответствующего ребра из длины пути конечной вершины.
Так, вершина 5 имеет длину пути 20. Она связана с вершинами 6 и 4.
Для вершины 6 получим вес 20 — 9 = 11 (совпал).
Для вершины 4 получим вес 20 — 6 = 14 (не совпал).
Если в результате мы получим значение, которое совпадает с длиной пути рассматриваемой вершины (в данном случае — вершина 6), то именно из нее был осуществлен переход в конечную вершину. Отмечаем эту вершину на искомом пути.
Далее определяем ребро, через которое мы попали в вершину 6. И так пока не дойдем до начала.
Если в результате такого обхода у нас на каком-то шаге совпадут значения для нескольких вершин, то можно взять любую из них — несколько путей будут иметь одинаковую длину.
Более полную информацию по алгоритму Дейкстры и его разбору вы можете найти ниже по ссылкам:
Реализация: в нашей задаче граф будет иметь две дуги с разными весами для двух вершин, т.к. за вес ребра мы будем принимать стоимость канистры в поселке. Для этого нам нужно сделать доп.инициализацию входных данных.
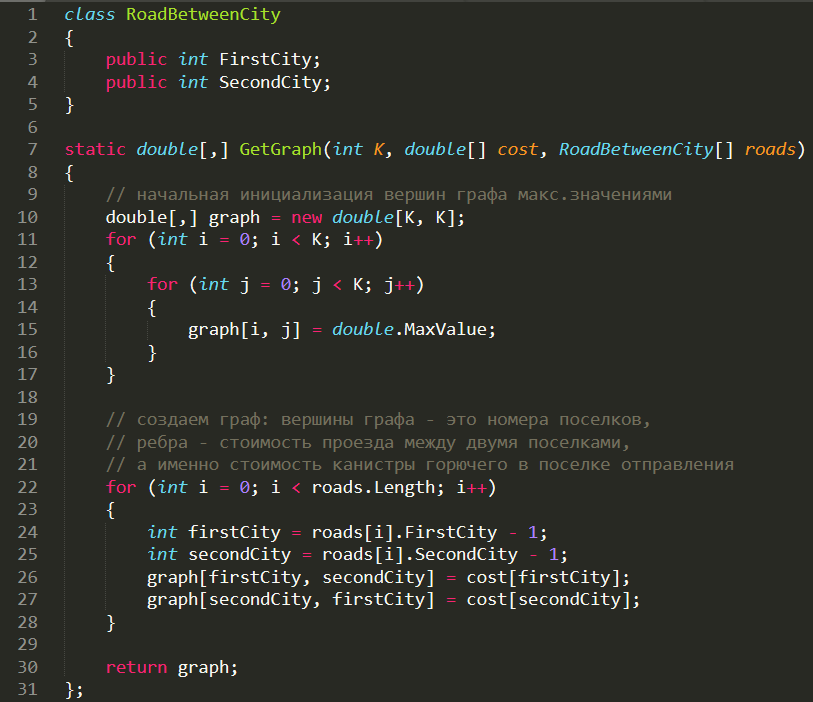
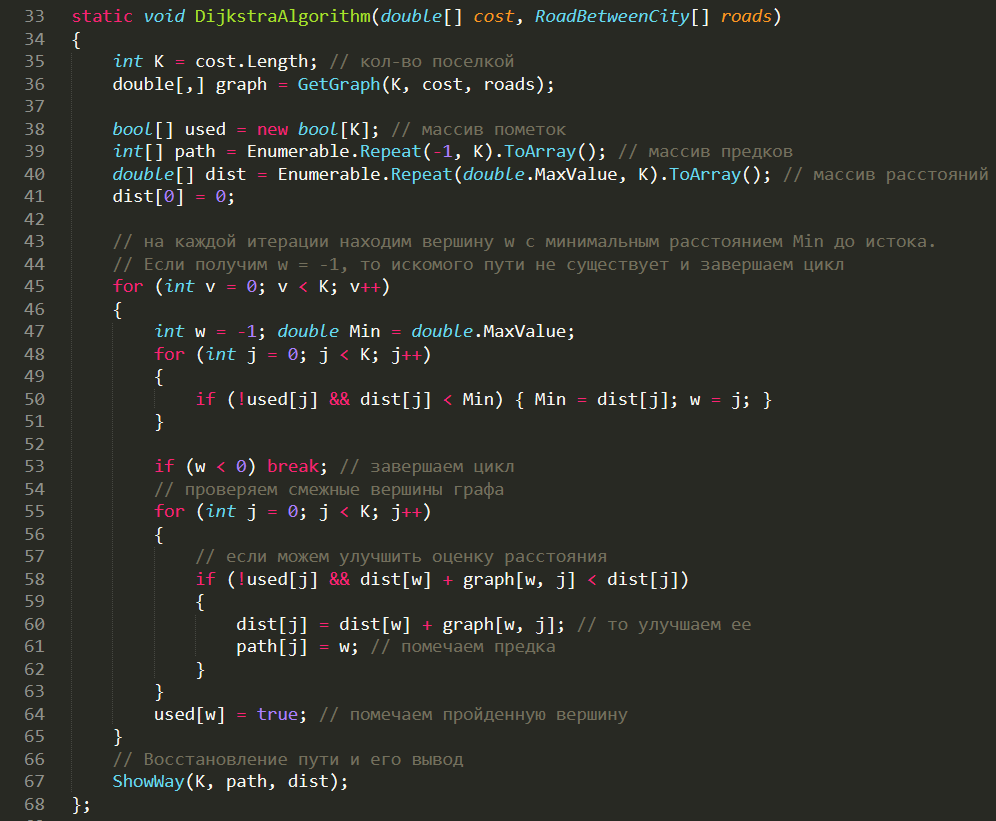


https://gist.github.com/unilecs/7605934bb05bfe90afeddf407bb84990
Test: