Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere

The work from the ICML2020 goes deeper in the understanding of contrastive learning. Authors diverged from a proposal that contrastive loss maximizes the mutual information between the positive views because it was shown that optimizing tighter bound on MI does not provide better results. Instead, the authors built and investigated two intuitive components which are optimized by the contrastive loss.

1. Alignment -- enforces similarity of embeddings of positive samples;

2. Uniformity -- enforces a distribution that preserves maximum information.

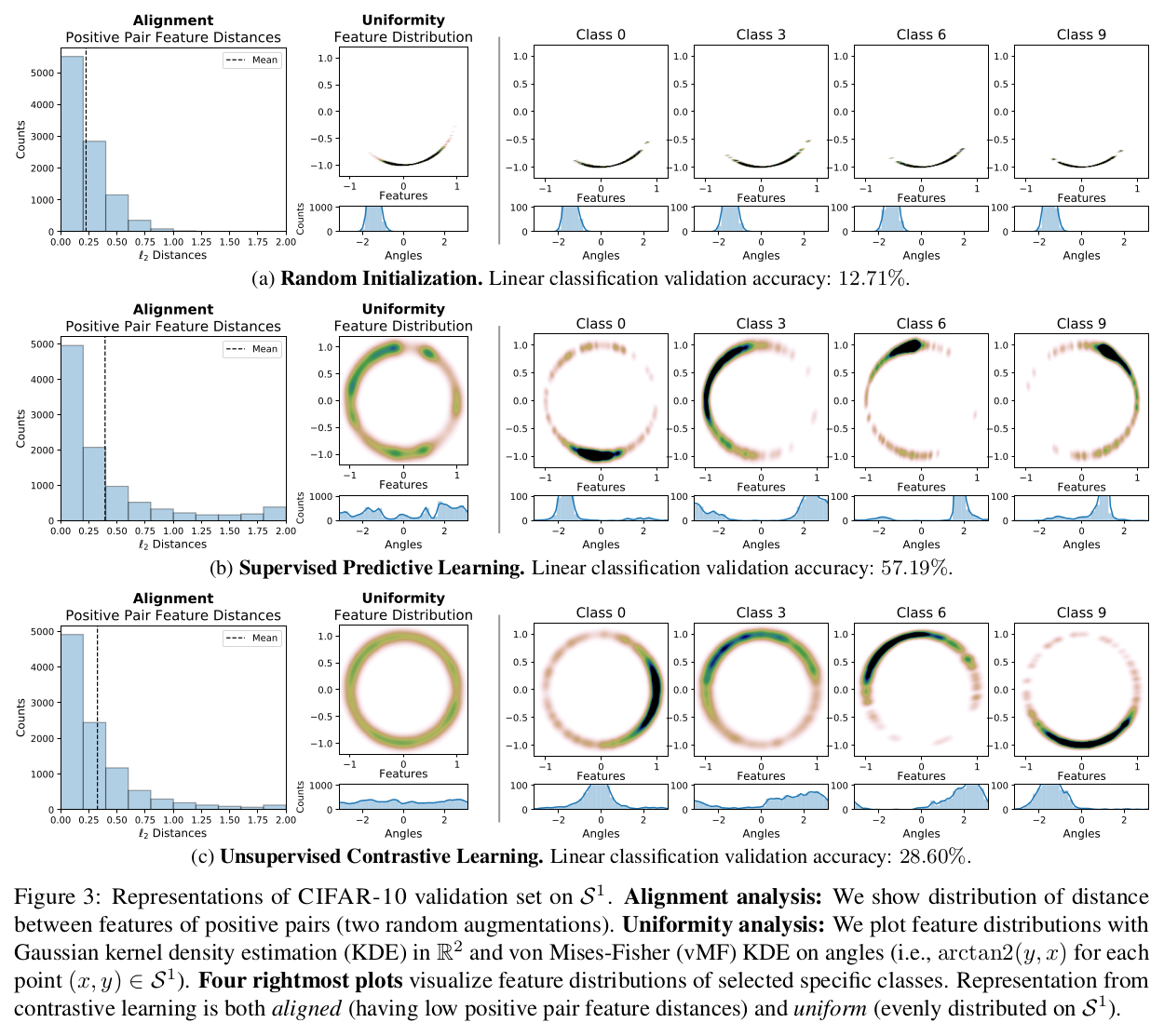
The authors work only with normalized embeddings (i.e., lying on the hypersphere) because this version of embeddings is proven to be superior to non-normalized ones. To show an example, of how practically contrastive loss enforces both, they demonstrated a set of 2D embeddings after random initialization/supervised training/contrastive learning.

The authors then define the alignment loss component simply as the pairwise distance

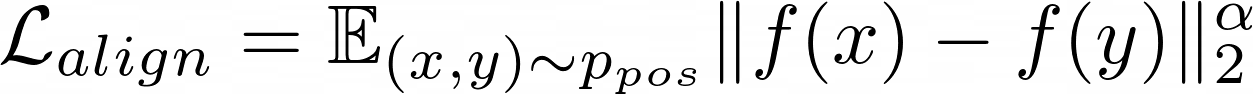
and the uniformity component as a log of Gaussian RBF

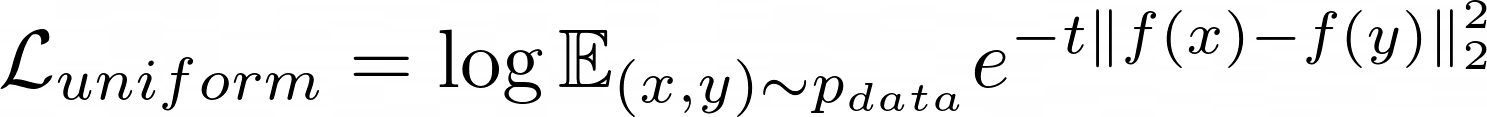
and investigate the properties of losses on text and image classification, and depth estimation downstream tasks.

They found that the proposed losses indeed are both bounded to the good representations, which is shown by downstream task performance increasing with minimization of those two losses, even if the training was performed with the classical contrastive loss.

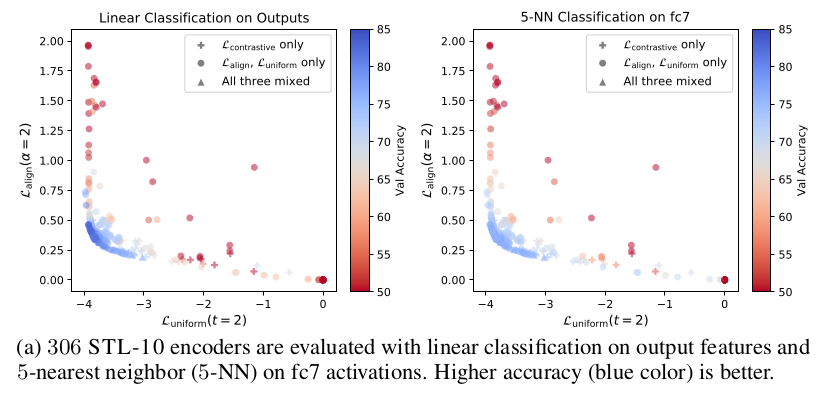
Furthermore, direct optimization of those two losses instead of the contrastive one can further improve the performance.

Authors also assess, that if they use their losses to fine-tune an encoder pre-trained with the classical contrastive loss, the independent application of the alignment or uniformity components will decrease quality. While joint usage increases quality. Which, as the authors claim, proves the causal effect of the losses on the representation quality.