Transformer, explained in detail

Данный блог-пост является конспектом лекции Игоря Котенкова — Transformer, explained in detail. В тексте также есть картинки. Основной массив взят из презентации лекции, доступной здесь.

На этом организационно всё, и поехали!

Первое — что делает трансформер — трансформером?
Ну, товарищи, этим занимаются две его основных составляющие — encoders blocks (энкодер блоки) and decoders blocks (декодер блоки). 

Что такое encoder блоки?

Рассмотрим Encoder блоки. Они ставятся друг над другом — каждый принимает на вход N эмбеддингов размера D и выдает также N эмбеддингов размера D. Внутри каждый энкодер состоит из двух подблоков — механизма self-attention и feed forward neural network.

Рассмотрим каждый.

Feed Forward подблок.

Состоит из двух линейных слоев и нелинейной функции активации между ними. И если вам показалось, что это звучит как двуслойный персептрон — то вам не показалось! =)

Что происходит внутри:

Пусть у вас есть эмбеддинг размера D_m. Подадим его в FF подблок. Внутри произойдет следующее: эмбединг D_m будет разжат в эбмденнинг размера D_ff и после снова возвращен к размеру D_m (ff > m). О размерах разжатий видео 40:50.

И всё. Вот такие они простые. Но просты, да интересны:

FF слои содержат от 65 до 75% параметров модели и, таким образом, грубо говоря в них основные «знания» модели. 

Чем выше уровень энкодера, тем более семантические сложные паттерны находят FF блоки (и чем ниже, тем более простые).

Важно: может показаться, что раз уж больше FF слоев дают более семантически сложные выходы, то хорошо бы настакать кучку — именно такой вопрос был задан в видео 45:10. Но больше не всегда равно лучше — во-первых, затухают градиенты, во вторых, увеличивается вычислительное время (дольше работает модель). Да и иногда можно получить same качество, если из количества блоков параметры перетащить в количество параметров на блок.

С Feed forward'ами всё.

Теперь вишенка — то, что в оригинальной статье выглядит так:

Self-attention подблок.

Интуитивная суть подблока — для каждого слова считаем связи с остальными словами. Стоит он на трех матрицах — Q-queries, K-keys, V-values.

И так пусть у нас есть задача рассчитать взаимосвязи слов в некоторой последовательности и пусть последовательность состоит из двух слов: Thinking machines.

1. Для каждого из слов получим его представление в виде эмбеддингов и проведем матричное умножение вектора на каждую из матриц, получив таким образом для каждого векторА запроса, ключа и значения.

machines (q1, k1, v1)

thinking (q2, k2, v2)

2. Рассмотрим слово thinking и поставим задачу исследовать, как оно связано с остальными (в примере только с одним — словом machines и с самим собой). Вооружимся вектором запроса — он будет играть роль «флага связи».

Тогда:

relationship1 = q1*k1 (связь слова с самим собой)

relationship2 = q1*k2 (связь слова со словом два)

Вдумчивые читали обратили внимание, что производится умножение векторов. С математической точки зрения берется скалярное произведение (dot product) и его результатом не вектор, а скаляр (число). Чем выше значение дот продукта, тем более близки векторы — чтобы узнать почему это так и что такое dot product видео 53:43.

Далее, во избежание больших числовых значений и взрыва градиентов, полученные дот-продукты нормируются на корень из размерности одного из эмбеддингов (напомню, ранее было замечено, что для подачи в слой FeedForward все эмбединнги должны быть одного размера. Однако слово «одного из» не случайно, так как существуют статьи, экспериментирующие с размерами эмбеддингов видео 1:03:00). Зачем это так и почему это происходит математически, видео 58:00.

После значения пропускаются через софтмакс (таким образом на выходе получается, что сумма всех значений (а у нас это связи слов друг с другом) равна 1). И таким образом, после всех манипуляций мы получаем score1 (связь слова с самим собой) и score2 (связь слова со словом 2).

Матрица всех скоров (а у нас их два) будет квадратной. И именно она является матрицей внимания (Attention matrix). Важно, что алгоритмическая сложность вычисления этих софтмаксов O(n^2) — квадратично зависит от количества входных токенов, поэтому важно помнить о качественном обучении токенизатора — иначе модель будет работать более медленно. Есть также статьи с модификациями attentions (видео 1:06:22).

Важно: при обучении декодера используется так называемое Masked-self attention — значения скоров, расположенные выше главной диагонали матрицы Attention преобразовываются в минус бесконечность, и только после они подаются софтмаксу. Зачем это — чтобы при обучении декора не было «взгляда в будущее». Подробнее об этом 1:43:40

Теперь моргаем глазами, если вы немного устали, и достаем вектора v1, v2!  И умножаем их на соотвествующие им scores:

out1 = score1*v1
out2 = score2*v2

Полученные out’ы суммируем и получаем z1 = out1 + out2.

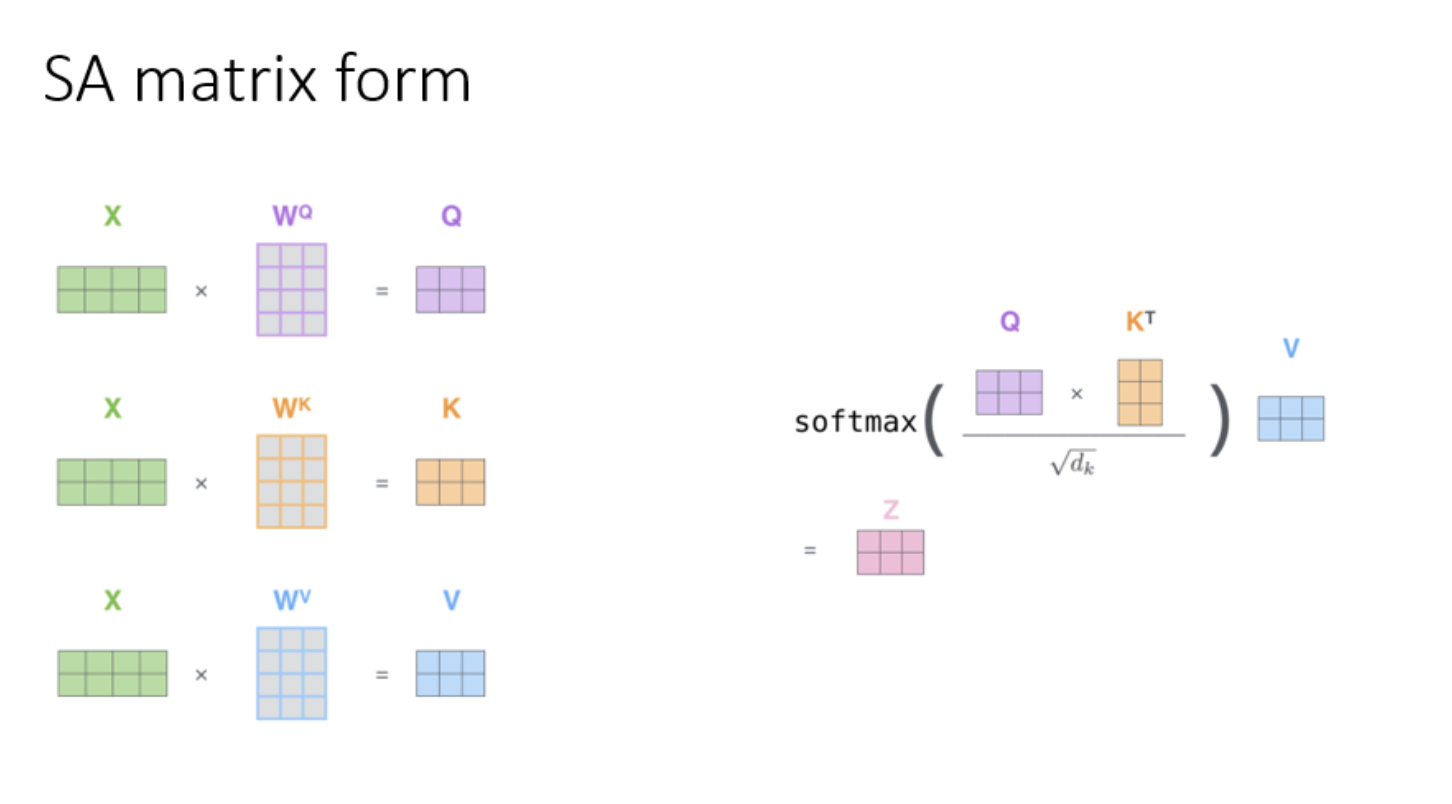
И полученный (словарем меня за тавтологию) z1 у нас — взвешенная сумма. Картинка  и объяснение того, как это выглядит в матричном виде видео 1:16:16 — аккуратно по одному, как вышивку  крестиком необходимости вычислять нет. Мы просто берем матрицу эмбеддингов, и умножаем на каждую их матриц Q, K, V получая соотвественно матрицы Qe, Ke, Ve — всех запросов, ключей и значений. После матрицу Qe*Ke.T, где.T означает транспонирование (операция, чтобы размерности матриц согласовывались), полученный выход нормируем на константу и умножаем на матрицу V - values, получая матрицу Z.

 Механизм Multi-Head Attention или откуда у моделей берутся головы.

Если вы слышали про «головы трансформеров» – то теперь вы знаете, что это. Действительно знаете — это просто несколько троек матриц Q, V, K, «смотрящие» на разные части связей (они сами выучивают эти связи или они как-то изначально задаются? Похоже, сами). В таком случае у нас получается несколько (сколько и голов) матриц Z, которые стакаются друг над другом и умножаются на матрицу, которую мы раньше не видели — W и получаем итоговую матрицу эмбеддингов Z (пусть это будет Z-красивая, как говорил мои преподаватели по алгебре, когда буквы заканчивались =)).

Как учесть порядок слов? Позиционное кодирование. 

Для такого, чтобы модель понимала порядок слов в модели есть еще одна матрица — матрица позиций слова. Где она находится и что собой представляет?

Пусть у нас есть последовательность слов  те же Thinking machines, с токенами thinking и machines и эмбеддингами x1, x2. Положив эмбеддинги друг под друга (стакнув их) получим матрицу эмбеддингов X. Далее случайным образом инициализируем матрицу Pos — для отражения позиций. Она будет иметь размер в длину размер последовательности (у нас — 2) и в ширину длина эмбеддингов (пусть у нас это будет 3). 

И всё, перед входом в Encoder мы просто складываем две матрицы, получая вектор с «позиционным секретом».

Для дальних слов существуют модификации и трюки, например вычисление только первых нескольких позиций, подробнее видео 1:20:50 или ещё описано здесь.

Как эта машина, учитывая кучу слоев, не затухает? Residual connection and Layer norm.

Что такое layer norm — дословно нормализация слоя. Мы берем матрицу исходных эмбеддингов X и складываем с Z-красивое (X+Z). Для этой суммы находим среднее  (mean) и стандартное отклонение (std). И нормируем сумму, приводя её к распределению со средним 0 и стандартным отклонением (и дисперсией откуда) 1.  Если прописать код, то:

a*((X+Z) - mean)/(std + epsilon) + b

Что за a и b? Также некоторые обучаемые параметры, зачем нужны и что за в видео 1:30:50.

Что такое residual connection? Тут также — буквальный перевод «соединение остатков» отлично его описывает. Пусть у нас есть вектор признаков x, к которому мы хотим применить произвольный слой трансформера — sublayer. Где тут роль residual connection. При прямом проходе по сети (forward pass) мы применяем sublayer к вектору x, получив какой-то x’ (x преобразованный) и к этому преобразенышу добавляем оригинальный вектор. Полученная сумма будет участвовать уже в расчете градиентов этот трюк поможет избежать их затухания. 

Decoder блок.

Состоит из тех же компонент, что и энкодеры, но с одной новинкой — encoder-decoder attention(a.k.a cross attention). Он лежит ровно после self-attention и до FF блока. Что собой представляет:

После прохода через self attention у нас, напомню, есть запросы, ключи и значения (q1, q2, k1, k2, v1, v2).

В decoderе в это время инициализируется некоторый первый вектор (например, это может быть вектор, отвечающий служебному токену о начале предложения) и его эмбеддинг. Чтобы далеко не отходить от служебных токенов, назовем этот вектор servant.

Как мы делаем Attention.

Напомню, что Attention — это матрица скоров, позволяющая взять векторы, играющие роль в предсказании с определенным весом. И что изначально мы решаем задачу перевода (хотя сейчас трансформеры лежат в основе мультимодальных моделей).

Проясню также, что после прохода через стек энкодеров у нас есть 1 эмбеддинг. На вход декодеру подаются эмбеддинги декодера (инициализированный вектор в нашем случае), и эмбеддинги энкодера тоже.

Внутри cross-atention “уже сидят матрицы QKV” (цитата Игоря — пришлось "пристать" к нему, чтобы понять этот блок:)) — как в привычном attention блоке. Для того, чтобы сделать cross-attention мы

- берем то, что получили из энкодера и вычисляем для этого Keys и Values

- берем то, что есть в декодере (у нас это вектор servant) и вычисляем для него Q. И также получаем (q’1, k’1, k’2, v’1, v’2). Штрихи — чтобы подчеркнуть, что это не то же самое, что было вычисленно ранее. 

Чтобы совсем сделать attention в декодере мы берем запрос вектора servant и скалярно умножаем его на k’1 и k’2, получая 2 значения. 

Поскольку servant является запросом, мы как бы меряем связь между ним и каждым словом в декодере, что интуитивно похоже на ответ вопросу «Это ты должен быть, как перевод или нет»?.

Полученные два значения мы также нормируем и пропускаем через софтмакс — и таким образом получаем нашу матрицу attention’s. В отличие от эенкодера она не квадратна — сейчас размера 1x2 (1 строка, 2 столбца). 

Дальше мы берем вектора v1 и v2, умножаем их на полученные веса, суммируем, получаем итоговый вектор и отправляем в FF слой и дальше — чтобы выпечь предсказание. 

Данный процесс будем повторять итеративно, в нашем случае два раза, пока не дойдем до завершения задачи. Визуализация этого процесса для трех слов на видео 1:40:25. 

Как производится предсказание. 

Если посмотреть на архитектуру трансформера, то после последнего декодера написано следующее: linear+softmax. Если вы знакомы с принципом работы функции софтмакс и с линейными слоями, то здесь отличий нет.

После всех декодеров у нас есть некоторый вектор. Мы этот вектор, подаем на входной слой полносвязный нейронной, выходным слоем которой является вектор, с размерностью, равной размерности словаря (количества уникальных токенов, в нашем примере их 2). Значения данного вектора мы пропускаем через софтмакс (чтобы получить вероятности) и дальше из словаря достаем слово, чей индекс соответствует индексу с максимальной вероятностью.

Визуально и вслух этот процесс объяснен в видео 1:42:00. 

Ну вот и всё! С архитектурой разобрано!)
Буду рада видеть вас в дата-блоге: https://t.me/jdata_blog
И также оставляю ссылку на блог Игоря: https://t.me/seeallochnaya

А на вкусненькое — еще пара абзацев.

Трансформеры BERT и GPT – структурное отличие.

BERT состоит только энкодеров, а GPT только из декодеров (там уже нет cross-attention’a, только masked self-attention). Задача GPT — предсказание следующего слова, задачи BERT’a же формируются иначе.

BERT и его задачи это:

1. Masked Language Modeling (MLM) — восстановление замаскированной части данных, совсем подробно про MLM (1:54:58). Задача в настоящее время масштабирована и изучена в случае, когда выкинутой маской является параграф или отдельные предложения.
2. Next Sentence Prediction (NSP) — определение, относятся ли два входных предложения к одному контексту, совсем подробно про NSP, а также о возможном расширении применения служебных токенов видео 1:58:40.

Самое последнее служебные токены в BERT:

Для MLM:

[MASK] — токен замаскированной части

<eos> — конец последовательности;

Для NSP:

[CLS] —  токен, отвечающий за контекст предложения, вбирает в себя информацию о контексте двух предложений в обучающем наборе данных, по сути «красный флаг» для выхода — да, эти ребята из одного контекста или нет;

[SEP] — «аналог точки», конец предложения (контекста), с данным токеном связано существование еще одной матрицы в BERTe (наряду с позиционной) — segment embeddins, подробнее, представление текста в BERTe (2:02:50)

На этом прощаюсь!

Чудесного вам времени суток — утра, дня, вечера или ночи,
Ваш Дата-автор)