Топ 3 статистических парадокса в Анализе Данных

Вопросы по статистике ждут любого кандидата, подающегося на позиции Data Science, аналитику и нередко менеджмент. Сегодня обсудим самые популярные и важные парадоксы на классических примерах. Очень будет полезным, если после знакомство с каждым парадоксом, вы зададите вопросы в духе: почему этот парадокс вообще важен? какое у него значение в процедуре AB тестирования или алгоритмах ML? из-за чего случился этот парадокс, как его избежать? Делитесь своими впечатлениями в комментариях!

1. Парадокс Симпсона

Рассмотрим пример, описанный известным популяризатором математики Мартином Гарднером. Пусть мы имеем четыре набора камней. Вероятность вытащить чёрный камень из набора №1 выше, чем из набора №2. В свою очередь, вероятность вытащить чёрный камень из набора №3 больше, чем из набора №4. Это значит, что в наборе №1 чаще встречаются чёрные камни, чем в наборе №2, а в наборе №3 чаще, чем в наборе №4. Объединим набор №1 с набором №3 (получим набор I), а набор №2 — с набором №4 (набор II). Совершенно очевидно, что вероятность вытащить чёрный камень из набора I больше, чем из набора II, ведь в набор I попали те наборы, где чёрные камни были «гуще»! Однако, в общем случае такое утверждение неверно, и мы сейчас приведём пример расположения чёрных и белых камней в наборах, когда это совершенно «очевидное» условие не выполнится. Пусть в наборе №1 6 чёрных и 7 белых камней, в наборе №4 4 чёрных и 5 белых камней, в наборе №3 6 чёрных камней и 3 белых, в наборе №4 9 чёрных камней и 5 белых. Тогда в наборе №1 чёрные камни «гуще», вероятность вытащить чёрный камень из первого набора выше. Действительно, в наборе №1 всего 13 камней, из них 6 чёрных, значит, вероятность вынуть чёрный камень составляет 6/13. В наборе №2 всего 9 камней, из них 4 чёрных, значит, вероятность вынуть чёрный камень составляет 4/9. Мы видим, что 6/13 > 4/9, значит, вероятность вынуть чёрный камень из набора №1 выше. Сравним теперь наборы №3 и №4. В наборе №3 6 чёрных камней, а всего камней 9, значит вероятность выбрать чёрный камень составляет 6/9. Для набора №4 эта вероятность равна 9/14. Мы видим, что 6/9 > 9/14. Итак, наборы № 1, 2, 3 и 4 удовлетворяют тем требованиям, которые мы предъявили в постановке задачи. Теперь смешаем наборы №1 и №3 (т. е. те, где чёрные камни лежат «гуще») и наборы №2 и №4, т. е. «менее чёрные» наборы. Каково же соотношение чёрных и белых шаров в наборе II - смеси «более чёрных» наборов №1 и №3? Там будет 12 чёрных и 10 белых камней, т. е. вероятность вынуть чёрный камень равна 14/22. Во наборе II, собранном из «менее чёрных» наборов №2 и №4 будет 13 чёрных и 10 белых шаров, т. е. вероятность вынуть чёрный шар составит 13/23. Итак, набор II, собранный из «менее чёрных» наборов №2 и №4 загадочным образом оказался более чёрным! Если разобранный выше пример выглядит несколько загадочно, то второй пример сделает парадокс Симпсона простым и понятным. Рассмотрим опять 4 набора чёрных и белых шаров. Только теперь соотношение чёрных и белых шаров наборах будет таким (см. табл. 1).

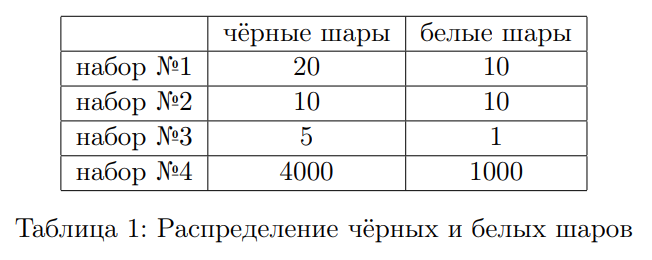
Мы видим, что снова выполнены все требования условия задачи: набор №1 «более чёрный», чем набор №2, набор №3 «более чёрный», чем набор №4. Однако, набор №4 все же более чёрный и чем набор №2, и чем набор №1, и он куда больше, чем оба эти набора. Т. е. именно состав набора №4 будет решающим в смеси наборов №2 и №4. Итак, мы видим, что набор I теперь состоит из 25 чёрных и 11 белых шаров, вероятность вынуть чёрный шар оттуда составляет 25/36 = 0, 69444. Набор II состоит из 4010 чёрных и 1010 белых шаров, и он гораздо «более чёрный» — вероятность вынуть из этого набора чёрный шар составляет 4010/5020 = 0, 7988. 

2. Феномен Уилла Роджерс

Феномен Уилла Роджерса близок к парадоксу Симпсона, фактически, в нем описывается тот же эффект, только в других терминах. Название этого парадокса основывается на следующей цитате, приписываемой комедианту Уиллу Роджерсу: «Когда оки покинули Оклахому и переехали в Калифорнию, они повысили средний интеллект обоих штатов» (оки — презрительное или просторечное название жителей Оклахомы). Итак, вопрос. Пусть есть два множества чисел А и В, например, наборы IQ двух классов. Может ли такое быть, что при перемещении каких-то чисел из множества А в множество В среднее значение обоих этих множеств повысится? Задумаемся: для того, чтобы после перемещения кого-то из А в В среднее значение А повысилось, множеству А нужно «избавиться» от какого-нибудь маленького числа, классу А избавиться от плохих учеников. Может ли при этом повыситься средний уровень класса В? Очевидный ответ — нет, не может — снова неверен. Действительно, рассмотрим такие множества: 𝐴 = {10, 20, 30, 40, 50} и 𝐵 = {1, 2, 3, 4, 5} 

Среднее значение множества А составляет

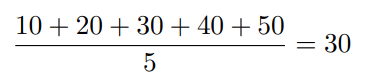
Ясно, что если мы выкинем из множества А самое маленькое число 10, то среднее станет больше. Действительно, без 10 оно составит

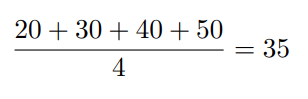
Однако, для множества В число 10 не маленькое, а наоборот — большое. Если без него среднее в множестве В составляло (1 + 2 + 3 + 4 + 5) /5 = 3, то теперь среднее будет больше: 

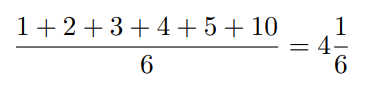
Итак, повышение среднего в обоих множествах возможно, и шутка Уилла Роджерса (за которую мы никак не отвечаем) означает, что жители штата Калифорния глупее самых глупых оки.

3. Парадокс Берксона

Парадокс Берксона или ошибка Берксона состоит в неверном заключении о зависимости событий А и В, если мы наблюдаем только те исходы, для которых выполняется хотя бы одно из событий А или В. Пусть в городе А живёт 100 девушек, из них 10 красавиц и 10 умниц, причём события «случайно выбранная девушка — умница» и «случайно выбранная девушка — красави ца» независимы, т. е. ровно одна девушка и умница, и красавица. Действительно, если среди всех девушек 1/10 часть составляют умницы, то для того, чтобы эти события были независимы, среди красавиц тоже должна быть 1/10 умниц, т. е. умниц—красавиц будет (1/10) × 10 = 1. Посмотрим теперь на эту же ситуацию с точки зрения жителя соседнего города, которо му рассказывают только об интересующих его девушках: умницах или красавицах. Он знает о 19 девушках из этого города: 10 умниц, 10 красавиц, но единственная умница—красавица посчитана и в том и в другом десятке. Итак, с точки зрения этого наблюдателя, вероят ность того, что девушка умница составляет 10/19, вероятность же, что девушка умница, при условии, что она красавица, составляет все ту же 1/10. Итак, на взгляд этого наблю дателя, события зависимы, у них есть обратная связь — среди красавиц реже встречаются умницы, думает он, чем среди всех девушек. Тот же эффект наблюдают врачи, биологи, многие специалисты, которые вполне всерьёз занимаются данными. Врач сравнивает частоту тех или иных заболеваний среди тех, кто к нему обращается, т. е. среди тех, кто чем-то болен. Подумайте сами — в каких ситуациях вы сталкивались с тем, что делаются слишком поспешные выводы о подобной зависимости.