Тетради Рамануджана в жаркое лето

Автор: Джумадильдаев Медет

Редактор: Машуров Нариман

Однажды я наткнулся в интернете на 2 тома книг Брюса Берндта о тетрадях Рамануджана. Одна из задач - решить уравнение x!+1=y^2 в натуральных числах - очень заинтересовала меня. Первые три решения очевидны: (x,y)=(4,5),(5,11) и (7,11), однако необходимо найти еще и четвертое.

На первый взгляд, задача тривиальная, поэтому хочется попробовать решить ее при помощи компьютера. Но уже скоро компьютер начинает сходить с ума, пытаясь подставить значения х больше 30. Таким образом, все современные достижения человеческой науки оказываются бессильными перед простой задачей с двумя неизвестными.

Вскоре начинаешь понимать, что никакой искусственный интеллект со всеми компьютерами на свете не в силах решить это уравнение. Для этого нужно хотя бы понимать, что такое целое число и как отличить его от нецелого. А чтобы «узнать» это, необходимо углубленно изучить теорию чисел. Поэтому я решил отложить эту задачу на будущее, пока не получу нужные знания.

Я обратил внимание на биографию автора и на другие его задачи. Сриниваса Рамануджан Айенгор (22 декабря 1887 – 26 апреля 1920) - гениальный математик современности. Имея с детства большую склонность к математике, он зарабатывал на жизнь, работая бухгалтером в порту Мадраса. К счастью, начальник, заметив его увлеченность вычислениями, не стал препятствовать его научным изысканиям. И в его тетрадях вперемежку с бухгалтерскими отчетами появлялись различные формулы и теоремы. Некоторые из них вызывают изумление, ведь до сих пор неизвестно, как он сумел к ним прийти.

Рамануджан опубликовал немного научных статей, однако оставил после себя целых 30 тетрадей, и некоторые из них удалось разобрать и опубликовать. Их содержимое вызывает удивление и восторг у людей, близких к математике. Одним из них является известный профессор Кембриджского Университета Годфри Харди. По его словам, “каждое натуральное число было личным другом Рамануджана”.

При жизни не все работы Рамануджана были признаны достойным образом, но сейчас он обрел славу гения и право стоять в одном ряду с величайшими учёными всех времён. В его честь издаются журналы и проводятся конференции. Правительство Индии учредило стипендии, которые носят его имя. Академии и студенты борются за звание быть лауреатами его премии. Про него был создан фильм “The Man Who Knew Infinity”. Его имя носят два научных журнала.

Одним из его достижений являются сравнения чисел секанса. Напомню, что секанс – это тригонометрическая функция, обратная косинусу. Коэффициенты ряда Тэйлора секанса имеют хорошую комбинаторную интерпретацию. Чтобы определить секансовы числа введем несколько определений. Перестановка называется альтернативной, чередующейся или зигзаг-перестановкой, если ее подъемы и спуски чередуются.  Число зигзаг-перестановок n чисел называется числом секанса En^1, если n - четное. При нечетном n, число зигзаг-перестановок называется числом тангенса.

Например, 2413 – зигзаг перестановка, поскольку 2 < 4 > 1 < 3 . Вот перестановки для четырех чисел: {1324, 1423, 2314, 2413, 3412}.  Поэтому четвертое число секанса E4 = 5 .

Вот первые шестнадцать чисел секанса со знаками:

0,-1,0,5,0,-61,0,1385,0,-50521,0,2702765,0,-199360981,0,19391512145.

Заметим, что каждое четвертое число секанса в этом ряду, а именно, 5, 1385, 2702765,  19391512145, при делении на 60 даёт остаток 5, и каждое четвертое число секанса начиная со второго -1, -61, -50521 , -199360981 при делении на 60 даёт остаток -1. Это и есть замечательная теорема Рамануджана о сравнениях чисел секанса:

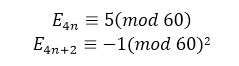
где Ei есть i-тое число  секанса.

Мне захотелось распространить сравнения Рамануджана для чисел секанса на числа тангенса. Несложно установить, что

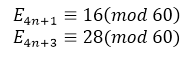
Компьютерные вычисления показали, что базу сравнения (число 60) можно улучшить. Сравнительно легко доказать, что, например,

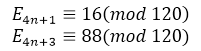
Возникает естественный вопрос о том, действительно ли число 120 самое оптимальное. Можно ли и его увеличить, чтобы сравнения сохранялись для любого ? Ответ меня удивил. Сравнения будут оставаться верными, если заменить 120 на 180, 360 и так далее. Теперь возникают новые вопросы. До какой степени допустимы такие увеличения? Остановится ли процесс оптимизации? Если да, то когда?

Карантин позволил мне дать полные ответы на эти вопросы. Оказывается, что база сравнения для тангенсовых чисел - 720, что 12 раз больше, чем база сравнения для чисел секанса!

Основной результат о сравнениях чисел тангенса формулируется так:

Теорема 1.

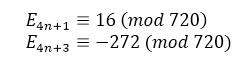
База сравнения дальше не улучшаема: замена числа 720 на большее число нарушит сравнения.

Имеется множество различных способов представления чисел Эйлера[3] для доказательства этой теоремы. Вот один из них. Число Энтрингера E(n,k) – число перестановок чисел 1, 2, ...n+1 , которые начинаются с числа k+1, и чередуются после падения (второе число меньше первого, а дальше знаки чередуются). Рекуррентная формула определяется следующим образом.

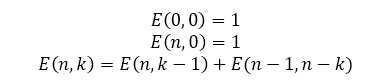
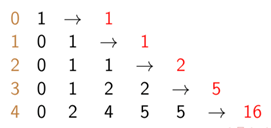
Как получить числа секанса и тангенса с помощью этой формулы? На картинке ниже красными отмечены суммы рядов, соответствующие числам Эртрингера. Они и дают искомую последовательность чисел, так как  (так как справа и слева в этой формуле – количество зигзаг-перестановок, посчитанное сначала через числа Эртрингера, а затем через число Эйлера).

Введём ещё одно Определение. Полином Эйлера задается так:

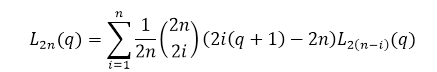
Например,

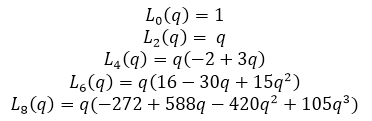
Мой основной результат таков:

Теорема 2.

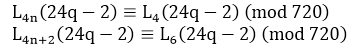
Теорема 1 следует из теоремы 2 при q = 0 .

Основным инструментом доказательства служит Китайская теорема об остатках. Из-за того, что 720=5 * 3^2 * 2^4, а 5, 9 и 16 - взаимно простые числа, по Китайской теореме об остатках теорема 2 распадается на три различных случая. Каждый из этих случаев доказывается с помощью метода математической индукции.

При работе над данным проектом я часто использовал компьютерные вычисления для определения закономерностей в значениях полиномов, значений параметров, и выбора формул. Программный код занимает более тысячи строк.

Изначально я пробовал использовать вышеперечисленные интерпретации числа Эйлера, чтобы найти закономерности и использовать их в дальнейшем для доказательства теоремы. Оказалось, что достаточно было использовать полином Эйлера, который обладает рядом нужных свойств.   

Тем не менее, было трудно определить нужный параметр, при котором можно было добиться оценки 720. Для этого я заметил следующие сравнения.

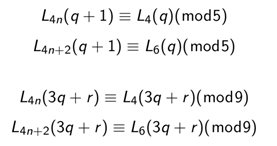
Здесь становится понятно, что параметр следует заменить на 24q - 2. После этого проблем с основным доказательством нет. Индукционные переходы легко выполнимы, что позволяет успешно завершить удивительное путешествие в мир Рамануджана.

[1] С точностью до знака (здесь и далее – прим. ред.).

[2] Здесь и далее запись  a = b (mod m) означает, что числа a и b дают одинаковый остаток при делении на m.

[3] En, чисел секанса и тангенса.