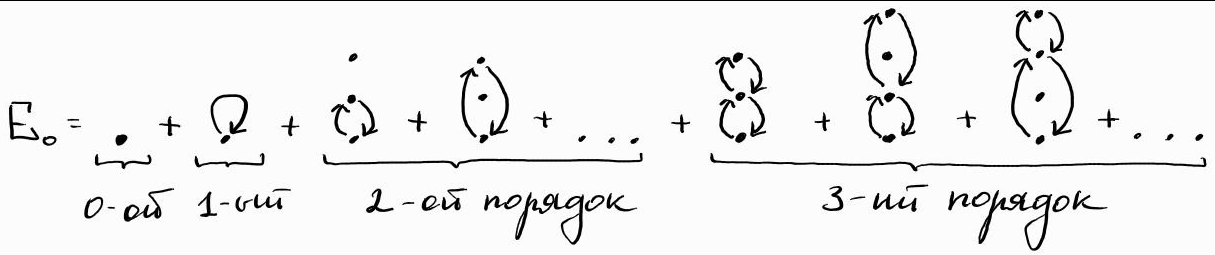Теория возмущений

Обозначения

Квантовые системы могут находиться в особых состояниях, которые называются собственными. Они схожи с равновесными состояниями из классической физики. В частности, собственные состояния не меняются во времени, то есть если система оказалась в одном из них, то останется в нём навсегда. Определение собственных состояний и соответствующих им энергий даёт полную информацию о квантовой системе, возможность вычислить любую величину и предсказать её эволюцию.

Для описания квантовых систем нам будет удобно пользоваться обозначениями Дирака. Собственное состояние квантовой системы будем обозначать как

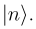
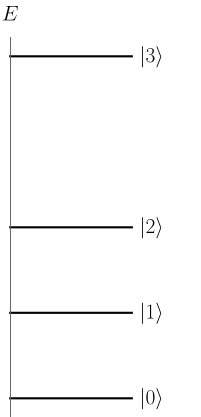
Здесь внутри скобок может быть, вообще говоря, любой символ, который нам кажется подходящим. В нашем случае n это просто целое число — номер собственного состояния. Отсортируем состояния по возрастанию их энергии и начнём нумерацию с нуля. То есть, |0> это состояние с наинизшей энергией, |1> — следующее за ним и т.д., см. рисунок ниже.

На квантовые состояния могут действовать операторы, математически описывающие физическое взаимодействие. Для дальнейшего изложения детали неважны, надо только знать, что оператор это нечто, изменяющее квантовое состояние. Запись

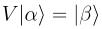
означает, что под действием оператора V система из состояния |α> перешла в состояние |β>. Греческие буквы выбраны, чтобы подчеркнуть общий характер выражения, не привязанный к набору состояний |n>.

Далее ключевое значение будет иметь выражение

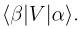
Это так называемая амплитуда плотности вероятности того, что благодаря взаимодействию V произойдёт переход из состояния |α> в состояние |β> (а может ведь и в какое-то другое). Амплитуда вероятности является просто числом, вообще говоря, комплексным, а квадрат её модуля есть вероятность процесса "состояние |α> переходит в состояние |β> благодаря взаимодействию V". Например, если амплитуда вероятности равна 1/2, то вероятность процесса равна 1/4.

Ряд теории возмущений

Теория возмущений решает следующую задачу: пусть при отсутствии взаимодействия (V = 0) нам известны собственные энергии системы и соответствующие им состояния. Как изменятся собственные энергии и состояния системы, если включить слабое взаимодействие V (его называют возмущением)? Далее величины, относящиеся к невозмущённой задаче, будем писать с верхним индексом "(0)", то есть

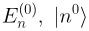
это собственные энергии и собственные состояния невозмущённой системы.

С помощью теории возмущений энергию системы после включения слабого взаимодействия (Eₙ без верхнего индекса "(0)") можно выразить через поправки к известным изначально собственным энергиям невозмущённой системы. Это исключительно математическая процедура, никак не привязанная к квантовой механике. Сначала запишем результат, а потом будем его интерпретировать:

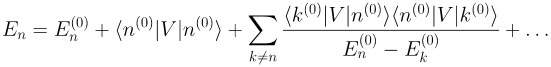
Ряд, вообще говоря, бесконечный и следующие его члены становятся прогрессивно сложнее, поэтому ограничимся только первыми тремя или, как ещё говорят, вторым порядком теории возмущений. Первое слагаемое в правой части это собственная энергия невозмущённой задачи. Этого и следовало ожидать: возмущение слабое, а значит новые энергии почти такие же, как и старые. Обратите внимание, что второе слагаемое пропорционально первой степени V, а третье — второй, этот паттерн сохранится и для следующих членов. Возведение малой величины в степень делает её ещё меньше, то есть следующие порядки теории возмущений будут вносить всё меньший вклад.

Теперь рассмотрим второй член. С математической точки зрения это просто какое-то число. Но, как написано в параграфе "обозначения", его можно понимать, как амплитуду вероятности процесса "состояние |n⁰> переходит в состояние |n⁰> (то есть в само себя) под воздействием V". Вот и первый виртуальный процесс: он бы не возник, если бы мы не применяли теорию возмущений и является результатом математических вычислений, но математическая формула допускает описанную физическую интерпретацию.

Третий член представляет собой сумму сам по себе. Для наглядности выпишем несколько её членов:

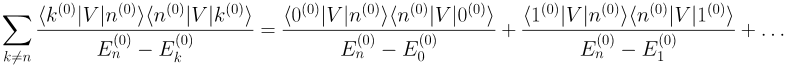
Как видно, в выражение входят амплитуды процессов "система из состояния |n> благодаря возмущению V перешла в состояния |0>, |1>... и вернулась обратно". Это тоже виртуальные процессы более высокого порядка. В следующих порядках виртуальные процессы будут становиться сложнее. Например, в третьем порядке появится слагаемое пропорциональное

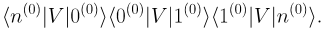
Его интерпретацию как виртуального процесса оставим в качестве упражнения для читателя.

Зачатки диаграмм Фейнмана

Знаменитые диаграммы Фейнмана тоже берут начало из теории возмущений. Каждая диаграмма соответствует члену из ряда теории возмущений и является своего рода мнемоническим правилом, позволяющим не запутаться при выписывании слагаемых высоких порядков.

На рисунке ниже я изобразил графически ряд из предыдущего параграфа для энергии E₀. Точки соответствуют состояниям невозмущённой задачи: нижняя точка — нулевое состояние, следующая за ней — первое и т.д. Стрелочки соответствуют виртуальным процессам <m|V|n>. Обратите внимание, что с увеличением порядка растёт количество виртуальных процессов, из уравнений это тоже следует. Практической пользы от моего рисунка мало, но он передаёт идею диаграмм Фейнмана.