Теория многоуровневой ранговой модуляции (Теоремы R.3-R.4)
Ilya Zelenskiy
Введение
Доказываем асимптотическую устойчивость оптимального распределения. Любые возмущения затухают со временем релаксации, а градиентный спуск - скорейший путь к равновесию.
Теорема R.3: Устойчивость равновесного состояния
Формулировка теоремы
Пусть задана ранговая структура системы R={1,2,…,N} с функцией ранговой стоимости g:R→R , где g(i)<g(i+1) для всех i∈{1,2,…,N−1} . Тогда оптимальное распределение
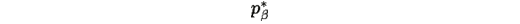
определенное в Теореме R.1, является глобально асимптотически устойчивой точкой динамической системы, заданной уравнением градиентного спуска:
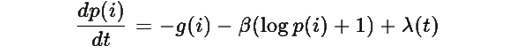
где λ(t) определяется из условия сохранения нормировки
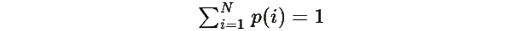
Предположения:
1. Начальное распределение
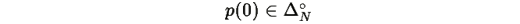
(внутренность симплекса, все компоненты строго положительны),
2. Параметр β>0 фиксирован (для параметрических версий требуется
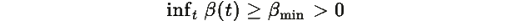
Более того, время релаксации к равновесию оценивается как:
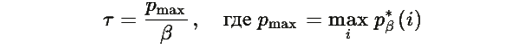
и для всех траекторий, начинающихся во внутренности симплекса, скорость сходимости удовлетворяет:
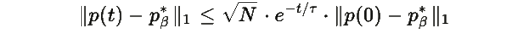
Замечание: Величина τ представляет собой оценку сверху времени релаксации; "реальное" время релаксации определяется как 1/λmin, где λmin — нижняя граница спектра симметризованной части матрицы Якоби.
Доказательство
1. Динамика системы с учетом нормировки
Рассмотрим систему дифференциальных уравнений:
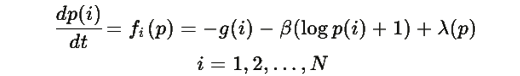
где λ(p) определяется из условия нормировки
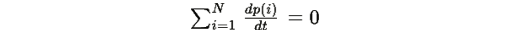
получаем:
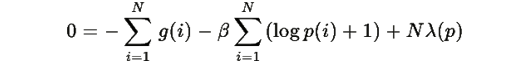
Отсюда:
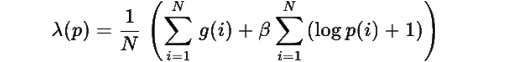
Подставляя обратно, получаем замкнутую систему:
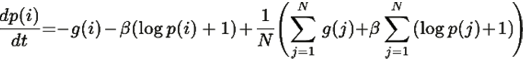
2. Функция Ляпунова и глобальная устойчивость
Рассмотрим функционал
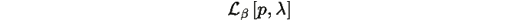
из Определения R.5:
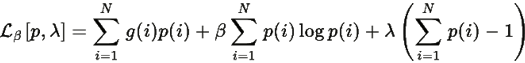
Вычислим его производную вдоль траектории системы:
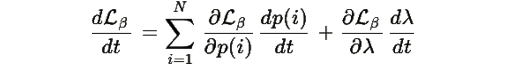
Поскольку
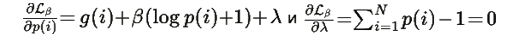
(в силу нормировки), получаем:
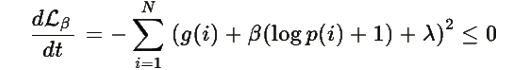
Равенство достигается только когда g(i)+β(log p(i)+1)+λ=0 для всех i , то есть в точке равновесия
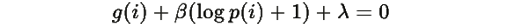
Замечание о глобальной устойчивости: Поскольку
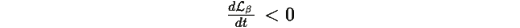
вдоль любой нетривиальной траектории, множество
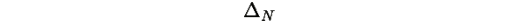
компактно, и
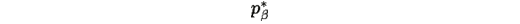
единственная стационарная точка (по Теореме R.1), по теореме ЛаСалла траектории сходятся к
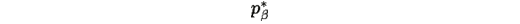
из любой начальной точки
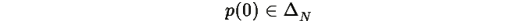
Вывод:
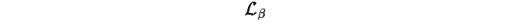
является функцией Ляпунова для нашей системы, и равновесие
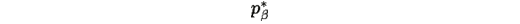
глобально асимптотически устойчиво.
3. Инвариантность внутренности симплекса
Замечание: Если начальное распределение p(0) лежит во внутренности симплекса
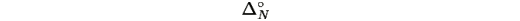
т.е.
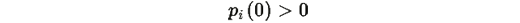
для всех i, то траектория остается внутри
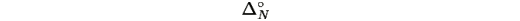
для всех t>0.
Обоснование: При
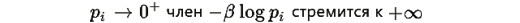
поэтому векторное поле "толкает" компоненту внутрь симплекса. Это гарантирует, что
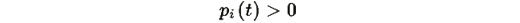
для всех t>0 и i, что делает логарифмы в системе корректно определенными и позволяет применять линеаризацию вблизи равновесия.
Примечание: Для начальных условий на границе симплекса
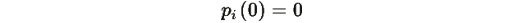
требуется рассмотрение слабых решений или введение отражающих границ, что выходит за рамки данной работы.
4. Линеаризация в окрестности равновесия
Рассмотрим малое возмущение вокруг равновесия:
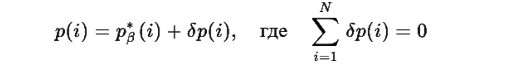
Обозначим правую часть уравнения как:
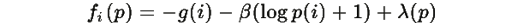
где
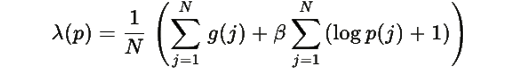
Вычислим частные производные (предполагая p(i)>0 ):
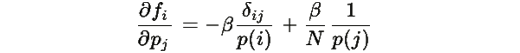
В точке равновесия
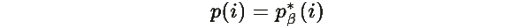
линеаризованная система имеет вид:
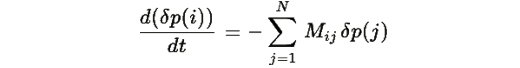
где матрица M имеет элементы:
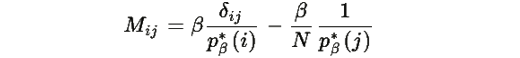
Замечание: Матрица M не обязательно симметрична
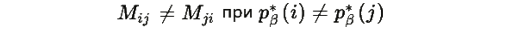
но мы покажем, что квадратичная форма
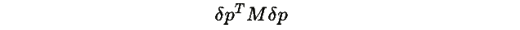
положительна на подпространстве
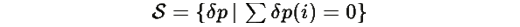
5. Положительная определенность квадратичной формы
Рассмотрим квадратичную форму для любого
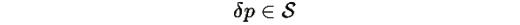
Подставляя элементы M(i, j):
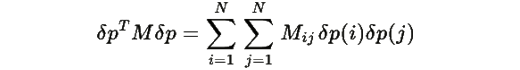
Перегруппируем второе слагаемое:
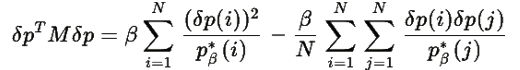
Поскольку
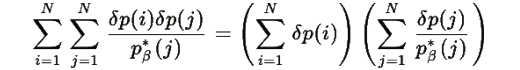
поскольку
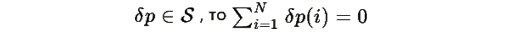
и второе слагаемое равно нулю. Следовательно:
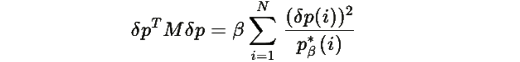
Так как
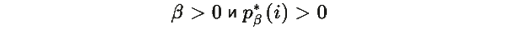
для всех i (по Теореме R.1), то:
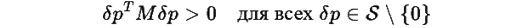
Таким образом, квадратичная форма положительно определена на S.
6. Оценка скорости затухания возмущений
Для любого
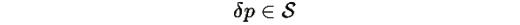
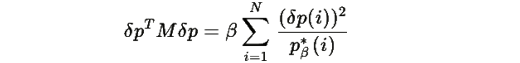
Пусть
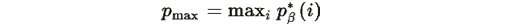
Тогда для всех i:
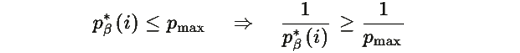
Следовательно:
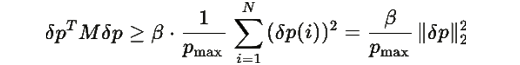
По определению, минимальное значение квадратичной формы:
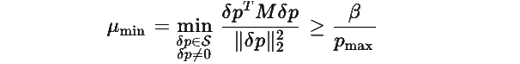
Замечание: Поскольку матрица M не симметрична,
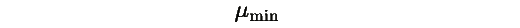
здесь обозначает минимальное значение квадратичной формы (а не минимальное собственное значение). Это дает нижнюю спектральную границу для симметризованной части матрицы M и достаточную оценку скорости экспоненциального затухания.
7. Оценка времени релаксации
Из линеаризованной системы следует, что для достаточно малых возмущений
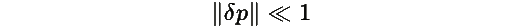
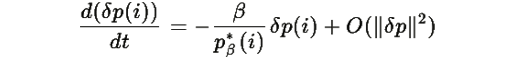
Для малых начальных возмущений линейная оценка доминирует, и:
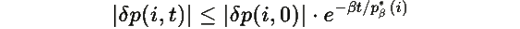
Так как
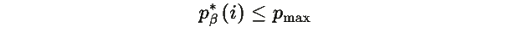
для всех i , то:
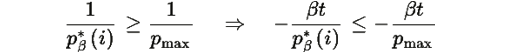
Следовательно:
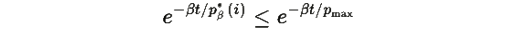
Поэтому:
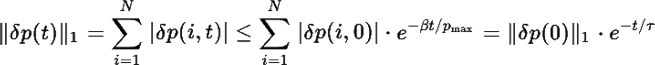
где
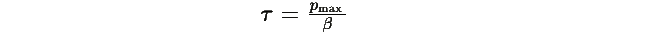
Окончательная оценка: Используя стандартные неравенства для норм
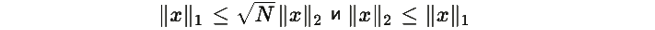
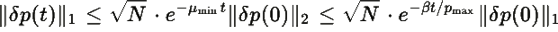
Замечания:
1. Это компонентная оценка, получаемая из линеаризованной диагональной части. Для формальной строгости можно использовать матричный экспоненциальный метод или неравенство Грёнволя, что дает тот же показатель экспоненциального затухания с незначительно отличающимися константами.
2. Формула
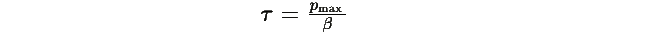
дает консервативную оценку времени релаксации сверху. Более точная величина связана с реальным спектром оператора линеаризации (симметризованной части).
8. Связь с принципом скорейшего спуска
Рассмотрим функционал "времени достижения равновесия":
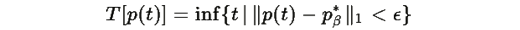
Пусть q(t) — произвольная траектория с теми же начальными условиями и условием
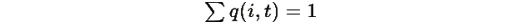
Тогда:
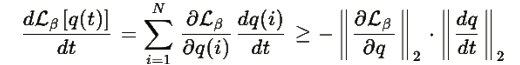
По неравенству Коши-Шварца, равенство достигается когда
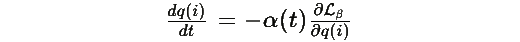
для некоторого α(t)>0 . Более строго, рассмотрим функционал:
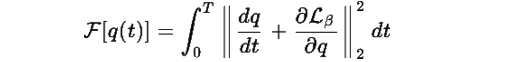
Минимум
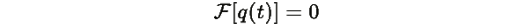
достигается только при
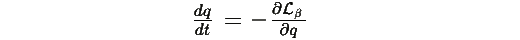
то есть при градиентном спуске.
Вывод: Градиентный спуск обеспечивает скорейший спуск к равновесию.
Заключение доказательства
1. Функционал
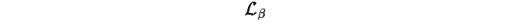
является функцией Ляпунова, и равновесие
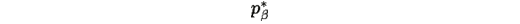
глобально асимптотически устойчиво,
2. Линеаризация в окрестности равновесия показывает, что квадратичная форма
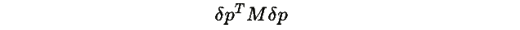
положительно определена на подпространстве S,
3. Минимальное значение квадратичной формы
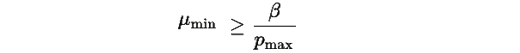
где
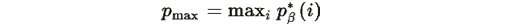
3. Для траекторий, начинающихся во внутренности симплекса, время релаксации оценивается как
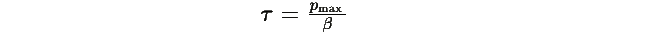
4. Градиентный спуск обеспечивает скорейший спуск к равновесию.
Таким образом, Теорема R.3 доказана. ■
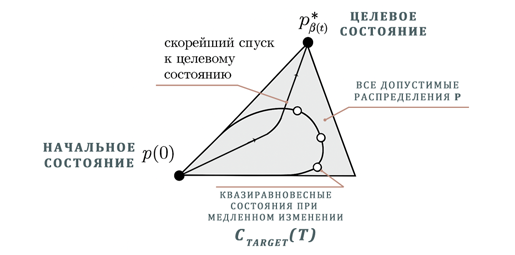
Теорема R.4: Параметрическая динамика и переходы между состояниями
Формулировка теоремы
Пусть задана ранговая структура системы R={1,2,…,N} с функцией ранговой стоимости g:R→R , где g(i)<g(i+1) для всех i∈{1,2,…,N−1} . Рассмотрим динамическую систему, заданную системой уравнений:
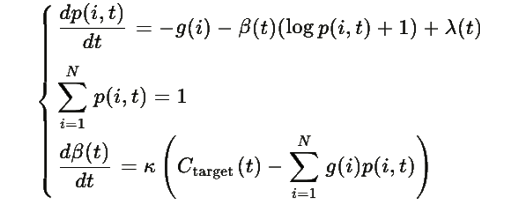
где κ>0 — скорость адаптации, Ctarget(t) — целевое значение средней стоимости, а λ(t) определяется из условия сохранения нормировки.
Предположения:
1. Начальное распределение
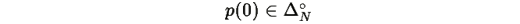
(внутренность симплекса, все компоненты строго положительны),
2. нижняя граница для β
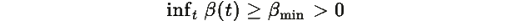
3. Ctarget(t) — гладкая функция времени.
Тогда:
1. Для любого начального состояния (p(0),β(0)) траектория системы стремится к состоянию, где
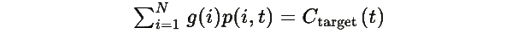
2. При медленном изменении Ctarget(t) система остается близкой к квазиравновесному состоянию
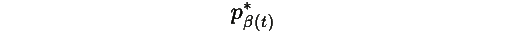
где
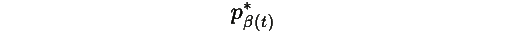
оптимальное распределение из Теоремы R.1,
3. Переход между состояниями соответствует принципу скорейшего спуска, минимизируя функционал:
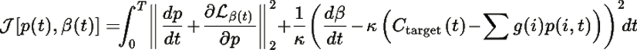
Доказательство
1. Существование и устойчивость целевого состояния
Утверждение 1.1: Функция
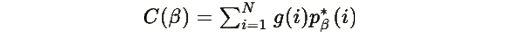
строго возрастает по β.
Доказательство:
Из Теоремы R.1,
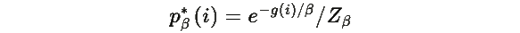
Вычислим производную:
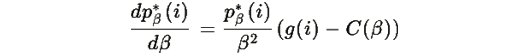
где
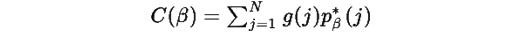
Тогда:
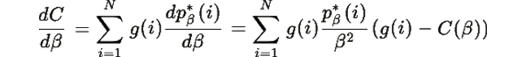
Перегруппируем:
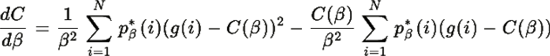
Вторая сумма равна нулю (по определению C(β) ), поэтому:
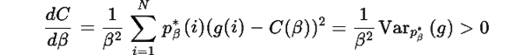
где
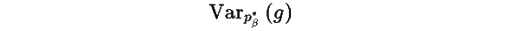
дисперсия g(i) относительно распределения
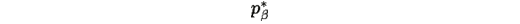
Так как g(i) не постоянна (по условию g(i)<g(i+1) ), дисперсия строго положительна, поэтому
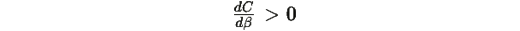
Следовательно, C(β) строго возрастает по β, что означает, что для любого Ctarget существует единственный
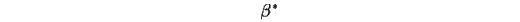
такой, что
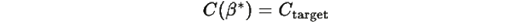
Утверждение 1.2: Функционал
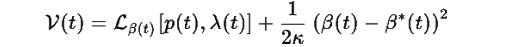
где
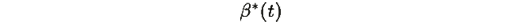
значение β, для которого
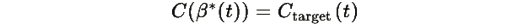
является функцией Ляпунова, и
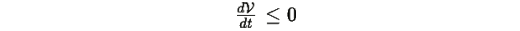
Доказательство:
Сначала вычислим производную L
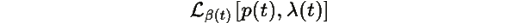
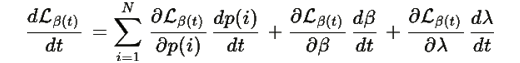
Как и в Теореме R.3,
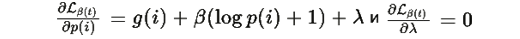
(в силу нормировки), поэтому:
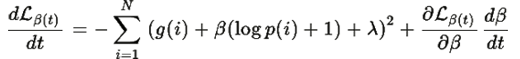
Вычислим
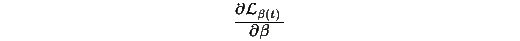
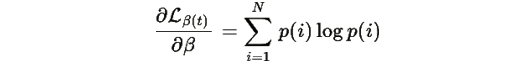
Теперь вычислим производную второго члена:
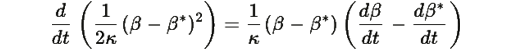
Из третьего уравнения системы:
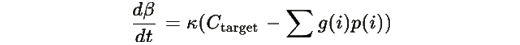
По определению
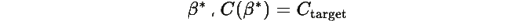
Используя разложение в ряд Тейлора:
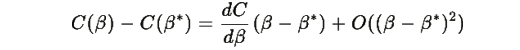
Следовательно:
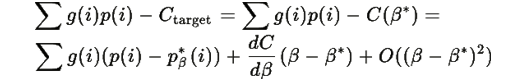
В окрестности равновесия
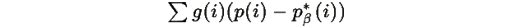
мало, поэтому приближенно:
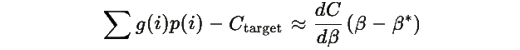
Следовательно:
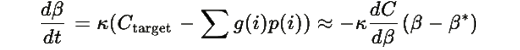
Теперь объединим все части:
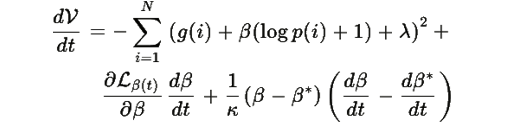
Подставляя
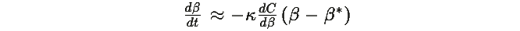
и обозначая
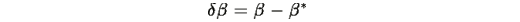
получаем:
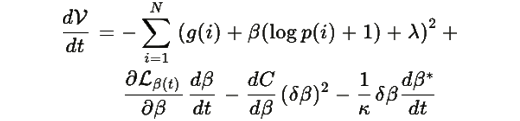
При медленном изменении
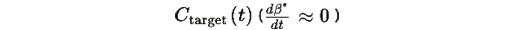
и учитывая, что
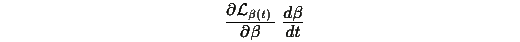
ограничено, получаем:
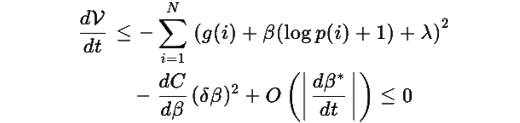
при достаточно медленном изменении Ctarget(t).
Равенство достигается только когда
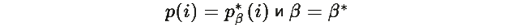
Вывод: V(t) является функцией Ляпунова, и система стремится к состоянию, где
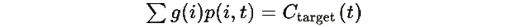
2. Квазиадиабатическое приближение
Утверждение 2.1: При медленном изменении Ctarget(t) система остается близкой к квазиравновесному состоянию
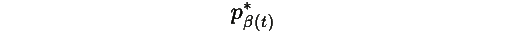
Доказательство:
Определим отклонение от квазиравновесия:
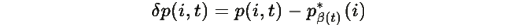
Из уравнения динамики:
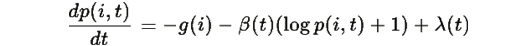
Для квазиравновесного состояния:
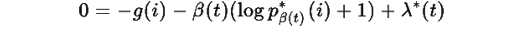
где
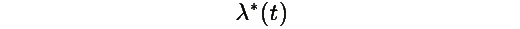
соответствует нормировке
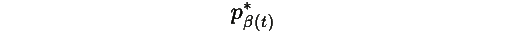
Вычитая эти уравнения и линеаризуя по δp, получаем:
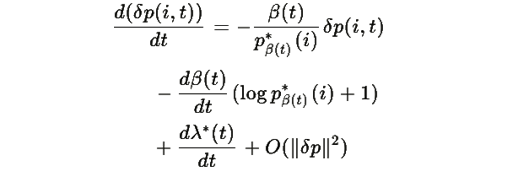
Это линейное дифференциальное уравнение с решением:
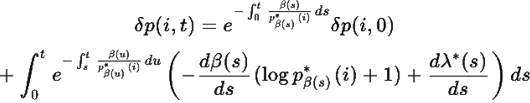
Из Теоремы R.3, время релаксации
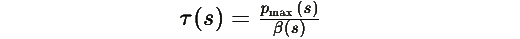
где
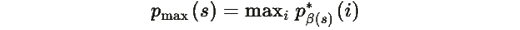
поэтому:
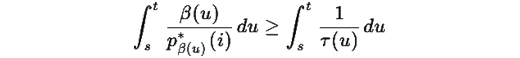
Поскольку
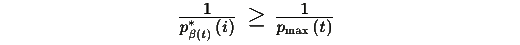
где
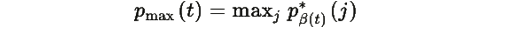
то:
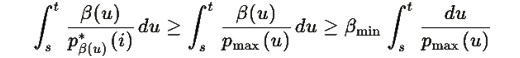
где
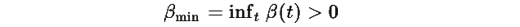
Если
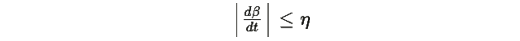
для некоторой малой константы η, и
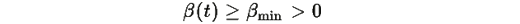
то:
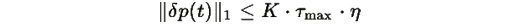
где K — константа, зависящая от βmin и N, а τmax — максимальное время релаксации.
Вывод: При медленном изменении β(t) (η мало) система остается близкой к квазиравновесному состоянию
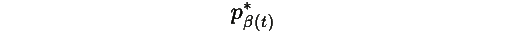
3. Скорость перехода между состояниями
Утверждение 3.1: Динамика системы минимизирует функционал J[p(t),β(t)]
Доказательство:
Рассмотрим вариацию функционала:
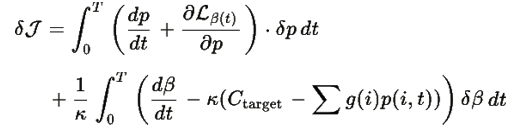
Минимум достигается когда:
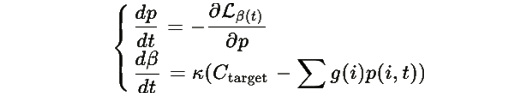
то есть именно при нашей динамике.
Более строго, функционал J[p(t),β(t)] можно записать как:
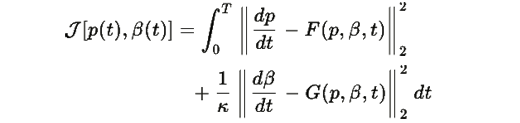
где
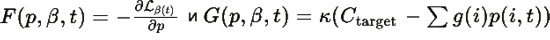
Этот функционал достигает минимума 0 только на траекториях, удовлетворяющих системе уравнений:
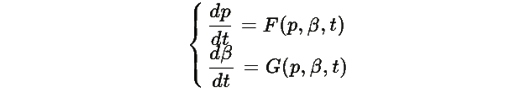
Вывод: Наша динамика обеспечивает скорейший спуск к целевому состоянию в смысле минимизации J[p(t),β(t)]. □
4. Оценка времени перехода
Утверждение 4.1: Время перехода между состояниями конечное и оценивается как:
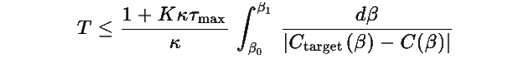
где Ctarget(β) — целевая стоимость как функция β.
Доказательство
При переходе от β0 к β1 время перехода можно оценить как:
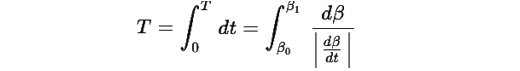
Из третьего уравнения системы:
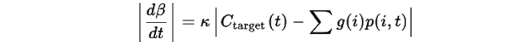
В квазиадиабатическом приближении:
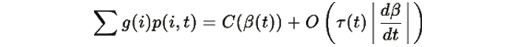
поэтому:
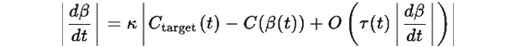
Предполагая, что
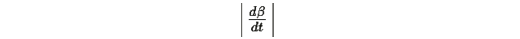
ограничено, получаем:
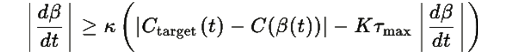
для некоторой константы K.
Следовательно:
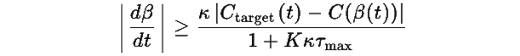
Поэтому:
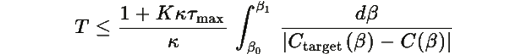
Вывод: Время перехода между состояниями конечное и зависит от скорости адаптации κ и времени релаксации τmax. □
Заключение доказательства
1. Функционал V(t) является функцией Ляпунова, доказывающей стремление системы к состоянию с целевой средней стоимостью,
2. При медленном изменении Ctarget(t) система остается близкой к квазиравновесному состоянию
3. Динамика системы минимизирует функционал J[p(t),β(t)] , обеспечивая скорейший спуск к целевому состоянию,
5. Время перехода между состояниями конечное и зависит от скорости адаптации κ и времени релаксации.
Таким образом, Теорема R.4 доказана. ■