TREX: 27-ричная симметричная система счисления

Каждый специалист по компьютерам знает, насколько сложно работать с длинными последовательностями нулей и единиц. На помощь ему приходят восьмеричная и шестнадцатиричная системы счисления, обеспечивающие более компактное представление информации.

С троичной системой счисления ситуация хуже: есть несколько способов представления троичных чисел и есть несколько способов компактной записи троичных чисел, но они имеют недостатки, усложняющие работу с ними.

Система кодирования TREX разработана для компактного отображения симметричной троичной системы счисления при ее использовании в компьютерных системах

Замечания

1. В данной статье речь идет только о симметричной троичной системе счисления, использующей значения {-1, 0, +1}.
2. Недостатки предлагаемых на сегодняшний момент 9-ти и 27-ричных систем кодирования троичных чисел будут упомянуты ниже в сравнении с системой TREX.

Проблематика

1. При разработке ПО для работы с троичными компьютерами встает вопрос вывода информации на различные устройства отображения информации. При этом информация должна выводиться упорядоченно, чтобы при печати, например, дампов одинаковые разряды чисел располагались на одинаковых позиция строки.
2. Работа с троичной логикой очень непривычна даже для опытных программистов, поэтому для повышения удобства работы, минимизации человеческих ошибок и сокращения времени освоения троичного компьютера (который когда-нибудь уже будет создан) требуется система кодирования, обладающая простотой, наглядностью и односимвольностью ( отображением одного разряда одним символом, желательно из стандартного набора ASCII)

Представление троичных чисел

Для записи симметричной троичной системы счисления удобной формы отображения на экране компьютера можно добиться, используя алфавит {-, 0, +}.

Пример:

+-0-0+++- -++0+00--

000+-+--0 +-+-+-++0

-0+0-+00+ 0-0+++--0

Компактное представление троичных чисел

Поскольку с длинными последовательностями знаков «-», «0» и «+» работать неудобно (как и с длинными последовательностями «0» и «1» в двоичной системе счисления), то должна быть возможность компактного отображения информации (по аналогии с HEX-кодом).

По аналогии с названием HEX, для представляемой системы счисления предлагается использовать название TREX.

Описание системы кодирования

Система TREX использует следующий алфавит:

{ m..a, 0, A..M}

Используется следующая схема кодирования:

Десятичное Троичное TREX

значение  значение

-13     ---    m

-12     --0    l

-11     --+    k

-10     -0-    j

 -9     -00    i

 -8     -0+    h

 -7     -+-    g

 -6     -+0    f

 -5     -++    e

 -4     0--    d

 -3     0-0    c

 -2     0-+    b

 -1     00-    a

 0     000    0

 +1     00+    A

 +2     0+-    B

 +3     0+0    C

 +4     0++    D

 +5     +--    E

 +6     +-0    F

 +7     +-+    G

 +8     +0-    H

 +9     +00    I

+10     +0+    J

+11     ++-    K

+12     ++0    L

+13     +++    M

Троичные единицы данных и их запись в TREX

Трит

Единичный троичный разряд, который в симметричной троичной системе счисления может принимать значения {-1, 0, +1}. Для удобного отображения на устройствах вывода информации целесообразно использовать символы {-, 0, +} соответственно.

Пример:

Троичная система счисления Десятичное значение

    +           +1

     0            0

     -           -1

Трибл

Трибл (3 троичных разряда или 1/3 часть трайта) кодируется одним символом TREX

Пример:

M = +++

Трайт

При использовании системы TREX предлагается трайтом называть девять троичных разрядов в отличие от применяемого в вычислительных машинах «Сетунь» 6-ти разрядного трайта. Девятиразрядный трайт достаточно велик, чтобы закодировать алфавит, включающий цифры, математические и служебные знаки, заглавные и строчные буквы для многих языков. Диапазон значений трайта от -9841 до +9841. В трайте целое число 27-ричных цифр (триблов). Трайт кодируется тремя символами TREX

Пример:

A0m = 00+ 000 ---

Преимущества перед имеющимися 9-ти и 27-ричными системами кодирования

Предлагаемая система кодирования выгодно отличается от предлагавшихся до этого 9-ти и 27-ричных систем следующими особенностями:

• односимвольностью — каждое значение отображается одним символом, не требуется вводить двухсимвольные обозначения.
• 
  
• Существующие системы кодирования:
• существует 9-ричная система, использующая алфавит {-4,-3,-2,-1,0,1,2,3,4}
• естественностью – для записи не применяются специальные символы.
• 
  
• Существующие системы кодирования:
• существует вариант 9-тиричной системы счисления, использующий специальные символы с верхней чертой (не знаю, как нарисовать символы с верхним подчеркиванием, поэтому вставил картинку):

• 
  
• 
  
• 
  
• 
  
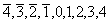
• Свойства односимвольности и естественности очень удобны при компактном отображении на экране троичных дампов без использования специальных шрифтов.
• 
  
• Пример:
• двухсимвольная   система
• запись       TREX
• (столбцы «ползут») (столбцы ровные)
• -4 1 0 -2 -3    A a 0 B B
• 0 0 0 1 -2     M M m d d
• 1 1 -3 0 0     C c a d d
• визуальной симметричностью — для противоположных значений используются одни и те же символы с разным регистром, в отличие от систем, где противоположные значения обозначаются разными символами.
• 
  
• Существующие системы кодирования:
• существуют 9-ричная система, использующая алфавит {W,X,Y,Z,0,1,2,3,4}, и 27-ричная система, использующая алфавит {0,A..Z}).
• Свойство визуальной симметричности позволяет выполнять очевидные операции с троичными числами «в уме»
• Пример:
• A = -a
• MMM + mmm = 0
• наглядностью - возможностью в уме выполнять следующие простейшие операции с числами:
• определение знака числа — по регистру самой старшей цифры.
• 
  
• Пример:
• Akm > 0
• mmD < 0
• инверсия числа - производится сменой регистра всех символов.
• 
  
• Пример:
• -(AdFGhb) = aDfgHB
• вычисление модуля числа – модуль числа равен самому числу, если старшая цифра положительная или инвертированному числу, если она отрицательная
• 
  
• Пример:
• mod (Mf0) = Mf0
• mod (a0H) = A0h
• упрощение при сложении - при сложении длинных чисел одинаковые символы различных регистров, находящиеся в одинаковых разрядах можно сократить
• 
  
• Пример:
•  Mfa    00a
• +   => +    => 00G
• mFH    00H
• сравнение по первой отличающейся цифре - при сравнении двух чисел, как положительных, так и отрицательных, больше то число, у которого больше первая отличающаяся цифра, начиная со старшей значащей.
• 
  
• Пример:
• Mfa > Mma
• afa > bfa

Выводы

Предлагаемая система кодирования позволит:

1. упорядочить отображение троичной информации на экране компьютера (выровненные дампы)
2. уменьшить число выводимых знаков по сравнению с поразрядным выводом троичных данных
3. облегчить работу с троичными числами широкому кругу специалистов
4. уменьшить количество ошибок при разработке программного обеспечения для троичных компьютеров или их эмуляторов.