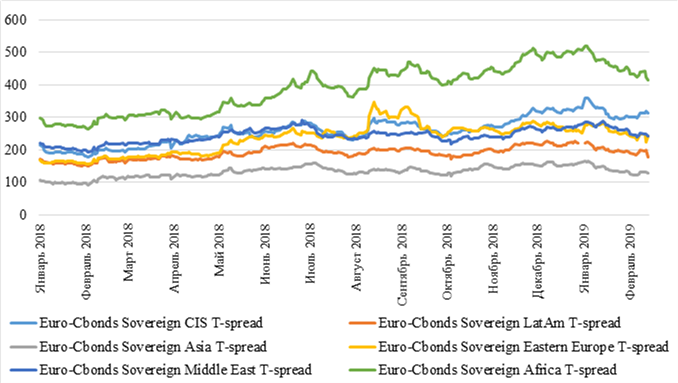
T Spread

🔞 ALL INFORMATION CLICK HERE 👈🏻👈🏻👈🏻
T Spread
From Wikipedia, the free encyclopedia
The TED spread is the difference between the interest rates on interbank loans and on short-term U.S. government debt ("T-bills"). TED is an acronym formed from T-Bill and ED , the ticker symbol for the Eurodollar futures contract.
Initially, the TED spread was the difference between the interest rates for three-month U.S. Treasuries contracts and the three-month Eurodollars contract as represented by the London Interbank Offered Rate (LIBOR). However, since the Chicago Mercantile Exchange dropped T-bill futures after the 1987 crash, [1] the TED spread is now calculated as the difference between the three-month LIBOR and the three-month T-bill interest rate.
The size of the spread is usually denominated in basis points (bps). For example, if the T-bill rate is 5.10% and ED trades at 5.50%, the TED spread is 40 bps. The TED spread fluctuates over time but generally has remained within the range of 10 and 50 bps (0.1% and 0.5%) except in times of financial crisis. A rising TED spread often presages a downturn in the U.S. stock market, as it indicates that liquidity is being withdrawn.
The TED spread is an indicator of perceived credit risk in the general economy, [2] since T-bills are considered risk-free while LIBOR reflects the credit risk of lending to commercial banks. An increase in the TED spread is a sign that lenders believe the risk of default on interbank loans (also known as counterparty risk ) is increasing. Interbank lenders, therefore, demand a higher rate of interest, or accept lower returns on safe investments such as T-bills. When the risk of bank defaults is considered to be decreasing, the TED spread decreases. [3] Boudt, Paulus, and Rosenthal show that a TED spread above 48 basis points is indicative of economic crisis. [4]
The long-term average of the TED spread has been 30 basis points with a maximum of 50 bps. During 2007, the subprime mortgage crisis ballooned the TED spread to a region of 150–200 bps. On September 17, 2008, the TED spread exceeded 300 bps, breaking the previous record set after the Black Monday crash of 1987. [5] Some higher readings for the spread were due to inability to obtain accurate LIBOR rates in the absence of a liquid unsecured lending market. [6] On October 10, 2008, the TED spread reached another new high of 457 basis points.
In October 2013, due to worries regarding a potential default on US debt, the 1-month TED went negative for the first time since it started being tracked. [7] [8]
TED Spread Definition
TED spread - Wikipedia
(PDF) t - spread strongly stable monomial ideals
Credit spread (options) - Wikipedia
t - spread - Russian translation – Linguee
Preprints and early-stage research may not have been peer reviewed yet.
We introduce the concept of $t$-spread monomials and $t$-spread strongly stable ideals. These concepts are a natural generalization of strongly stable and squarefree strongly stable ideals. For the study of this class of ideals we use the $t$-fold stretching operator. It is shown that $t$-spread strongly stable ideals are componentwise linear. Their height, their graded Betti numbers and their generic initial ideal are determined. We also consider the toric rings whose generators come from $t$-spread principal Borel ideals.
Content may be subject to copyright.
arXiv:1805.02368v1 [math.AC] 7 May 2018
T-SPREAD STRONGL Y ST ABLE MONOMIAL IDEALS
URGEN HERZOG, A YESHA ASLOOB QURESHI
Abstract. W e introduce the concept of t -s pread monomials and t -spread strongly
stable ideals. These concepts are a natural generaliza tion of strongly stable and
squarefree strongly stable ideals. F or the study of this class of ideals we use the
t -fold stretching operator. It is shown that t -spread strongly stable ideals are
componentwise linear. Their height, their graded Betti numbers and their generic
initial ideal are determined. W e also co nsider the toric rings whose generators
come from t -spread principal Bor el ideals.
Among the monomial ideals, the squarefree monomial ideals play a distinguished
role as they are linked in many ways to combi natorial ob jects suc h as simplicial
complexes and graphs. Squarefree monomials in a p olynomial ring K [ x 1 ,...,x n ]
which generate these ideals are monomials of the form x i 1 . . . x i d with i 1 < i 2 <
··· < i d . In this paper, we call a monomial x i 1 x i 2 ··· x i d with i 1 ≤ i 2 ≤ · · · ≤ i d
t -spre ad, if i j − i j − 1 ≥ t for 2 ≤ j ≤ n . Note that, any monomial is 0-spread, while
the squarefree monomials are 1-spread.
A monomial ideal in S is called a t -spread monomial ide al , if it is generated
by t -spread monomials. For example, I = ( x 1 x 4 x 8 , x 2 x 5 x 8 , x 1 x 5 x 9 , x 2 x 6 x 9 , x 4 x 9 ) ⊂
K [ x 1 ,...,x 9 ] is a 3-spread monomial ideal, but not 4-spread, because x 2 x 5 x 8 is not
a 4-spread monomial. Note that 2–spread monomial ideals appear as initial ideals
for the defining ideals of the fiber cones of monomial ideals in two v ariables [4].
There is a w ell-known deformation, called polarization, which assigns to each
monomial ideal a squarefree monomial ideal, preserving all homological properties
of these ideals. In this way , many problems regarding monomial ideals can be
reduced to the study of squarefree monomial ideals. On the other hand, in shifting
theory , in particular for symmetric alg ebraic shifting, one used another operator,
called stretching op erator , see [10], [3]. To transform an arbitrary monomial u =
x i 1 ··· x i d with i 1 ≤ i 2 ≤ · · · ≤ i d into a squarefree monomial, one defines the
stretched monomial σ ( u ) = x i 1 x i 2 +1 x i 3 +2 . . . x i d +( d − 1) . Let I be a monomial ideal
and G ( I ) = { u 1 ,...,u m } b e the unique minimal monomial set of generators o f I .
Then I σ is defined to be the ideal with G ( I σ ) = { σ ( u 1 ) ,...,σ ( u m ) } .
2010 Mathematics Subject Classific ation. 05E40, 13C1 4, 13D02.
Key wor ds and phrases. Strongly stable ideals, stretching op erator, Betti num bers , Alexander
Part of this paper was written while the second author visited F aculty of Engineering and
Natural Sciences at Sabanci University .
In this paper we study resolutions which arise as iterated mapping cones.
In this paper we consider some subalgebras of the d-th Veronese subring of a polynomial ring, generated by stable subsets of monomials. We prove that these algebras are Koszul, showing that the presentation ideals have Gröbner bases of quadrics with respect to suitable term orders. Since the initial monomials of the elements of these Gröbner bases are square- free, it follows by a result of STURMFELS [S, 13.15], that the algebras under consideration are normal, and thus Cohen-Macaulay.
Algebraic shifting is a correspondence which associates to a simplicial complex K another simplicial complex (K) of a special type. In fact, there are two main variants based on symmetric algebra and on exterior algebra, respectively. The construction is algebraic and is closely related to "Gröbner bases" and specifically to "generic initial ideals" in commutative algebra. Algebraic shifting preserves various combinatorial and topological properties of K, while others disappear. Thus, for example, (K) has the same Betti numbers as those of K while the ring structure on cohomology is destroyed as (K) is always a wedge of spheres. One of the important challenges is to deepen the relation between algebraic shifting and basic notions and constructions of algebraic topology. Some important progress in this direction was achieved by Duval. Algebraic shifting also preserves the property of K being CohenMacaulay. The front-line of our knowledge in this direction is a farreachi...
Monomial ideals, Grad. Texts in Math
J. Herzog, T. Hibi, Monomial ideals, Grad. Texts in Math. 260, Springer, London, 2010.
J Herzog A Qureshi M Mohammadi Saem
J. Herzog, A. Asloob Qureshi, M. Mohammadi Saem, The fiber cone of a monomial ideal in
two variables, arXiv:1711.08775.
By it's name this bicycle Rechargeable by Dynamo. and Folding also electric. this is Nature Friendly Concept.
December 1984 · Journal of Structural Geology
The relative deformation gradient is defined and used to compare deformations between any two points of a body. This concept is useful in the geometrical analysis of deformation in natural folds, where only deformed planes and straight lines can be observed. The case of cylindrical folds with deformed lineations is studied.
Ce travail de thèse répond à une demande du Centre de formation par apprentissage ingénieur 2000. Il s'agit de proposer, dans le cas d'une formation d'ingénieurs en alternance, des principes pour construire des activités académiques articulées aux activités industrielles. Nous avons alors choisi une approche didactique qui se centre sur l'activité de formation de l'apprenti ingénieur. Nous avons ... [Show full abstract] mis en évidence la nature des savoirs mobilisés dans des activités de conception dans les deux séquences de formation : ces savoirs sont fortement déterminés par la situation de l'activité en tant que complexe de conditions et de contraintes humaines, organisationnelles et matérielles. Par ailleurs nous avons montré que, quelle que soit la séquence de formation considérée (industrielle ou académique), l'activité de conception est définie par quatre caractères essentiels : la visée, la situation, les savoirs mobilisés et les modalités de mobilisation des savoirs. Les ruptures entre les activités de conception dans les deux séquences de la formation en alternance relativement à ces qutare caractères ont notamment été dégagées. Enfin, nous avons étudié les difficultés des apprentis à utiliser une assistance pédagogique en ligne et valider un carnet de bord en tant qu'outils permettant d'opérer des continuités, entre les activités de conception industrielles et académiques
August 2019 · Communications in Algebra
We introduce the concept of t-spread monomials and t-spread strongly stable ideals. These concepts are a natural generalization of strongly stable and squarefree strongly stable ideals. For the study of this class of ideals we use the t-fold stretching operator. It is shown that t-spread strongly stable ideals are componentwise linear. Their height, their graded Betti numbers and their generic ... [Show full abstract] initial ideal are determined. We also consider the toric rings whose generators come from t-spread principal Borel ideals.
March 2014 · Mathematische Nachrichten
We introduce balanced polyominoes and show that their ideal of inner minors
is a prime ideal and has a quadratic Gr\"obner basis with respect to any
monomial order, and we show that any row or column convex and any tree-like
polyomino is simple and balanced.
October 2013 · Proceedings of the American Mathematical Society
In this paper, we introduced the polarization of Koszul cycles and use it to
study the depth function of powers of edge ideals of whisker graphs.
We introduce pseudo-Gorenstein rings and characterize those Hibi rings
attached to a finite distributive lattice L which are pseudo-Gorenstein. The
characterization is given in terms of the poset of join-irreducible elements of
L. We also present a necessary condition for Hibi rings to be level. Special
attention is given to planar and hyper-planar lattices. Finally the
pseudo-Goresntein and ... [Show full abstract] level property of Hibi rings and generalized Hibi rings
is compared with each other.
© 2008-2021 ResearchGate GmbH. All rights reserved.
Aletta Ocean Massage Sex
Young Mom Sleep Sex Video
Double Penetration Slamming
Yanka Meirelles Evil Angel
Sexy Lingerie Porno