Сжатие сетей

С каждый годом нейронные сети становятся все больше, приложений, в которых их можно их применять - тоже, эффективность вычислительных ресурсов и память на устройствах не поспевает за этим взрывом. Сети AlexNet, VGG-16 and Resnet-18 занимают сотни мегабайт, а для многих задач (например, AR, VR, text2speech) хочется иметь возможность real-time применения сетей на мобильных устройствах. Сокращать размеры сетей - даже более актуальная на текущий момент задача, чем делать новые огромные архитектуры. Ниже мы познакомимся с основными способами сокращать размеры сетей.

Бинаризация и квантизация сетей.

Простой сценарий - мы просто округляем параметры нейронных сетей с 64 бит до 32 бит. Получается не очень большая разница в метриках. Но если мы хотим из числа на 64 бита делать бинарную величину (или величину, принимающую небольшое количество значений), такая стратегия больше не прокатит. Где выход?

На помощь нам приходит алгоритм BinaryConnect. Шаги алгоритма:

1) Берем обычную сеть с непрерывными весами, рассчитываем новые дискретные веса - берем знаки непрерывных весов

2) Делаем inference и backprop, получаем антиградиенты по дискретным весам (непрерывные значения)

3) Вычитаем непрерывные антиградиенты из непрерывных весов, получаем новые непрерывные веса

4) Повторяем

Недостаток метода: когда мы бинаризуем непрерывные веса, мы делаем это достаточно тупо - берем знак непрерывного веса. Можно сделать сложней: выучить функцию, которой можно получать дискретное значение веса из непрерывного. Для этого, вместо того, чтобы минимизировать обычную функцию потерь, будем оптимизировать сумму функции потерь и оператор, который равен нулю, если веса дискретны, и равен бесконечности - если нет. Оптимизация негладкого функционала - вещь больная, но поскольку стандартная функция потерь - выпуклая и гладкая, а оператор - выпуклый и негладкий, можно применить алгоритм Ньютона, который итеративно находит параметры, минимизирующие такой функционал (выпуклая и гладкая функция + выпуклая функция).

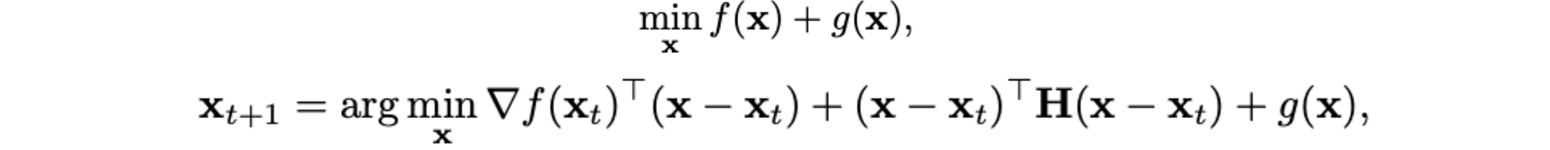
Pruning весов

Суть pruning в том, чтобы убрать из сети неинформативные параметры, тем самым облегчив ее, и упростить вычисления. Самая интуитивная идея - итеративно убирать параметры с маленькими значениями. Но кажется, это очень простое приближение, не учитывающее влияние значения каждого конкретного параметра на финальную функцию потерь. Эта проблема решается в известной статье Яна Лекуна Optimal Brain Damage. Суть заключается в следующем - сначала мы тренируем сеть до сходимости, затем выкидываем 'незначимые' по нашей метрике параметры, затем заново обучаем сеть до сходимости и так далее. Можно расписать то, как изменение каждого параметра в сети повлияет на функцию потерь через первые и вторые производные:

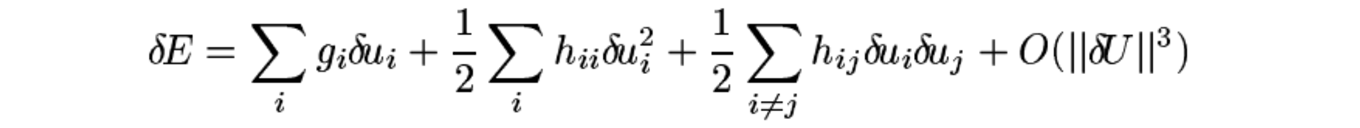
Авторы забивают на первый член, поскольку мы натренировали сеть до какого-то локального или глобального минимума, соответственно первая производная обращается в ноль. Также забиваем на третий член - считаем, что удаление параметров независимо и совместно даст одинаковый эффект. Константу мы тоже убираем, так как считаем, что квадратичной аппроксимации достаточно.

В итоге остается второй член. Соответственно значимость параметра, по которой мы будем принимать решение об удалении параметра из сети, мы считаем умножением квадрата параметра на вторую производную функции потерь по этому параметру.

Sharing весов

Можно подойти к вопросу уменьшения похожим на pruning образом, но немного с другой стороны - выбирать группы параметров, и заменять их одним параметром. Это и делают с помощью hashing trick авторы в статье Compressing Neural Networks with the Hashing Trick. Hashink trick - это такой прием для ускорения, когда, чтобы получить вектор для какого нибудь объекта (например, слова), не нужно искать его в словаре или искать его индекс в таблице. Достаточно применить к признаку hash-функцию, которая умеет выдавать уникальные числа от 0 до размерности словаря - полученный результат и будет индексом, по которому уже в отсортированном массиве (не в словаре), нужно искать признаки. Авторы выделяют группы параметров, однако хранят в памяти только один общий вес для каждой группы. Эффективно и быстро узнать, какие параметры соответствуют той или иной группе, можно, применив hashing trick.

Структурирование матриц преобразования

Один полносвязный слой - это операция умножения данных на матрицу преобразования. Матрица преобразования D хранит в себе n x m параметров, где n - размер входного представления, а m - размер выходного представления. Можно заменить матрицу D на новую, более оптимальную матрицу R и потребовать от матрицы преобразования R ряд свойств, чтобы упростить себе жизнь, придав ей тем самым определенную структуру:

1) Параметры, составляющие матрицу R, должны занимать меньше места, чем параметры, задающий матрицу D, значит, поскольку размерности одинаковые, параметры должны дублироваться

2) Структура матрицы R должна позволять производить более быстрые вычисления

3) Качество на данных сети R не должно критично проседать по сравнению с D.

Авторы статьи нашли пример такой структуры, удовлетворяющую 3 вышеперечисленным требованиям. Это циркулярная структура.

Циркулярная структура существенно уменьшает объем необходимой памяти, чтобы хранить веса и позволяет использовать быстрое преобразование Фурье для перемножения матриц. Доля ошибок на CIFAR у сети R по сравнению с сетью D увеличивает всего на 0.3%.

Низкоранговая факторизация

Матрица преобразования в нейронной сети может быть многомерной, занимать большой объем памяти, умножение на такую многомерную матрицу - сложная операция. Один из выходов из ситуации - разложить такую матрицу в произведение матриц меньшей размерности, причем с возможностью варьирования промежуточных размерностей этих матриц. Для разложения многомерных тензоров используют polyadic decomposition (CP-декомпозиция, ее также часто называют CANDECOMP/PARAFAC моделью) .

Когда d=2, то CP-преобразование - это знакомое нам с детства SVD разложение. Ниже показана схема работы обычной свертки, 2d разложения и CP-преобразования.

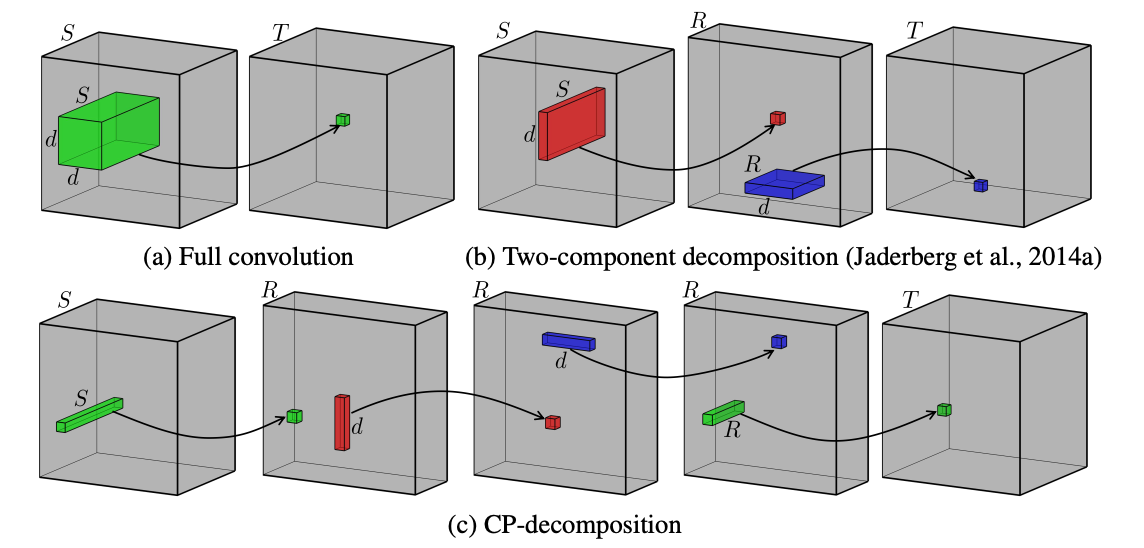
Без значительной просадки качества (в статье, где используют CP- разложение, можно добиться ухудшения качества на классификации ImageNet AlexNet-ом всего на процент), мы можем хранить (i_1+i_2+...i_d)*R параметров вместо i_1*i_2..*i_d, причем мы можем менять d в зависимости от наших приоритетов (память vs качество) + мы выигрываем по скорости при перемножении матриц.

Knowledge distillation

Основная идея этого класса методов - сначала обучить на каком-либо наборе данных большую сеть-учителя, затем, используя предсказания сети-учителя, обучить более легкую сеть-ученика, например, как это реализовано в статье. Плюсы такого подхода - когда мы учим сеть-ученика на предсказания сети-учителя, предсказания соответствуют определенной конкретной функции, которая существует в реальности, следовательно ее легче аппроксимировать, чем реальность с непонятными, сложными и не всегда гладкими законами. Плюс мы обладаем практически неограниченным набором данных для доучивания сети-ученика, поскольку нам больше не нужен таргет для примеров, а нужны только сами примеры - таргет мы получим самостоятельно, запустив применение сети-учителя.

Дополнением к такому подходу может случить hint, который авторы предлагают в статье, описывающей архитектуру FitNets. Суть заключается в следующем - кажется, ученику будет легче выучить выход учителя, если он будет представлять, что происходит внутри сети учителя. Давайте к обычной функции потерь добавим дополнительный лосс - расстояние от скрытого представления одного из центральных слоев учителя и одного из центральных слоев ученика, обработанного регрессором - функцией, которую мы также учим, сводящей представление скрытого слоя ученика к той же размерности, что была у скрытого слоя учителя.

где u_h и v_g - это функции скрытых слоев ученика и учителя, W_Hint и W_Guided - параметры этих слоев, а r - функция регрессора с параметрами W_r.

К недостаткам методов этого класса можно отнести то, что они работают только для задач с финальной функцией активации softmax. Также методы этого класса требуют большого количества допущений и на практике иногда показывают себя хуже, чем вышеперечисленные, более простые методы.

Вывод

Сжимать сети и ускорять их - очень актуальное и важное дело, в котором есть еще много простора для фантазии и улучшений.