Структуры данных - Binary search tree. Часть 4

Это Naize, всем здрасте!) Потихоньку движемся и завершаем циклы на разные тематики. Думаю, что самое время поговорить про структуры данных, там не так уж и много материала осталось. Собственно, это предпоследняя часть цикла Data Structurs, в которой мы узнаем, что такое binary search tree, AVL tree, red-black tree, B-tree и binary heap.

Материала будет много и он теоретический. Но, каждый кто так или иначе связан с IT должен про всё это знать, хотя бы поверхностно. Так что вперёд!

Двоичное дерево поиска

Двоичное дерево поиска (binary search tree) — это особый тип дерева, поиск в котором выполняется особенно эффективно. Узлы в двоичном дереве поиска могут иметь не более двух дочерних узлов.

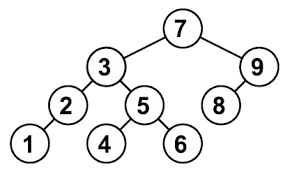
Кроме того, узлы располагаются согласно их значению/ключу. Дочерние узлы слева от родителя должны быть меньше него, а справа — больше (это хорошо видно на картинке). Чтобы вставить элемент, находим последний узел, следуя правилам построения дерева поиска, и подключаем к нему новый узел справа или слева.

Балансировка дерева

Если вставить в двоичное дерево поиска слишком много узлов, в итоге получится очень высокое дерево, где большинство узлов имеют всего один дочерний узел. Например, если последовательно вставлять узлы с ключами/значениями, которые всегда больше предыдущих, в итоге получится нечто, похожее на связный список.

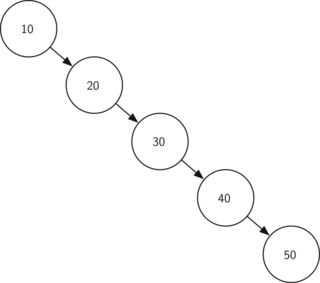
Однако мы можем перестроить узлы в дереве так, что его высота уменьшится. Эта процедура вызывается балансировкой дерева. Идеально сбалансированное дерево имеет минимальную высоту.

Большинство операций с деревом требует обхода узлов по ссылкам, пока не будет найден конкретный узел. Чем больше высота дерева, тем длиннее средний путь между узлами и тем чаще приходится обращаться к памяти. Поэтому важно уменьшать высоту деревьев.

Рассмотрим двоичное дерево поиска с n узлами и с максимально возможной высотой n. В этом случае оно похоже на связный список. Минимальная высота идеально сбалансированного дерева равняется log2(n) - опа, матан пошёл))) Сложность поиска элемента в дереве пропорциональна его высоте. В худшем случае, чтобы найти элемент, придется опускаться до самого нижнего уровня листьев.

Поиск в сбалансированном дереве с n элементами, следовательно, имеет O(logn). Вот почему эта структура данных часто выбирается для реализации множеств (где предполагается проверка присутствия элементов) и словарей (где нужно искать пары «ключ — значение»).

Однако балансировка дерева — дорогостоящая операция, поскольку требует сортировки всех узлов. Если делать балансировку после каждой вставки или удаления, операции станут значительно медленнее. Обычно деревья подвергаются этой процедуре после нескольких вставок и удалений.

Но балансировка от случая к случаю является разумной стратегией только в отношении редко изменяемых деревьев. Для эффективной обработки двоичных деревьев, которые изменяются часто, были придуманы сбалансированные двоичные деревья (self-balancing binary tree). Их процедуры вставки или удаления элементов гарантируют, что дерево остается сбалансированным.

Сейчас мы поговорим про некоторые self-balancing binary tree.

• Красно-черное дерево (red-black tree) — это хорошо известный пример сбалансированного дерева, которое "окрашивает" узлы красным либо черным цветом в зависимости от стратегии балансировки. Красно- черные деревья часто используются для реализации словарей: словарь может подвергаться интенсивной правке, но конкретные ключи в нем по-прежнему будут находиться быстро вследствие балансировки.

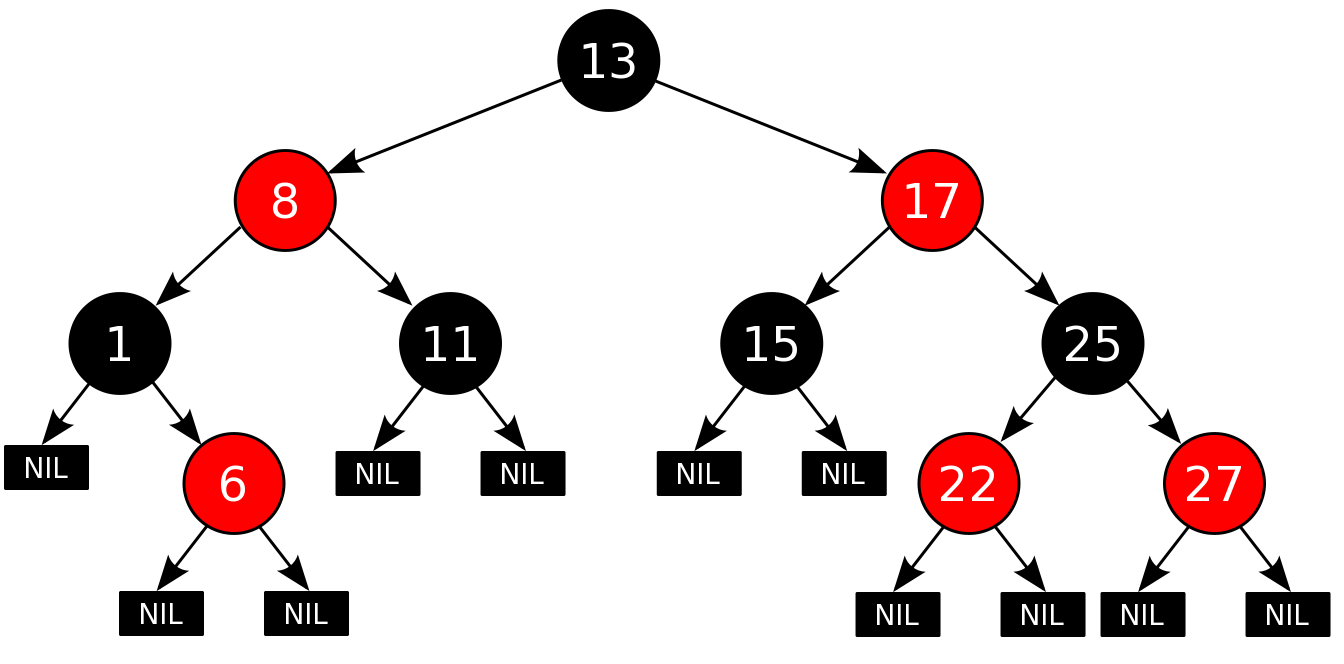
• AVL-дерево (AVL tree) — это еще один подвид сбалансированных деревьев. Оно требует немного большего времени для вставки и удаления элементов, чем красно-черное дерево, но, как правило, обладает лучшим балансом. Это означает, что оно позволяет получать элементы быстрее, чем красно-черное дерево. AVL-деревья часто используются для оптимизации производительности в сценариях, для которых характерна высокая интенсивность чтения.

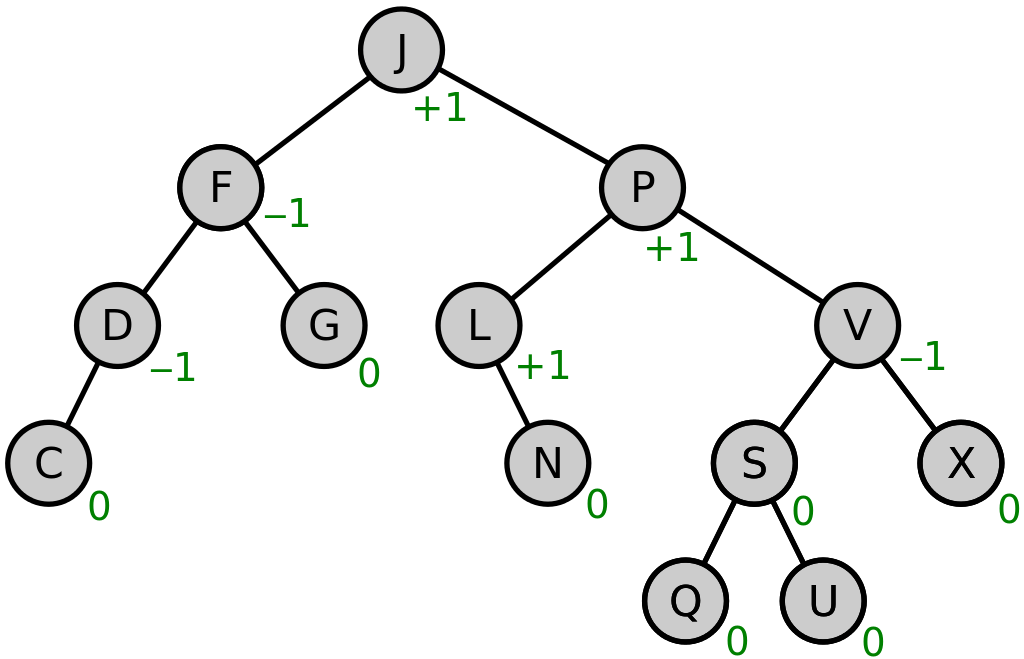
• Двоичное B-дерево (B-tree). В таких деревьях узлы могут хранить более одного элемента и иметь более двух дочерних узлов, что позволяет им эффективно оперировать данными в больших блоках. B-деревья обычно используются в системах управления базами данных.

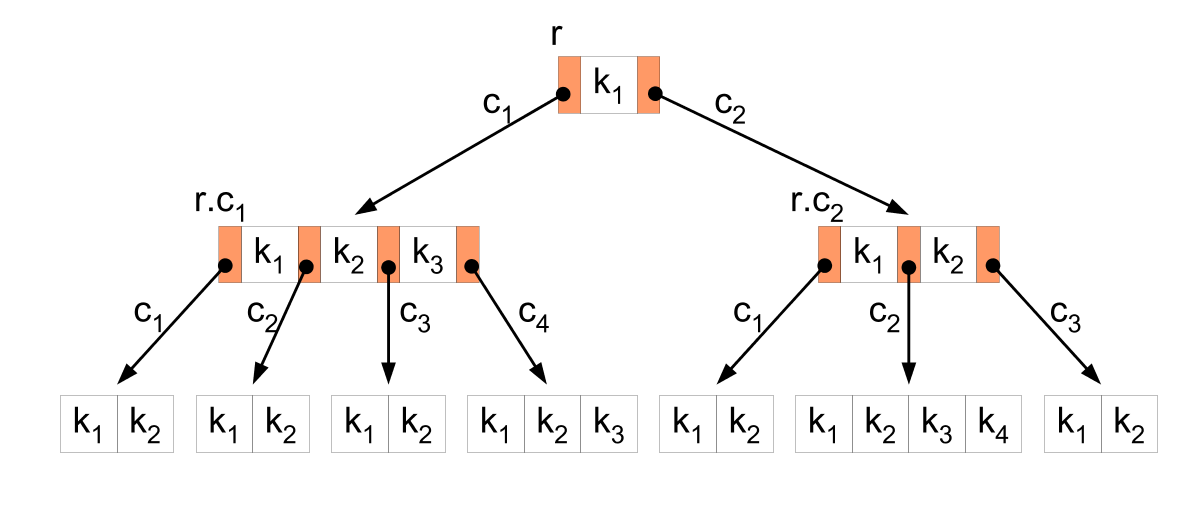
Двоичная куча

По английски binary heap — особый тип двоичного дерева поиска, в котором можно мгновенно найти самый маленький (или самый большой) элемент. Эта структура данных особенно полезна для реализации очередей с приоритетом. Операция получения минимального (или максимального) элемента имеет сложность O(1), потому что он всегда является корневым узлом дерева.

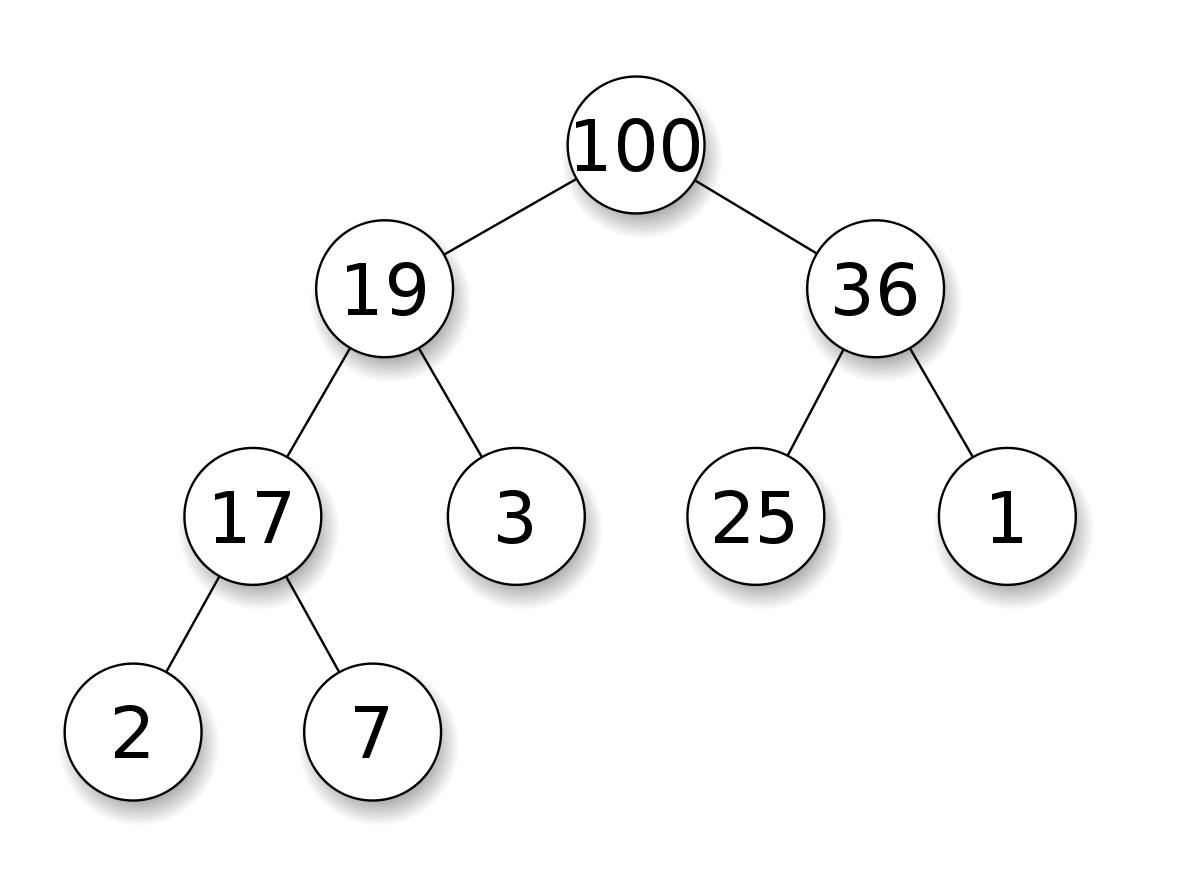
Поиск и вставка узлов здесь по-прежнему стоят O(logn). Кучи подчиняются тем же правилам размещения узлов, что и двоичные деревья поиска, но есть одно ограничение: родительский узел должен быть больше (либо меньше) обоих своих дочерних узлов.

Двоичная куча min-heap характерна тем, что значение в любой ее вершине не больше, чем значения ее потомков; в двоичной куче max-heap, наоборот, значение в любой вершине не меньше, чем значения ее потомков.

Обращайтесь к двоичной куче всегда, когда планируете часто иметь дело с максимальным (либо минимальным) элементом множества.

На сегодня всё, усваивайте полученные знания) Тема структур данных не самая простая и "с наскока" её трудно понять, поэтому важно понемногу разбираться. И если что-то не понятно, то стоит вернуться назад и посмотреть, не упустили ли вы какую-то важную деталь.

Хорошего вечера, и до субботы!)