Stereo Block Matching

Привет! Ранее я уже писал о методе префиксных сумм и его применении в компьютерном зрении. В этом посте расскажу о ещё одной, более сложной задаче компьютерного зрения из реальной жизни, в которой также можно использовать метод префиксных сумм.

Стереопара

Рассмотрим алгоритм, который по стереопаре находит расстояние от камеры до объектов. Стереопару можно получить с двух камер, направленных в одну точку, как глаза. Это два изображения с левой и правой камер. Их можно наложить друг на друга, и получится 3D-кино. Вот как выглядит стереопара:

Расстояния мы будем искать в виде карты глубины. Карта глубины - это изображение, на котором значения пикселей представляют расстояния от камеры до объекта, видимого в данном пикселе:

Давайте рассмотрим принцип, по которому по стереопаре можно получить карту глубины. Стереопару можно рассматривать как два глаза. Человеческие глаза тоже умеют определять расстояния до объектов. Посмотрим на картинку и попробуем представить, как видит человек.

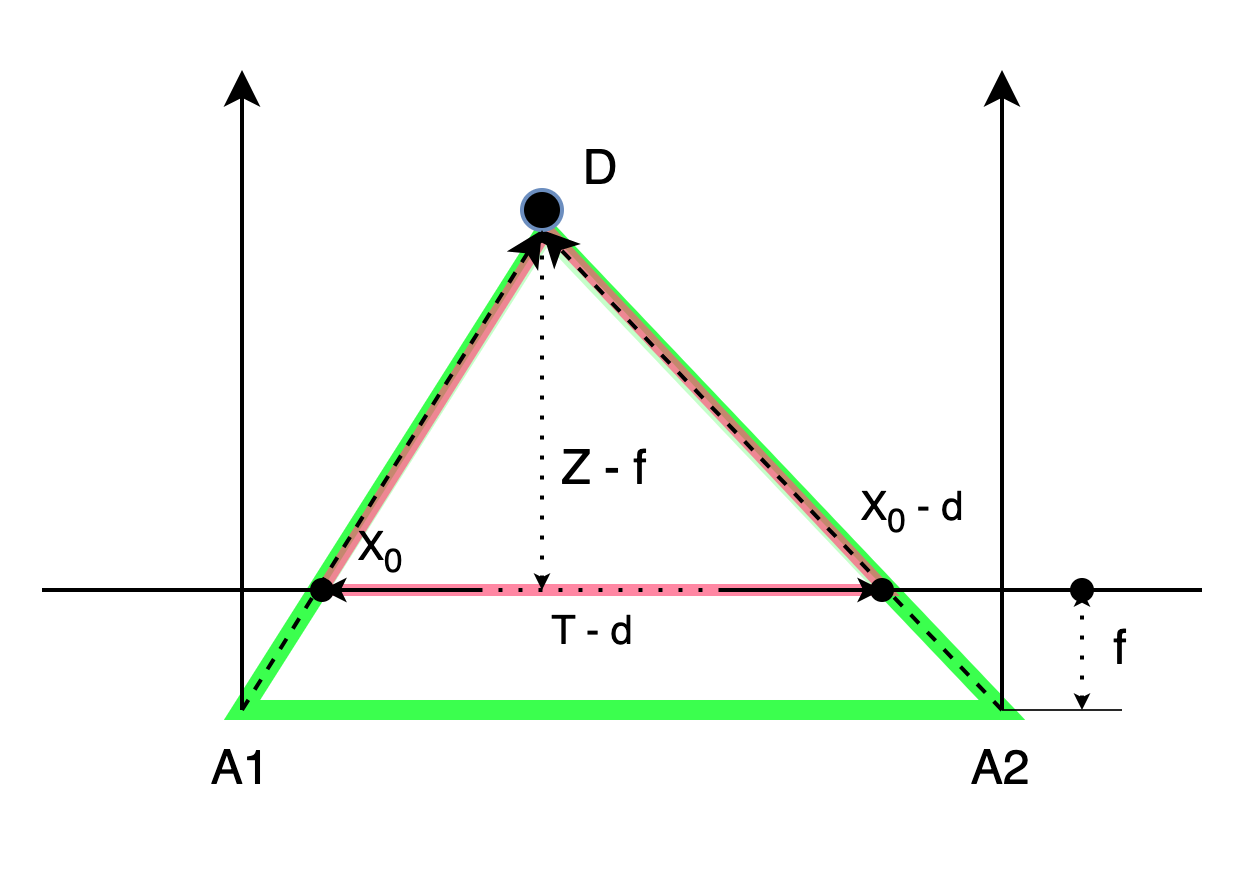
Здесь находится точка D - это точка, до которой мы хотим найти расстояние. Точка A1 - это левый глаз, A2 - правый. Для простоты представим, что у нас перед глазами находится стекло, на котором находится изображение. И точка X0 - пересечение стекла с прямой от левого глаза до точки, а точка X0 - d - пересечение стекла с прямой от правого глаза до точки. Здесь d - смещение объекта на правом изображении относительно левого.

Нам нужно найти расстояние Z. Применим формулу пропорции для треугольника:

Получим следующее уравнение:

Выражаем Z:

Проблема в том, что нам нужно как-то сопоставить то, что видит левый глаз, и то, что видит правый, чтобы понять, что они видят одну и ту же точку. То есть нужно найти точки X0 и X0 - d. Здесь мы будем предполагать, что такие точки находятся на одной и той же высоте. Фокусное расстояние и расстояние между камерами мы знаем. Поэтому задача состоит в том, чтобы для каждого пикселя на левом изображении найти d - насколько этот пиксель смещен на правом.

Подробнее о стереозрении можно прочитать в этой статье, из которой была взята эта секция :)

Stereo Block Matching

Для решения этой задачи существует несколько алгоритмов, и один из них - Stereo Block Matching.

Он основан на идее поиска похожих окрестностей конкретных пикселей. Мы будем рассматривать окрестности вокруг двух пикселей в виде квадратов.

Для каждого пикселя мы будем проходиться по всем возможным сдвигам, вычислять сумму разниц квадратов на левом и правом изображениях и выбирать квадрат с наименьшей суммой. Сдвиг этого наиболее похожего квадрата (d) будет отражать относительное расстояние до объекта.

В данном примере мы видим, что эти квадраты не сильно отличаются. Для оценки степени их схожести получим новый квадрат, в котором посчитаем поэлементную разницу. Чем меньше эта разница, тем лучше.

Получив квадрат, отражающий разницу между квадратами, мы можем посчитать сумму элементов в нем:

0 + 1 + 0 + 1 + 1 + 0 + 2 + 0 + 0 = 5

Для данного пикселя X0 на левом изображении переберем различные d, которые соответсвуют различным пикселям на правом изображении. Выберем d, соответсвующее минимальной сумме, и это будет расстоянием до объекта.

Стоит отметить, что кроме поэлементной разницы, существует и множество других функционалов. Но мы остановимся на этом.

Простое решение

В простом решении мы просто сделаем то, что описывает алгоритм в лоб. Пройдемся по каждому пикселю в левой картинке, перебирая смещения от 0 до определенного числа, например, до 1000. Для каждого пикселя на левой картинке будем проходить по всем пикселям в его окрестности и одновременно пройдемся по пикселям на правой картинке, учитывая смещение. Затем просуммируем их разницу. Это называется метрика SAD (Sum of Absolute Differences):

Помните, что мы умеем вычислять d, если умеем вычислять sad - для этого нужно взять d, для которого sad минимальное. При этом d является расстоянием до объекта.

Таким образом, формула расстояния до объекта выглядит так:

Приведем алгоритм для построения решения. Для простоты наши квадраты будут размера 3.

Псевдокод алгоритма

Код будет выглядеть так:

def stereo_block_matching(left_image, right_image):
    hight = len(left_image)
    width = len(left_image[0])
    # В результирующей картинке значения пикселей будут показывать расстояния до объекта (чем светлее, тем ближе)
    result = [[0 for x in range(width)] for y in range(hight)]
    for y in range(hight):
        for x in range(width):
            best_disparity = None
            best_difference = None
            for disparity in range(1000):
                difference = 0
                for shift_y in range(-1, 2):
                    for shift_x in range(-1, 2):
                        difference += abs(left_image[y][x] - right_image[y + shift_y][x + shift_x])
                if best_difference is None or difference < best_difference:
                    best_difference = difference
                    best_disparity = disparity
            result[y][x] = best_disparity
    return result

Давайте рассмотрим сложность этого алгоритма. Если предположить, что изображение квадратное размера N, мы исследуем смещения от 0 до d, и размер сравниваемого квадратного блока K, то итоговая сложность будет следующей:

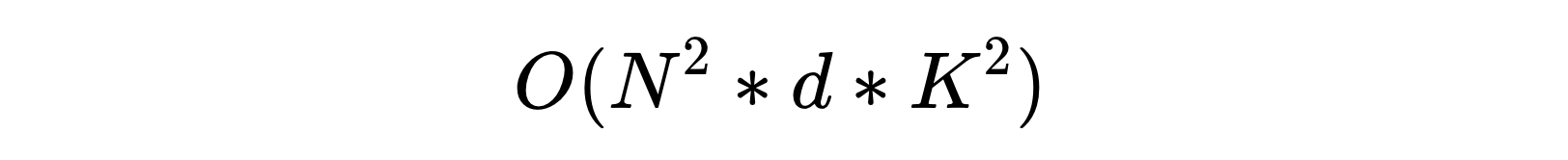
Решение методом частичных сумм

Если K равно 3, то в целом такая сложность не кажется критичной. Однако обычно K больше, так как чем больше окрестность, тем больше пикселей мы учитываем, и тем выше точность алгоритма. Но, конечно, если взять слишком большое K, алгоритм снова будет менее точным. Например, размер 21 часто используется. В этом случае K * K больше четырехсот. Если бы мы могли избавиться от K * K в асимптотике, можно было бы здорово сэкономить.

В этом нам может помочь метод частичных сумм. Идея заключается в переиспользовании подсчитанной суммы. Сейчас мы вычисляем сумму разностей в окрестности пикселей, затем переходим к ее подсчету для следующего смещения, и пересчитываем заново, только добавляя новый столбец и удаляя старый. Мы можем не пересчитывать всю сумму заново, а пересчитывать только новый и старый столбцы. Идея аналогична той, что используется для box filter. То же самое происходит при переходе на следующую строку. Мы теряем часть уже посчитанных сумм, нужно лишь добавить новую строку и удалить старую, а мы пересчитываем все. Однако можно пересчитать только новую и старую строки.

Column_sad

Теперь более подробное описание. Введем переменную column_sad - это суммарная разница пикселей для части столбца.

Давайте рассмотрим пример значения column_sad[x, y]:

В этом примере column_sad[x, y] будет равен 1 + 1 + 0 = 2.

Формула для подсчета column_sad выглядит так:

Быстрый подсчет column_sad

Эту переменную можно легко пересчитать за константное время, используя её значение с предыдущей строки.

Давайте рассмотрим пример быстрого пересчета:

В этом примере column_sad[x, y] будет равен (1 + 1 + 0) + 8 - 1 = 9.

Подсчет SAD с помощью column_sad

С использованием column_sad для столбца можно легко вычислить SAD для всего квадрата:

Более того, эту сумму тоже можно вывести, используя предыдущее значения:

Вот пример быстрого пересчета SAD:

Таким образом, sad[x, y] = ((0 + 1 + 2) + (1 + 1 + 0) + (0 + 0 + 0)) + (3 + 2 + 4) - (0 + 1 + 2) = (1 + 1 + 0) + (0 + 0 + 0) + (3 + 2 + 4) = 2 + 0 + 9 = 11

Пересчитывая для каждого значения y сначала значения column_sad, а затем, зная эти значения, вычисляя sad для данного пикселя и данного смещения, получаем асимптотику:

Также можно заметить, что значения sad и column_sad для различных смещений не зависят друг от друга, поэтому их можно считать отдельно, и, соответственно, хранить лишь w памяти для column_sad.

Код алгоритма

from PIL import image

def stereo_block_matching(left_image, right_image):
    hight = len(left_image)
    width = len(left_image[0])
    # В результирующей картинке значения пикселей будут показывать расстояния до объекта (чем светлее, тем ближе)
    result = [[0 for x in range(width)] for y in range(hight)]

    column_sad = [[[]]]
    sad = [[[]]]
    block_size = 21
    s = block_size // 2

    for y in range(hight):
        for x in range(width):
            best_disparity = None
            best_difference = None
            for d in range(100):
                sad[y][x][d] = column_sad[y][x + s][d] \
                               + sad[y][x - 1][d] \
                               + column_sad[y][x - s - 1][d]
                column_sad[y][x][d] = abs(left_image[y + s][x] - right_image[y + s][d]) \
                                      + column_sad[y - 1][x][d] \
                                      - abs(left_image[y + s][x] - right_image[y + s][d])
                if best_difference is None or sad[y][x][d] < best_difference:
                    best_difference = sad[y][x][d]
                    best_disparity = d
            result[y][x] = best_disparity
    return result

Заключение

На этом всё. Мы рассмотрели применение метода префиксных сумм в довольно необычной роли - для определения расстояния от камеры до объекта.

В одном из следующих постов я расскажу о том, как реализовать этот алгоритм еще более эффективно на процессоре, который поддерживает SIMD, с интересным лайфхаком.

В телеграм-канале @polyprogrammist_dev вы можете посмотреть больше постов и обсудить этот пост.