Создание собственной симуляции активной материи на Python

Сегодня наша задача — создать симуляцию активной материи, т. е. роевое поведение. С помощью этой системы можно имитировать поведение стаи птиц или косяка рыб, а также увидеть, как из простых правил появляются самоупорядоченные движения.

Сопровождающий код Python на github.

Для начала посмотрите, как выглядит симуляция при запуске:

Модель Вичека для поведения стаи

Разберём известную минимальную модель активной материи — модель Вичека (1995 г.). Несмотря на простоту модели, она отображает общие свойства роевого поведения.

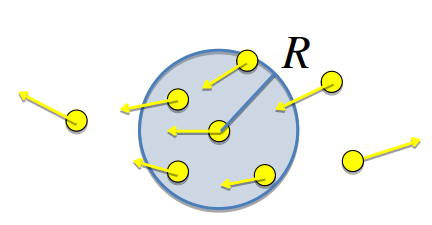
Модель состоит из N движущихся частиц, индексируемых на i=1,…, N. У каждой частицы есть угол направления Θᵢ, по которому она движется. Все они двигаются с одинаковой скоростью v₀. Частицы взаимодействуют друг с другом внутри радиуса взаимодействия R, в результате чего изменяют своё направление (угол).

На каждой фазе положении rᵢ каждой частицы i обновляется следующем образом:

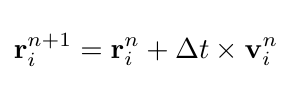
В соответствии со скоростью частицы vᵢ:

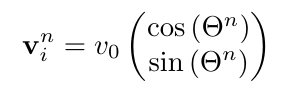
Динамичность модели Вичека зависит от того, как сменяются углы. А их смена происходит согласно следующему правилу:

Где первый член  —  этосредний угол направлениявсех соседей частицы i внутри R (включая саму частицу). А второй ηᵢ — это случайное отклонение, полученное в результате равномерного распределения [-η/2,η/2].

Код симуляции

Эта модель настолько проста, что весь Python код можно изложить в одном блоке, как приведено ниже. Для вычисления среднего угла мы сложили все соседние векторы и использовали функцию numpy: arctan2, чтобы вернуть значение угла в правильном квадранте. Также мы взяли L как размер периодической области.

# Параметры симуляции
v0   = 1.0  # Скорость
eta  = 0.5  # случайный угол отклонения (в радианах)
L    = 10   # размер области
R    = 1    # радиус взаимодействия
dt   = 0.2  # фаза
Nt   = 200  # количество фаз
N    = 500  # количество частиц

# положения частицы 
x = np.random.rand(N,1)*L
y = np.random.rand(N,1)*L

# скорость частицы
theta = 2 * np.pi * np.random.rand(N,1)
vx = v0 * np.cos(theta)
vy = v0 * np.sin(theta)

# Симуляция Main Loop
for i in range(Nt):

    # движение
    x += vx*dt
    y += vy*dt
    
    # применение периодических пограничных условий
    x = x % L
    y = y % L
    
    # найти средний угол соседей в диапазоне R
    mean_theta = theta
    for b in range(N):
        neighbors = (x-x[b])**2+(y-y[b])**2 < R**2
        sx = np.sum(np.cos(theta[neighbors]))
        sy = np.sum(np.sin(theta[neighbors]))
        mean_theta[b] = np.arctan2(sy, sx)
        
    # добавление случайного отклонения
    theta = mean_theta + eta*(np.random.rand(N,1)-0.5)
    
    # изменение скорости
    vx = v0 * np.cos(theta)
    vy = v0 * np.sin(theta)

Меняя параметры симуляции, можно создавать разные паттерны поведения стаи. Кроме того, симуляция может отобразить фазовый переход между изотропным движением и обычным поведением. В примере выше имитация происходит согласно текущим параметрам модели.

При запуске кода можно посмотреть на симуляцию в реальном времени, благодаря фигурам, изображающим положение частиц после 200 фаз:

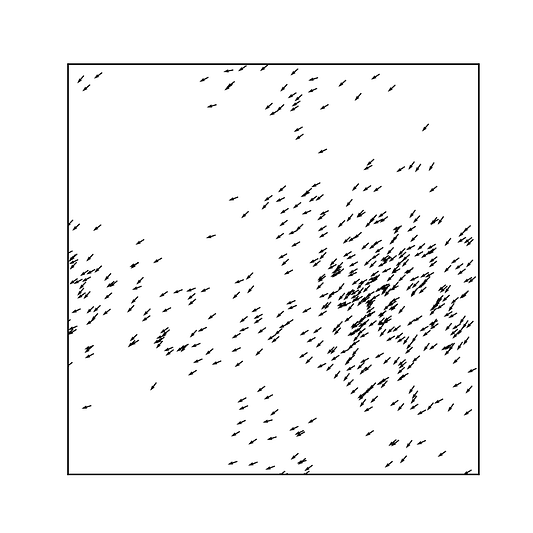
Модель Вичека очень проста и полезна. Она описывает коллективное движение, при котором отдельные частицы расходуют энергию, в результате чего теряют термическое равновесие.

В природе скворцы ведут себя подобным же образом. Их танец возникает из-за того, что одна птица пытается, как можно, точнее имитировать движение соседней. 

Существует множество дополнений к модели Вичека и к другим моделям активной материи. Но об этом не в этой статье. 

Другой пример активной материи — это скопление бактерий на микроскопическом уровне:

Скачайте код с github и посмотрите на поведение стаи в соответствии с моделью Вичека, а также меняйте параметры и изучайте изменения в движении.

https://t.me/pythonl

источник