Решение. Цветочный город (#117)

Конструктивное доказательство

Рассмотрим граф города Цветочный, в котором вершины (В) – площади, и рёбра (Р) – улицы. Для одной из компонент связности графа должно выполняться неравенство

Р ≥ В + 1   (*)

так как в противном случае соответствующее неравенство будет нарушено для всего графа.

Из уравнения Эйлера для связного планарного графа

В – Р + Г = 1   (здесь мы намеренно не учитываем внешнюю грань, поэтому справа стоит 1)

и неравенства (*) следует неравенство

Г ≥ 2

Поэтому в графе найдётся как минимум два разных цикла. Возможно, эти циклы имеют общие вершины и рёбра, но как минимум одно ребро у них разное.

Инвариант цикла (при переименовании) – чётность количества улиц каждого цвета. Действительно при любом переименовании количество, например, красных улиц в цикле, либо

-       не меняется, если вершина не входит в цикл или из вершины в цикл выходили улицы разных цветов

-       увеличивается на 2, если из вершины в цикл выходили две синие улицы

-       уменьшается на 2, если из вершины в цикл выходили две красные улицы

Рассмотрим два случая.

1. Есть цикл с чётным количеством вершин (а, значит, и рёбер). Пусть одна улица будет красной, остальные – синие. В силу инварианта в цикле количество красных улиц никогда не станет чётным, следовательно, в цикле обязательно будут улицы разных цветов.

2. Если цикла с чётным количество вершин нет, то в силу рассуждений выше обязательно будут два цикла с нечётным числом вершин. В этих циклах нужно просто задать разную чётность у определённого цвета. Например, в одном цикле пусть все улицы будут синие, а в другом – все, кроме одной. Тогда в силу инварианта чётность синих улиц всегда будет разная в двух циклах. Но ведь циклы имеют одинаковую чётность улиц, следовательно, в циклах обязательно будут улицы разных цветов.

Заметим, что циклы могут странным образом пересекаться, но для каждого из них верен свой независимый инвариант. Как в следующем примере из 5 площадей и 6 улиц:

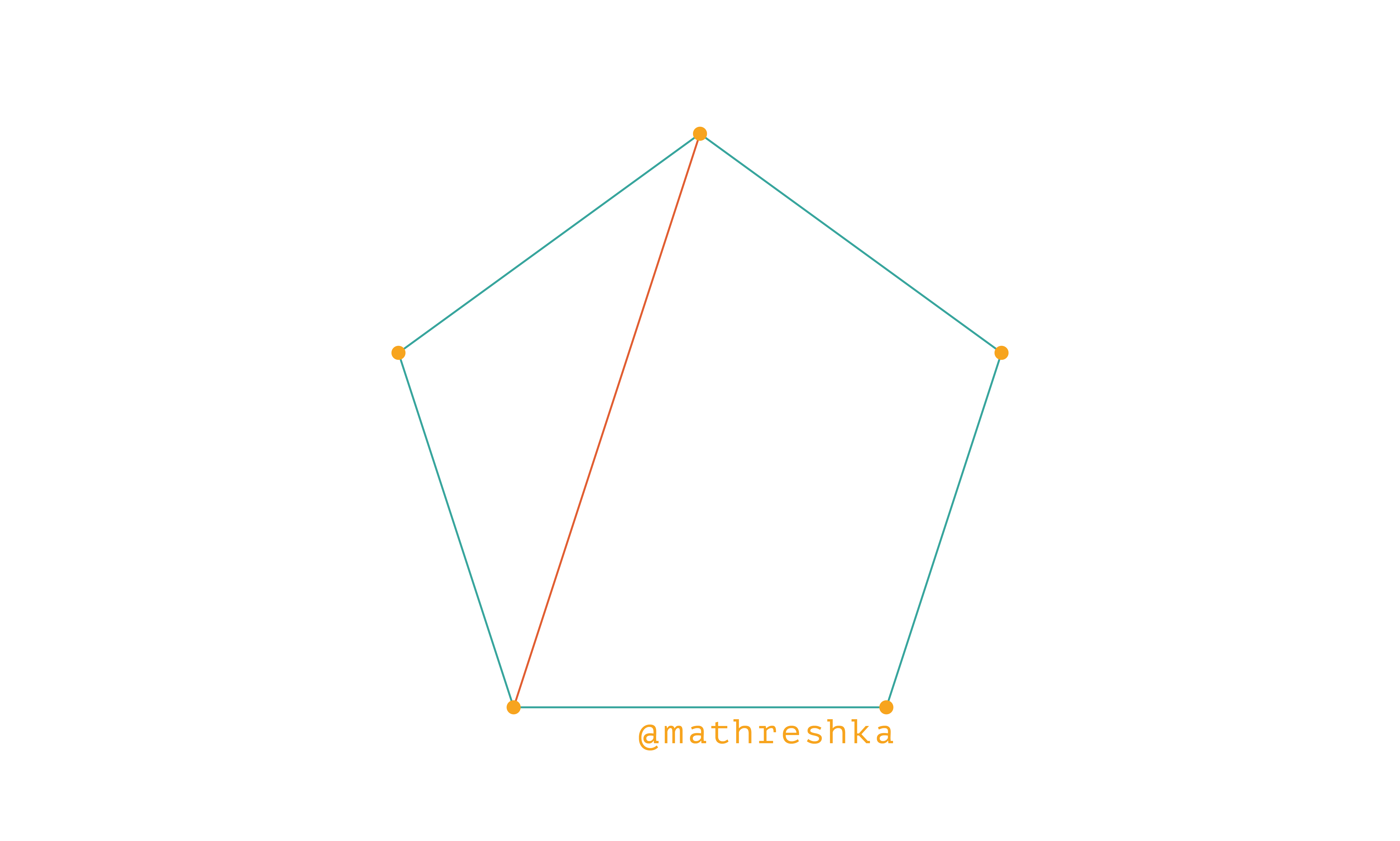
Следовательно, в любом случае переименованиями нельзя добиться одинаковых названий у всех рёбер-улиц.

Неконструктивное доказательство

Альтернативное решение без предъявления искомой раскраски можно посмотреть здесь.

Условие  
Telegram