Решение. Задача Бернулли-Эйлера о перепутанных письмах (#141)

Ответ: 265

Решение рекуррентное

Рассмотрим квадрат n×n, на диагонали которого закрашено k клеток. Обозначим D(n, k) количество расстановок n ладей, при которых они не бьют друг друга и не стоят на закрашенных клетках. 

Докажем, что при k≥1

(*) D(n, k-1) = D(n-1, k-1) + D(n, k)

Для этого рассмотрим квадрат n×n, на диагонали которого закрашено k-1 клеток. Выделим столбец, в котором диагональная клетка не закрашена. Тогда D(n, k-1) складывается из количества расстановок, при которых ладья в выделенном столбце является диагональной и не является. В первом случае это количество равно D(n-1, k-1), во втором – D(n, k). 

Во вступительном слове было отмечено, что D(n,n) совпадает с тем самым количеством способов перепутать n писем, которое нас интересует. Положим D(0, 0) = 1. Ясно, что D(n, 0) = n!, поэтому с помощью равенства (*) уже возможно найти D(6, 6):

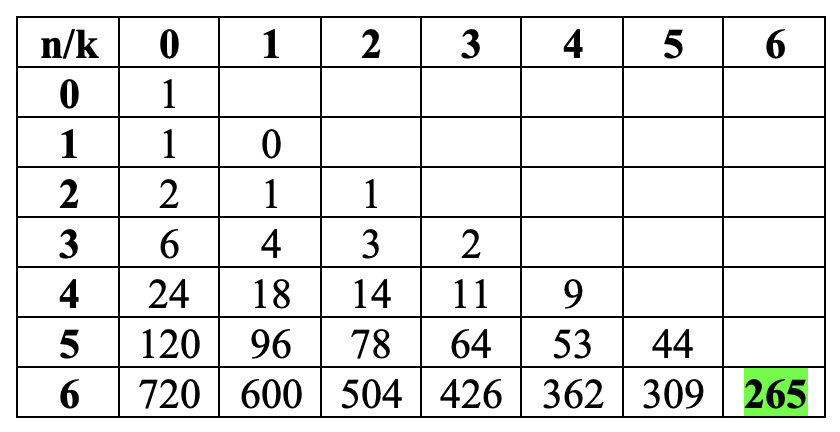
Выведем более удобную формулу для подсчёта D(n,n):

D(n+1, n+1) = n(D(n-1, n-1) + D(n, n))

Для этого рассмотрим квадрат (n+1)×(n+1), на диагонали которого закрашено n+1 клеток, и выделим произвольный столбец. Тогда при фиксированной позиции ладьи в выделенном столбце количество расстановок оставшихся ладей равно D(n, n-1). Количество способов выбрать ладью в выделенном столбце равно n, поэтому D(n+1, n+1) = nD(n, n-1). Применяя равенство (*) при k=n, получаем требуемое. 

Теперь подсчёт D(6, 6) становится гораздо быстрее:

D(1, 1) = 0, D(2, 2) = 1, D(3, 3) = 2, D(4, 4) = 9, D(5, 5) = 44, D(6, 6) = 265

Решение по формуле включений-исключений

Для того, чтобы применить указанную формулу требуется установить объекты и их свойства:

объект i = письмо с номером i
свойство i = письмо с номером i попало в свой конверт

Обозначим N(i_1, …, i_k) – количество объектов, обладающих свойствами i_1, …, i_k. Другими словами, это количество способов раскладки писем, при которых хотя бы письма с номерами i_1, …, i_k попадут по адресу (но не обязательно только они). А это количество уже легко подсчитать, и равно оно (n-k)!

По условию задачи нужно найти количество объектов F(n), не обладающих ни одним свойством. Тогда прямое применение формулы включений-исключений приводит к выражению

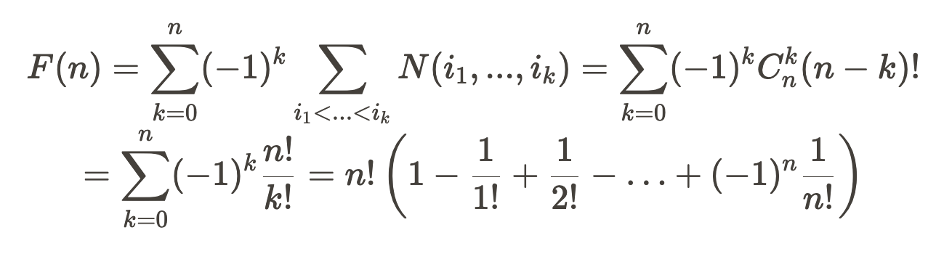
Легко убедиться прямой подстановкой, что указанная формула приводит ровно к тому же ответу, что и решение с использованием рекуррентных соотношений.

Условие
Telegram