Симметрия в ранговой теории (часть 3)

11. Отсутствие H-регуляции и альтернативных маршрутов в современных LLM

11.1 Альтернативные маршруты как свойство ранговой динамики

В ранговой теории под альтернативным маршрутом понимается не просто другой последовательный вывод, а переключение между конкурирующими цепями Маркова, возникающее в результате контекстного регулирования симметрии внутри вырожденных групп.

Пусть входной сигнал системы задан распределением X=(x1,x2,… ) и модель формирует предсказание Y=(y1,y2,… ) В классической интерпретации Predictive Coding вводится ошибка E=X−Y которая трактуется как шум или отклонение.

Однако в рамках ранговой теории величина, аналогичная E, не является ошибкой, а отражает остаточную симметрию и недоподавленные элементы внутри вырожденных групп.

Если входной сигнал X имеет распределение вероятностей по токенам и модель предсказывает Y, то отклонение E=X−Y отражает несовпадение между ожиданием и предсказанием. Сильные компоненты E могут указывать на элементы входа, которые модель не смогла "подавить" или интегрировать в предсказание, что интерпретируется как сигнал новизны или аномалии.

Пример: X=(0.02,0.01), Y=(0.015,0.001)
Тогда E=X−Y=(0.005,0.009)

Видим, что вторая компонента 0.009 значительно превышает первую. Это значит, что модель не уверена в подавлении второго сигнала, и он потенциально может инициировать альтернативный маршрут предсказания.

На следующем шаге, происходит контекстное усиление и формирование альтернативного маршрута X′=X * E. Это не корректировка ошибки, а перераспределение вероятностей в ранговом пространстве, согласованное с предыдущей структурной неопределённостью.

Мы получаем перераспределение важности токенов:

X′=X * E=(0.04,0.03)∗(0.005,0.009)=(0.0002,0.00027)

Теперь второй элемент усилен относительно первого, что может привести к выбору альтернативной последовательности предсказаний.

Именно так в ранговой теории возникает альтернативный маршрут, рассуждения появляется как следствие работы с симметрией, а не как результат внешнего шума.

В современных больших языковых моделях (LLM) на базе трансформеров отсутствует явный механизм для построения альтернативных маршрутов предсказания токенов. Под альтернативным маршрутом мы понимаем последовательность предсказаний, которая отличается от основной траектории, но может быть потенциально оптимальной в контексте текущего входного распределения.

11.2 Почему современные LLM не обладают этим механизмом

Современные трансформеры пытаются моделировать альтернативные маршруты через Chain-of-Thought (CoT). Однако, в этом случае LLM не оценивает реальный эффект отклонений E на вход: она искусственно обучается генерировать распределения, которые "симулируют" влияние E.

Главное отличие:

• В классическом CoT модель всегда формирует альтернативные распределения, вне зависимости от того, действительно ли сигнал E должен изменить предсказание.
• Настоящее формирование альтернативного маршрута требует, чтобы распределение E фактически воздействовало на будущие шаги, усиливая или подавляя определённые токены в соответствии с их "новизной" или H-энтропией.

В трансформерных LLM отсутствует явный механизм H-регуляции:

• нет отдельного канала контекстной энтропии;
• нет динамического перераспределения симметрии внутри вырожденных групп;
• нет конкуренции цепей Маркова на уровне распределений.

Вместо этого используется имитация альтернативных маршрутов через Chain-of-Thought (CoT).

11.3 Ключевое различие

В контексте ранговой теории и теорем о вырождении, можно интерпретировать E не как показатель новизны, а как H-энтропию, работающую с симметрией в распределении.

Эффект E аналогичен направлению в подпространстве вырождения: сильные компоненты создают "альтернативные маршруты" предсказания, которые модель может следовать при стохастическом или детерминированном разрешении вырождения. Таким образом, H-энтропия становится ключевым инструментом для работы с симметрией и естественного формирования альтернативных маршрутов, в отличие от искусственного CoT.

В ранговой теории альтернативный маршрут возникает условно, только если симметрия действительно требует регулирования. В LLM с CoT альтернативный маршрут навязывается всегда, независимо от структуры входного распределения. Иначе говоря, модель обучается выдавать результат так, как если бы существовал значимый E, даже если фактически симметрия отсутствует. Это приводит к избыточным рассуждениям, ложным альтернативам и деградации устойчивости при росте длины вывода.

11.4 Ошибка, новизна и неверная интерпретация E

В работе Google “It’s All Connected: A Journey Through Test-Time Memorization, Attentional Bias, Retention, and Online Optimization” (архитектура Titans, фреймворк MIRAS) величина E=X−Y интерпретируется как сигнал новизны, используемый для записи информации в кратковременную память.

Здесь E трактуется как показатель новизны:

• Если E содержит аномалию, модель считает, что столкнулась с новым сигналом.
• В рамках MIRAS, это используется для фильтрации и запоминания данных в кратковременной памяти.

Однако в рамках ранговой теории, E не является новизной, а представляет собой направление вырождения и H-энтропию, которая определяет чувствительные альтернативные маршруты в распределении токенов. Это подтверждает, что настоящие альтернативные маршруты формируются не искусственно, а через естественные свойства распределения и симметрию, как описано в теоремах S.1–S.4. Аналогично, медленная релаксация и высокая дисперсия в подпространстве вырождения (Теорема S.4) объясняет, почему модель может выбрать альтернативный маршрут только при наличии значительного сигнала в H-энтропии.

Следовательно:

E — это не индикатор новизны.
E — это проявление H-энтропии, связанной с симметрией рангового пространства.

Использование E как фильтра памяти приводит к накоплению неструктурированных состояний, а не к выявлению действительно новых структурных уровней.

Современные LLM:

• не обладают механизмом H-регуляции;
• не формируют альтернативные маршруты как следствие симметрии;
• имитируют конкуренцию гипотез через обученные шаблоны.

В отличие от этого, в ранговой теории:

• альтернативные маршруты возникают естественно;
• они являются следствием работы с вырожденными группами;
• их появление строго обусловлено структурой распределений.

Это различие является фундаментальным и объясняет, почему LLM не способны к подлинному контекстному сомнению, устойчивому переключению гипотез и структурно обоснованному критическому мышлению.

Современные LLM без явного H-механизма не имеют встроенного способа формировать альтернативные маршруты предсказаний.

Отклонение E=X−Y можно использовать для оценки направлений в подпространстве вырождения, где система чувствительна к симметрии.

H-энтропия обеспечивает естественный механизм альтернативных маршрутов, в отличие от CoT, который симулирует этот эффект искусственно.

Теоремы S.1–S.4 дают строгую математическую основу для анализа чувствительности, дисперсии и времени релаксации в направлениях вырождения, что напрямую связано с формированием альтернативных маршрутов.

12. Вырожденные группы, вложенные ранговые пространства и формирование Марковских одеял

12.1 Вырожденные группы как носители латентной структуры

В рамках ранговой теории устойчивые ранги соответствуют устойчивым асимметриям распределения и, следовательно, обладают уникальной структурной интерпретацией. Такие ранги не допускают дальнейшего внутреннего структурирования, поскольку:

1. они асимметричны;
2. они статистически различимы;
3. их элементы не образуют симметричных классов эквивалентности.

Напротив, вырожденные группы определяются как подмножества элементов рангового пространства, для которых маргинальные вероятности неразличимы в рамках текущего разрешения модели. Эти группы обладают следующими свойствами:

• элементы внутри группы симметричны относительно функционала ранговой стоимости;
• группа может накапливать произвольно большое число элементов;
• информация, содержащаяся в группе, является латентной и не может быть использована напрямую в текущем ранговом пространстве.

Тем самым, вырожденные группы выступают единственным кандидатом на роль носителя потенциальной структуры более высокого уровня. Устойчивые ранги, будучи уже разрешёнными асимметриями, не обладают этим свойством и потому не могут служить основой для формирования вложенного рангового пространства.

12.2 Регуляризация и возникновение нового сигнального уровня

Ключевым элементом ранговой теории является различие между:

• входным сигналом как эмпирическим распределением,
• выходным сигналом как оптимальным распределением,
• H-регуляризацией как контекстным функционалом, не порождающим динамику, но изменяющим устойчивость альтернатив.

В этом смысле корректно утверждение:

причиной возникновения нового сигнального уровня является не вход сам по себе, а композиция (входное распределение * регуляризация).

Именно эта композиция формирует обобщённый сигнал, который может содержать структуру, отсутствующую в исходном входе.

Важно подчеркнуть: ранговая теория не восстанавливает причинность входа, а работает исключительно с устойчивыми асимметриями распределений. Исходно ранговое пространство симметрично и не содержит информации о структуре. Структура возникает только в результате нарушения симметрии под действием регуляризации.

Следовательно, симметричные (вырожденные) группы являются единственным источником новых ранговых пространств, поскольку только они имеют потенциал к накоплению новой информации.

12.3 Гипотеза о формировании вложенных Марковских одеял

На основании вышесказанного формулируется следующая вложенного рангового пространства. При достаточном накоплении элементов в вырожденной группе и наличии устойчивого регуляризующего контекста система может сформировать внутри этой группы новое ранговое пространство, соответствующее вложенному Марковскому одеялу.

Важно отметить, что:

• ранговая теория описывает механизм выделения структуры;
• Марковское одеяло описывает разделение ролей и границ взаимодействия;

Хотя прямого тождества между ними нет, мы может сказать, что ранговая теория описывает внутренний процесс, который может индуцировать формирование Марковского одеяла, но не заменяет его теорию.

12.4 Нейробиологическая интерпретация

Рассмотрим область мозга, устойчиво выделяющую определённый тип асимметрий, например акустические сигналы.

В рамках ранговой теории:

1. формируются устойчивые ранги, соответствующие базовым признакам звука;
2. в хвосте распределения накапливаются вырожденные группы, соответствующие неразличимым или слабоструктурированным комбинациям;
3. эти группы растут по мере накопления статистики.

Гипотеза состоит в том, что при определённых условиях вырожденная группа может перейти в новое ранговое пространство, обрабатывающее сигнал иного типа (например, структуру в звуке — речь).

Это связано с тем, что у нас возникает сигнал нового уровня. Пусть R это текущая ранговая область с входным сигналом X. Она состоит из рангового пространства (маргинальные вероятности) и иерархического марковского пространства (условные вероятности → цепи Маркова). Ранговое пространство состоит из рангов: уникальных элементов с устойчивыми асимметриями и вырожденных групп (симметричных множеств → статистически равновероятных элементов). Каждый уровень иерархии формирует ранговое пространство, кодирующее выходной сигнал для следующего уровня. Поэтому мы получаем: ранговое пространство → марковское пространство → ранговое пространство.. . Каждый уровень иерархии марковского пространства предсказывает сигнал "Y" и "H = X - Y", где H это регуляризация контекста. Вырожденные группы имеют неопределённость внутри себя из-за симметричного распределения вероятности внутри группы. H разрушает эту симметрию, за счет создания сигнала нового типа → X*H (X внутри вырожденный группы одинаковый для всех элементов группы/ранга). Поэтому система вынуждена минимизировать затраты, стремясь предсказать сигнал внутри группы (найти закономерности), пытаясь выделить в нем асимметрию. Мы получаем вложенную ранговую область, внутри R, со своим ранговым и марковским пространством, и своей иерархией. С точки зрения биологии, это порождает новую область мозга из вырожденной группы, которая обрабатывает новый тип сигнала.

Ранее, схожая модель была рассмотрена на примере конечных автоматов. Данная модель, очень схожа с Марковским одеялом, которое будет рассмотрено ниже.

12.5 Ансамбли, изоляция и роль Марковского одеяла

Одна из возможных интерпретаций, заключается в том, что:

1. Вырожденная группа реализуется как растущий ансамбль элементов (например, нейронов).
2. По мере роста ансамбль становится статистически и функционально отличимым.
3. Для сохранения симметрии внутри группы требуется частичная изоляция от внешнего рангового пространства.

Такая изоляция индуцирует структуру, аналогичную Марковскому одеялу:

• часть элементов берёт на себя роль взаимодействия с внешним сигналом (ранговое пространство);
• часть — роль внутренней переработки (марковское пространство);
• часть — роль обратного воздействия (ранговое пространство в последнем уровне иерархии, ведущее на выход).

Важно, что изоляция здесь не абсолютна, а функциональна — ансамбль взаимодействует с внешним миром только через собственное ранговое представление.

12.6 Иерархия вероятностей и неизбежность трёх ролей

Но мы знаем, что из структуры ранговой теории следует важное наблюдение:

1. Ранговое пространство: на нижнем уровне формируются маргинальные вероятности — вход.
2. Марковское пространство: на промежуточных уровнях возникают условные вероятности, не связанные напрямую с входом, а работающие в пространстве рангов.
3. Ранговое пространство: каждый уровень иерархии порождает собственное оптимальное распределение для кодирования сигнала на верхнем уровне. Поэтому финальный уровень иерархии порождает распределение, которое кодирует выходной сигнал.

Это приводит к неизбежному разделению ролей:

• вход (маргинальные вероятности),
• внутренняя иерархия (условные вероятности),
• выход (оптимальное распределение).

Эти роли: функционально различны, частично изолированы, связаны только через ранговые представления.

Таким образом, хотя ранговая теория не описывает физический механизм образования Марковского одеяла, она естественным образом предсказывает необходимость ролевого разделения, совместимого с его формальной структурой.

1. Вырожденные группы — единственный источник вложенных структур.
2. Новые ранговые пространства возникают как результат нарушения симметрии под действием регуляризации.
3. Формирование Марковского одеяла не тождественно ранговой теории, но может быть индуцировано ею.
4. Ролевая структура (сенсорное / внутреннее / латентное / активное) возникает как следствие иерархии вероятностей, а не как исходное предположение.
5. Механизм пространственно-физического разделения ролей остаётся открытым и требует расширения теории.

13. Эксперимент Lenski LTEE как эмпирический пример эндогенного формирования рангового пространства

13.1 Краткое описание эксперимента

Long-Term Evolution Experiment (LTEE) (ссылка на эксперимент), начатый Ричардом Ленски в 1988 году, представляет собой контролируемое эволюционное исследование, в котором 12 изолированных популяций E. coli выращиваются в строго фиксированной среде на протяжении десятков тысяч поколений.

Ключевые свойства эксперимента:

• среда строго изолирована;
• состав питательного раствора неизменен;
• эксперимент повторяем и реплицируем;
• отсутствует внешний ввод нового сигнала или нового ресурса во времени.

Среда содержит глюкозу как основной источник энергии и цитрат (Cit) как побочный компонент, который E. coli в аэробных условиях изначально усваивать не может.

13.2 Феномен Cit⁺ как качественный фазовый переход

Примерно через ~31 000 поколений в одной из линий возникает способность усваивать цитрат в присутствии кислорода (фенотип Cit⁺). Это событие обладает рядом принципиально важных характеристик:

1. Отсутствие внешнего изменения среды
2. Cit присутствовал в среде с самого начала эксперимента.
3. Редкость и уникальность события
4. Cit⁺ возник только в одной из 12 независимых линий.
5. Наличие длительного плато до перехода
6. До появления Cit⁺ наблюдалось длительное насыщение адаптивных улучшений.
7. Комбинационный характер мутации
8. Переход стал возможен только после накопления ряда «подготовительных» мутаций, которые сами по себе не давали фенотип Cit⁺.

Таким образом, Cit⁺ — это не постепенное улучшение уже существующего признака, а качественный скачок, требующий определённой внутренней структуры системы.

Рассматриваемая система функционирует в изолированной среде, что принципиально исключает возможность появления нового сигнала за счёт внешнего источника. Все входные компоненты, включая Cit, изначально присутствуют в питательном растворе и на протяжении эксперимента не изменяют внешний контекст системы. Следовательно, любые наблюдаемые изменения в структуре сигналов или распределении состояний не могут быть объяснены притоком новой информации извне.

В рамках ранговой теории это означает, что динамика системы определяется исключительно внутренними механизмами — в частности, локальной регуляризацией и перераспределением устойчивостей внутри пространства состояний.

13.3 Вырожденная группа как симметричная область пространства состояний

До перехода система характеризуется наличием вырожденной группы состояний, для которых ранговая функция не различает элементы. Эта группа является симметричной: внутри неё отсутствуют устойчивые асимметрии, а соответствующее распределение не выделяет предпочтительных направлений динамики.

Важно подчеркнуть, что вырожденная группа не является отдельным уровнем иерархии рангового пространства и не соответствует переходу к уровню k+1. Она представляет собой симметричную область внутри исходного пространства сигналов, в которой отсутствует различение по рангу.

13.4 Роль локальной регуляризации H

Поскольку внешний контекст фиксирован, единственным источником структурных изменений выступает локальная регуляризация H. Она не добавляет новый сигнал и не вводит дополнительную информацию, но изменяет устойчивость траекторий и допустимых состояний внутри вырожденной группы.

Регуляризация нарушает симметрию, делая некоторые направления динамики устойчивыми, а другие — неустойчивыми. При этом Cit не выступает как внешний фактор, а играет роль внутреннего компонента входного сигнала, который становится различимым только после изменения локальной структуры устойчивостей.

13.5. Разрушение симметрии и возникновение нового типа сигнала

Под действием регуляризации симметрия вырожденной группы разрушается, и внутри неё формируются устойчивые асимметрии. Эти асимметрии не являются уточнением существующей иерархии исходного рангового пространства, а соответствуют возникновению нового типа различения состояний.

Таким образом, система начинает выделять новый тип сигнала, связанный с Cit, который ранее не был представлен в форме устойчивой ранговой структуры. Это различение не может быть сведено к переходу на более высокий уровень иерархии исходного пространства, поскольку меняется сама семантика ранговой функции.

13.6 Формирование нового рангового пространства

Возникшие устойчивые асимметрии индуцируют новое ранговое пространство, определённое на подмножестве состояний, ранее входивших в вырожденную группу. Это пространство обладает собственной ранговой функцией, собственной метрикой доминирования и собственной иерархией уровней структуры.

Таким образом, переход, наблюдаемый в эксперименте с Cit, следует интерпретировать не как усложнение иерархии исходного рангового пространства, а как формирование нового рангового пространства внутри симметричной области, вызванное локальной регуляризацией в изолированной среде.

13.7. Интерпретация в терминах ранговой теории

С точки зрения ранговой теории данный механизм демонстрирует, что в изолированной системе появление нового типа сигнала возможно без притока внешней информации, исключительно за счёт разрушения симметрии во вырожденных группах. Вырожденная группа выступает не как уровень иерархии, а как источник потенциальных новых ранговых пространств, которые актуализируются при изменении локальных условий устойчивости.

Эксперимент с Cit⁺ демонстрирует, что новые сигнальные пространства могут возникать без изменения внешнего входа, исключительно за счёт локальной регуляризации и накопления латентной вариативности внутри вырожденных групп рангового пространства.

14. Иерархия ранговых и марковских пространств: симметрия, регуляризация и формирование структуры

14.1. От входного сигнала к ранговому пространству

Пусть система наблюдает входной сигнал X, представляющий собой последовательность состояний или символов. Накопление статистики по X приводит к формированию маргинальных вероятностей появления элементов. Эти маргинальные вероятности создают ранговое пространство, в котором элементы упорядочены по устойчивым различиям частот.

Согласно Теоремам R.1–R.4, оптимальное распределение в ранговом пространстве имеет вид

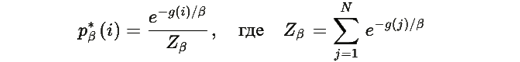
где функция ранговой стоимости g(i) кодирует устойчивую асимметрию элементов. Ранговое пространство, таким образом, фиксирует структурные различия, сохраняющиеся при допустимых возмущениях.

Принципиально важно, что ранговое пространство неизбежно содержит два типа объектов:

1. устойчивые асимметрии — уникальные ранги;
2. вырожденные группы — множества элементов с равными или статистически неразличимыми маргинальными вероятностями. Они характеризуются симметрией и неопределённостью.

Вырожденные группы обладают симметрией и повышенной энтропией и не допускают дальнейшего структурного разрешения на уровне маргинальных вероятностей. Принципиально важно, что вырожденные группы не являются шумом. Они представляют собой области потенциальной структуры, неразрешимой в рамках текущего уровня описания.

14.2. Марковское пространство как динамика внутри рангов

На основе рангового пространства строится марковское пространство условных вероятностей. Допустимые переходы между элементами определяются структурой ранговой стоимости g(i), а сами переходы задаются условными вероятностями

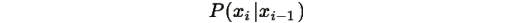
что формирует цепь Маркова внутри рангового пространства.

Теоремы 7.3.1–7.3.2 показывают, что при кусочно-линейной структуре g(i) условные вероятности обладают кусочной структурой и разбиваются на характерные области. Таким образом, марковская динамика наследует геометрию рангового пространства, но не добавляет новых различий между элементами.

14.3. Предсказание и регуляризация: роль функционала H

Каждый уровень марковской иерархии формирует предсказание Y(t) для входного сигнала. Регуляризующий функционал H(t)=X(t)−Y(t) не является ошибкой в смысле Predictive Coding. Он представляет собой контекстное воздействие, связанное с альтернативными устойчивыми траекториями марковской динамики.

Регуляризация H обладает следующими свойствами:

• не создаёт новых состояний;
• не задаёт динамику напрямую;
• действует на устойчивость траекторий;
• изменяет относительную энтропийную и энергетическую стоимость переходов.

Воздействие регуляризации реализуется через модификацию входного сигнала: X(t+1) ↦ X(t+1)⋅H(t), что приводит к асимметричному воздействию на элементы, ранее принадлежавшие одной вырожденной группе.

Таким образом, H осуществляет обратную связь от марковского пространства к ранговому, не разрушая его структуры, но изменяя устойчивость элементов внутри допустимых областей.

14.4. Разрушение симметрии в вырожденных группах

Вырожденные группы являются единственными областями, где возможно структурное развитие. Под действием регуляризации H элементы вырожденной группы начинают получать контекстно-различимые воздействия, если во входных данных присутствует латентная структура.

Важно подчеркнуть, что разрушение симметрии:

• не является мгновенным;
• требует накопления статистики;
• возможно только при устойчивости асимметрий во времени.

Если асимметрии, индуцированные регуляризацией, сохраняются на временах, превышающих характерное время релаксации (см. Теорему S.4), они перестают быть флуктуациями и приобретают статус устойчивых различий.

14.5. Формирование вложенного рангового пространства

При устойчивом разрушении симметрии внутри вырожденной группы формируется вложенное ранговое пространство, определяемое новыми маргинальными вероятностями элементов группы. Это ранговое пространство:

• наследует ограничения родительского уровня;
• обладает собственной функцией ранговой стоимости;
• отражает асимметрию, возникшую за счёт контекста H.

Существенно, что:

• устойчивые ранги не порождают новых ранговых пространств;
• только вырожденные группы обладают потенциалом структурного усложнения.

После формирования вложенного рангового пространства становится возможным построение марковского пространства второго порядка — цепей условных вероятностей внутри бывшей вырожденной группы, но уже вокруг сигнала типа X+H.

14.6 Связь с Марковскими одеялами

В контексте данной конструкции Марковское одеяло интерпретируется как структурная граница, ограничивающая каналы взаимодействия между вложенными ранговыми пространствами. Формирование нового рангового пространства внутри вырожденной группы сопровождается функциональной изоляцией соответствующей динамики, что эквивалентно возникновению дочернего Марковского одеяла.

Таким образом, иерархия ранговых и марковских пространств естественным образом согласуется с иерархией Марковских одеял, дополняя её вариационным описанием процессов симметрии, асимметрии и структурного роста.

Из изложенного следует фундаментальный результат ранговой теории:

Вырожденные симметричные группы являются единственным источником формирования новых ранговых пространств.

Ранговая теория, таким образом, описывает не механизм порождения состояний, а механизм балансировки, отбора и иерархического структурирования системы в условиях ограниченных ресурсов.

Марковская динамика реализует движение внутри структуры, а регуляризация определяет, какие траектории и какие симметрии могут быть устойчиво разрушены.