Сегодня поговорим про сферу Римана
@mat2hubЧто это вообще такое?
Как бы это странно ни звучало, сфера Римана названа в честь немецкого математика Бернхарда Римана. Служит она для представления бесконечно удаленной от центра координат точки на комплексной поверхности.
И как это работает?
Во-первых, необходимо напомнить, что такое комплексное число. Оно состоит из действительной и мнимой части и записывается как:
z=x+iy ,
где i= √-1 есть ни что иное, как мнимая единица. Число, которое не существует на множестве вещественных чисел. А сам y вместе с x как раз принадлежат множеству существенных чисел.
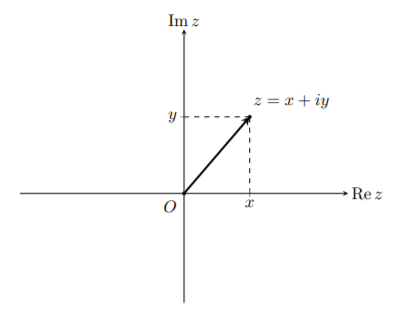
Как можно понять по записи, комплексное число можно представить на Декартовых координатах. Будет оно иметь вид радиус-вектора (вектор, начинающийся в точке (0, 0) ) в точке (x,y).
И все же, что за сфера Римана?
В основе действия лежит элементарная геометрия.
Представим Евклидово трехмерное пространство с координатами (ξ, η, θ) и совместим комплексную плоскость C с плоскостью Oξη так, чтобы действительная ось (Ox) совпала с осью Oξ, а мнимая ось (Oy) с осью Oη, и положительные направления соответствующих осей совпадали.
В пространстве изобразим сферу с радусом R= 0.5 и центром в
точке (0, 0, 0.5). Уравнение сферы имеет вид:
ξ² + η² + (θ – ½ )² = 1/4 ,
Точка P (0, 0, 1) будет называться полюсом сферы.
Теперь соеденим точки P (0, 0, 1) и Z (x,y). Отрезок PZ пересекает сферу только в одной точке M. Для удобства координаты точки М будут
взяты (ξ, η, θ). Точка M(ξ, η, θ) называется стереографической проекцией точки z на сферу.

Стереографическая проекция устанавливает взаимно однозначное соответствие между точками комплексной плоскости C и точками сферы с выколотым полюсом P.
В силу колинеарности точек P(0, 0, 1), M(ξ, η, θ) и z(x, y, 0) имеем
ξ/x = η/y = (1 - θ)/1 ,
откуда выводим
x = ξ/(1 - θ) , y = η/(1 - θ) , z = (ξ + iη)/(1 - θ) .
Поскольку
|z|² = (ξ² + η²)/(1 - θ)² ,
то из уравнения сферы получаем
|z|² = θ/(1 - θ) .
Из имеющихся уравнений можно найти так называемы формулы стереографической проекции (уравнения для ξ,η,θ):
ξ = x/(1+ |z|²); η = y/(1+ |z|²) ; θ = |z|²/(1+ |z|²).
Добавим к комплексной плоскости C идеальный объект, называемый бесконечно удаленной точкой и обозначаемый символом ∞. Комплексную плоскость с присоединенной к ней бесконечно удаленной точкой называют расширенной комплексной плоскостью и обозначать символом C, т.е. C = C ∪ {∞}.
Когда комплексное число z стремится к бесконечно удаленной точке, то образ этой точки стремиться к полюсу P.