Рождественская теорема Ферма

Любое простое число p = 4k + 1 представимо в виде суммы квадратов двух натуральных чисел.
Это утверждение стало известным из письма П.Ферма М.Мерсенну (который был основателем научного кружка и как бы посредником в кругу самых знаменитых учёных Европы), датированного 25 декабря 1640 г. — ровно 383 года назад. Ферма сообщил, что доказал эту удивительную теорему (но в письме ему, как обычно, не хватило места на полях, чтобы привести само доказательство 😊).
Первое доказательство теоремы было опубликовано Л.Эйлером в 1742 г., оно использовало метод бесконечного спуска. Позже было найдено много других доказательств, основанных на разных идеях; их дали Ж.Лагранж, К.Гаусс, Г.Минковский, и многие другие учёные — понимание всех этих доказательств требует весьма серьёзной математической подготовки.
В 1990 г. Доном Цагиром было получено ещё одно оригинальное доказательство теоремы, также не слишком простое для непрофессионального математика. Но в 2007 г. А.В. Спиваку, лектору Малого мехмата МГУ, удалось придумать очень простую и красивую его визуализацию на клетчатой бумаге — с помощью «ветряных мельниц», или «крылатых квадратов». Хорошее изложение этого материала сделал Mathologer.
Рассмотрим это элементарное доказательство.
Очевидно, что если простое число p = 4k + 1 можно записать как сумму двух целых квадратов, то один из этих квадратов должен быть нечётным числом, а другой — чётным:
p = x² + (2y)² = x² + 4y².
Оказывается, имеет смысл несколько расширить задачу, заменив одну из букв y в формуле на z:
p = x² + 4yz
— это в итоге даст большее пространство для манёвра и позволит найти простую формализацию решения.
Теперь можно заметить, что полученное выражение совпадает с видом числа
p = 1 + 4k, если выбрать x = 1, y = 1, z = k.
Помимо основного решения (x; y; z) = (1; 1; k) наше уравнение
p = x² + 4yz допускает множество других решений, и для любого конкретного простого числа p эти другие решения также легко найти.
Рассмотрим на примере:
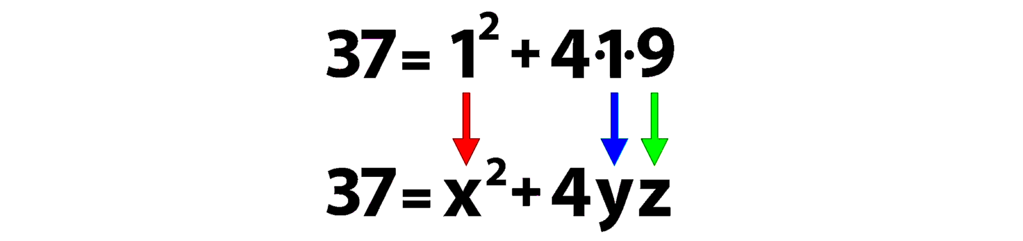
Основное решение: (1; 1; 9). А вот остальные решения:
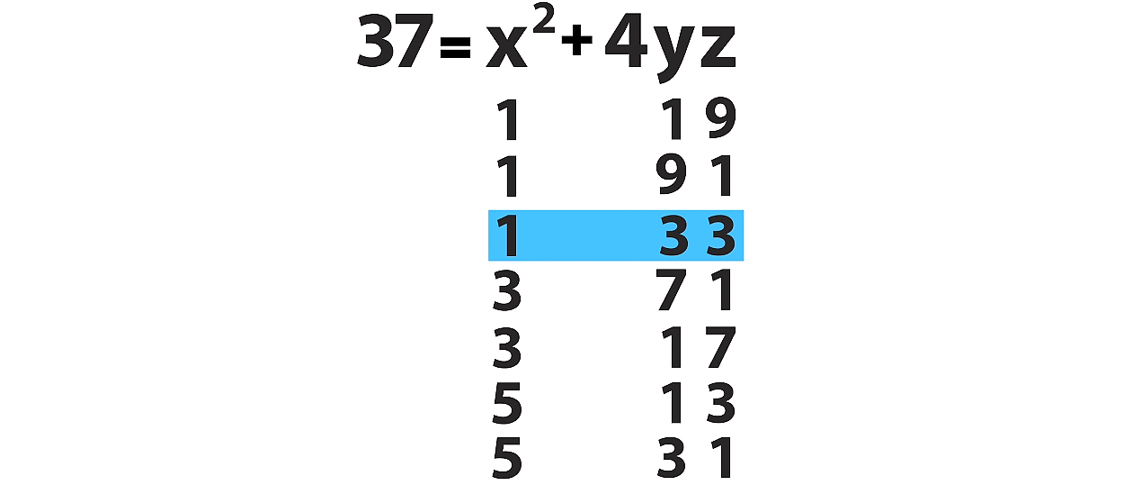
В действительности, нас интересует только то решение, для которого y = z, поскольку именно оно преобразуется обратно в решение исходного уравнения — в способ записи простого числа в сумму квадратов, вот так:
37 = x² + 4y² = x² + (2y)² = 1² + (2·3)² = 1² + 6².
Самое главное наблюдение, которое нужно совершить (и затем его доказать!), состоит в том, что наше уравнение p = x² + 4yz имеет всегда нечётное количество решений. При этом важно заметить, что если мы нашли какое-нибудь решение (x; y; z), то и (x; z; y) тоже непременно будет решением, поскольку уравнение инвариантно относительно замены y ↔ z. Таким образом, все решения разбиваются на пары; но поскольку их нечётное количество, то непременно будет решение, которому нет пары (если угодно, которое само себе образует пару) — это решение, для которого y = z.
Итак, грядущее волшебство и поистине рождественское чудо состоит в изящнейшем геометрическом способе увидеть это нечётное количество решений.
Рассмотрим на примере какое-нибудь решение.
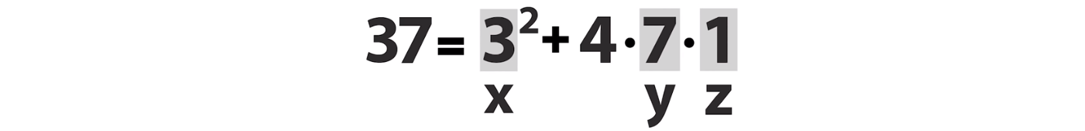
Здесь 3² — это площадь квадрата со стороной 3, а 4·7·1 — площадь четырёх прямоугольников со сторонами 7 и 1.
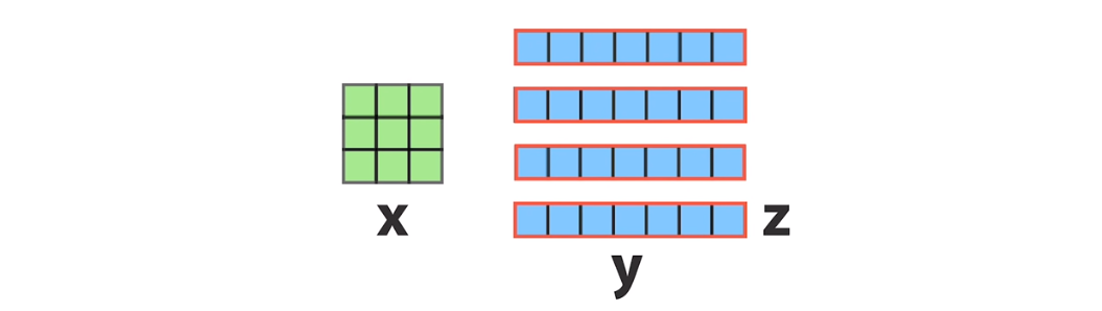
Красивый и симметричный способ расположения этих фигур — это ветряная мельница. Именно эту конструкцию будем считать интерпретацией решения нашего уравнения:
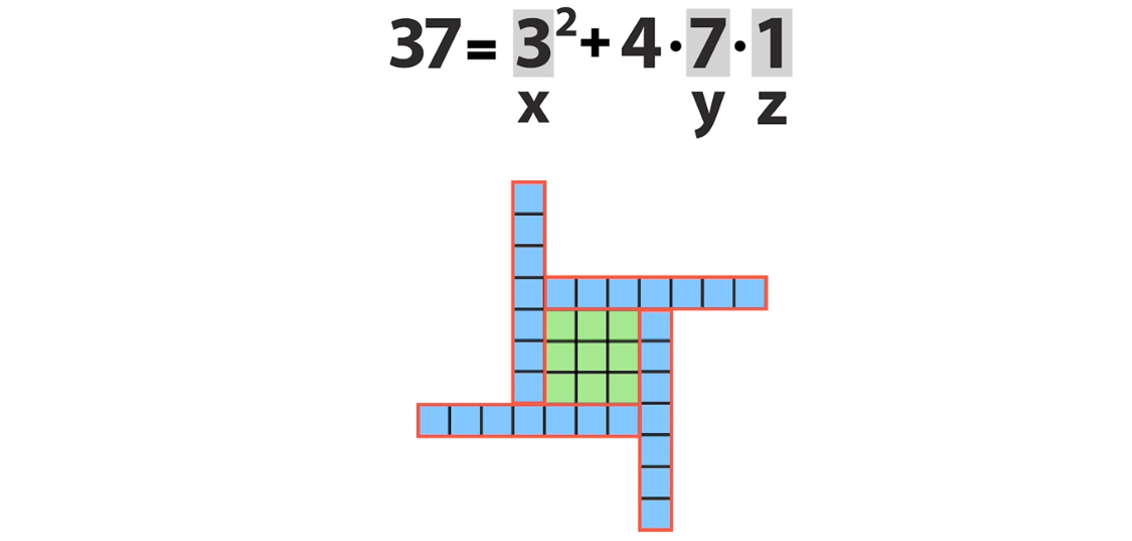
Поменяв местами y и z, получим другую мельницу, соответствующую другому решению:
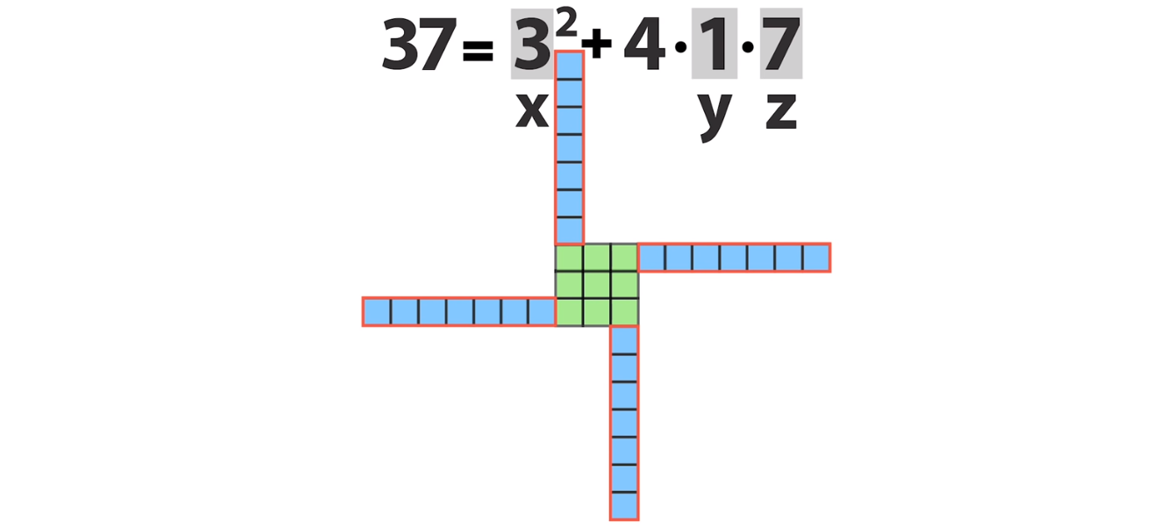
Всего для данного уравнения мы имеем три пары решений и ещё одно решение, не имеющее пары:
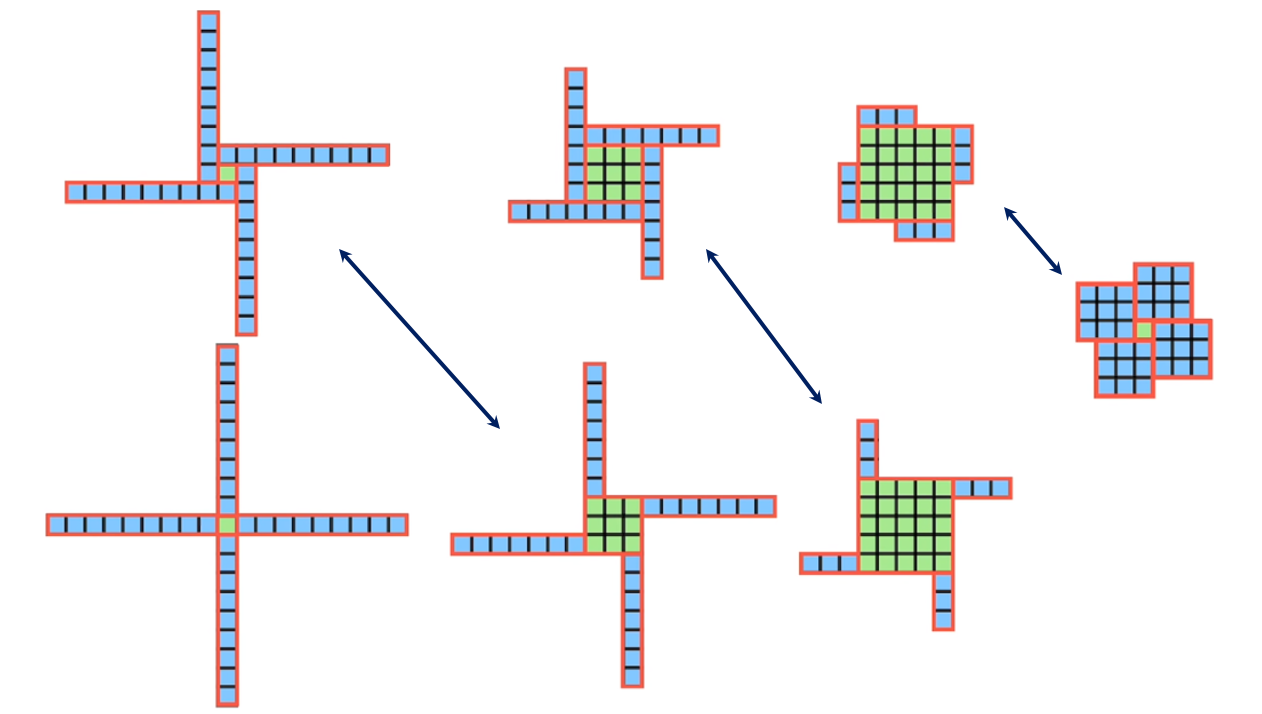
А теперь само волшебство! Как, например, в решении 37 = 3² + 4·7·1 увидеть ещё одно решение — а именно, 37 = 5² + 4·1·3?
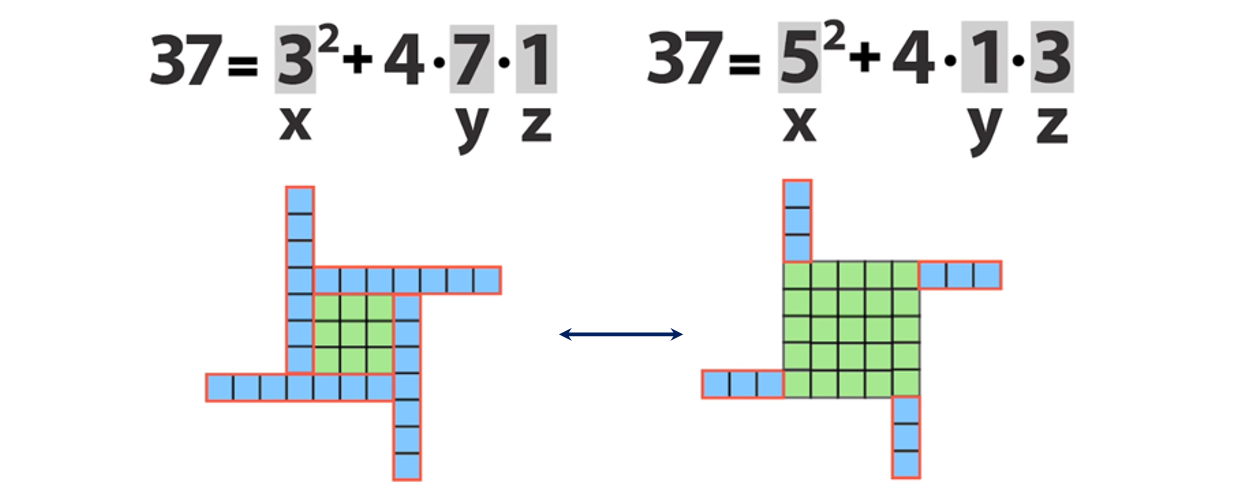
Глядя на любую мельницу, имеющую зелёное ядро, мы получим вторую ветряную мельницу — второе решение, разрезав середину вдоль лопастей мельницы, вот так:
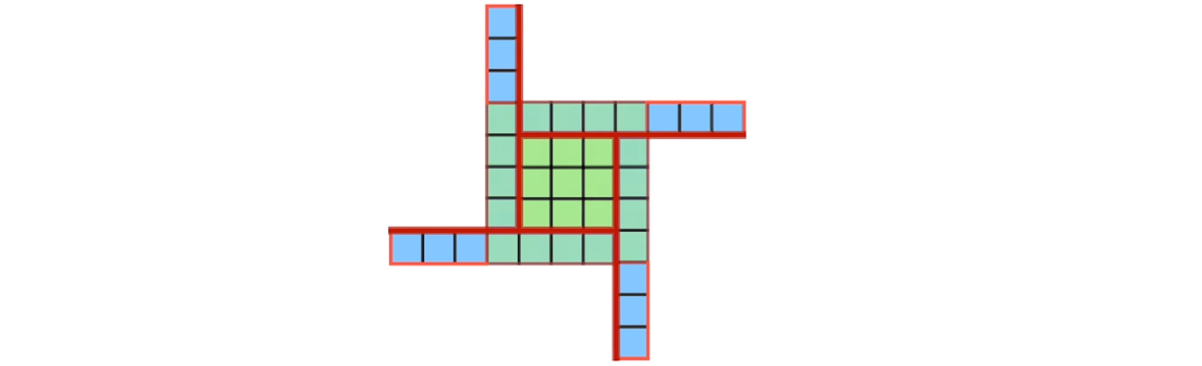
Это новое решение и исходное решение связаны тем, что их ветряные мельницы имеют одинаковые контуры очертания.
Классификация их по контурам очертания даёт ещё один способ разбиения на пары. Единственным исключением теперь является контур очертания мельницы с прямым крестом, который встречается только один раз. Все остальные ветряные мельницы идут совпадающими парами. Для того чтобы убедиться в этом, нужно проделать несложную работу — отметить все случаи того, как прямоугольные лопасти могут располагаться вокруг квадратного сердечника. Очевидно, что очертание прямо-крестовой ветряной мельницы встречается только один раз и всегда существует хотя бы одна такая прямо-крестовая мельница, соответствующая основному решению.
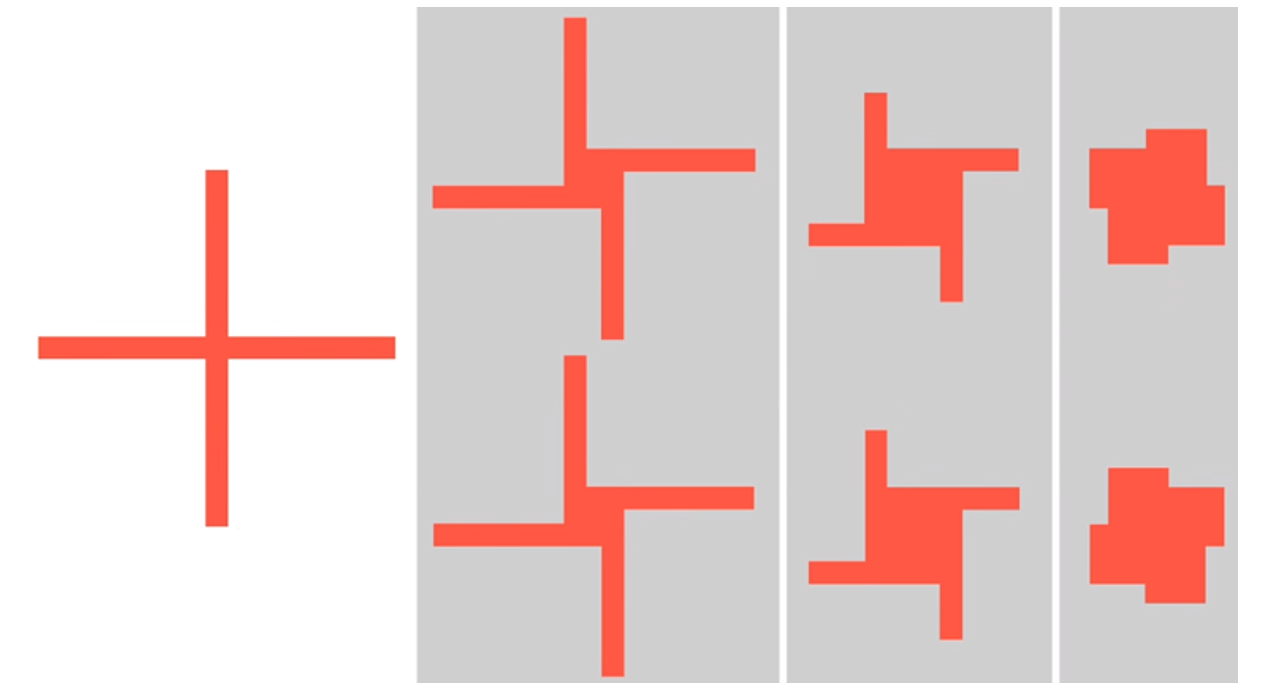
Ещё необходимо учесть, что в целом таких прямых крестов может оказаться несколько.
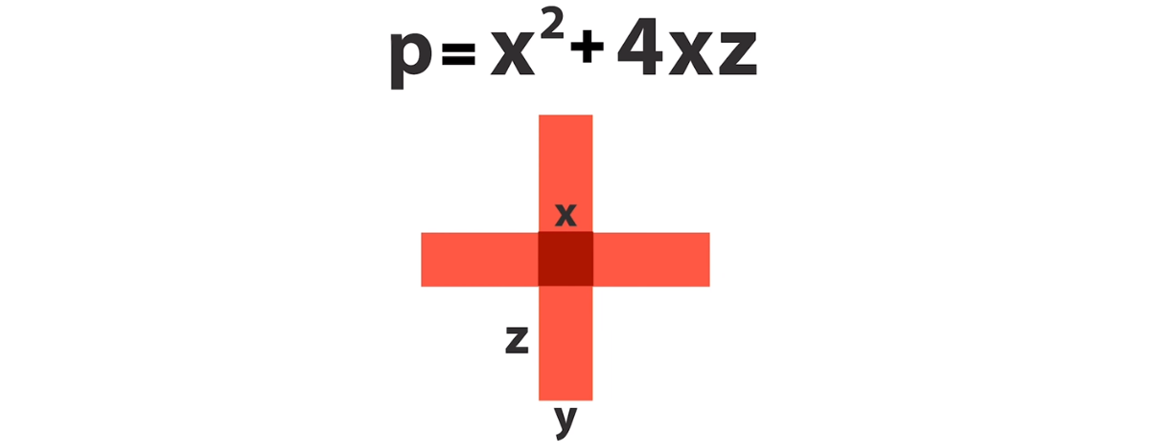
В этом случае длина стороны квадрата x равна длине стороны y одного из прямоугольников. Это означает, что мы можем заменить y на x и вытащить его за скобку: p = x (x + 4z).
Таким образом, в случае прямого креста число p является произведением двух целых чисел. Но поскольку p простое, оно имеет только два делителя — 1 и само число p, поэтому ясно, что меньший множитель x должен быть равен 1. Но для прямого креста y = x, и потому можно заключить, что для каждого простого числа p = 4k + 1 существует только один прямой крест, соответствующий основному решению (1; 1; k).
Поскольку, как мы помним, все остальные — закрученные — кресты встречаются парами, то общее количество решений будет равно чётному числу плюс один, т.е. нечётному числу. Этот вывод завершает доказательство рождественской теоремы Ферма.