Решение. Честная игра с «нечестной» монетой (#13)

Например, можно придумать такую игру:

Обозначим 0 = «орёл», 1 = «решка». Пусть 0 выпадает с вероятностью p, 1 – с вероятностью 1-p. Рассмотрим множество исходов после двух бросков монеты: 00, 01, 10, 11. Заметим, что исходы 01 и 10 равновероятны

Эта пара равновероятных событий служит базой для составления справедливой игры.

Для двух игроков А и Д организуем игру следующим образом. Делаем два броска, после чего смотрим на выпавшую последовательность

01 – выиграл игрок A, вероятность = p(1-p)

10 – выиграл игрок Д, вероятность = p(1-p)

00 или 11 – никто не выиграл, вероятность 1 - 2p(1-p)

В случае, если после первых двух бросков никто не выиграл, повторяем упражнение. Делаем два новых броска. Если на втором шаге опять нет выигравших, то продолжаем. И так далее до тех пор, пока не выпадет выигрывающая последовательность. Так как на каждом новом шаге вероятности выигрыша у игроков А и Д совпадают, то интуитивно понятно, что

Покажем это явно. Обозначим q = 1-2p(1-p), то есть это вероятность того, что на отдельно взятом шаге нет победителя. Тогда вероятность того, что игрок выиграет ровно на шаге n, равна

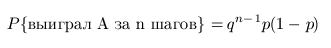
Просуммируем по n

Сумма геометрической прогрессии равна 1/1-q, следовательно,

Справедливость игры доказана.